
Izmeritelnye_preobrazovateli_Mironov
.pdfКлассический метод анализа При классическом методе анализа дифференциального уравнения (10.5)
решение имеет вид
θ(t) = θn(t)+θy(t) |
(10.6) |
где θn(t) – характеризует переходный режим (общее решение); θy(t) – характеризует установившийся режим (частное решение).
Общее решение исследуемого дифференциального уравнения (10.5) находится из однородного уравнения (10.7), на основе которого составляется ха-
рактеристическое уравнение (10.8), имеющее корень λ (10.9). |
|
|||
T·λ+1 = 0 |
(10.8) |
|||
λ = − |
1 |
|
(10.9) |
|
T |
||||
|
|
|||
В данном случае характеристическое уравнение имеет один вещественный корень, и соответственно θn(t) имеет вид
θn (t) = B eλt = B e−t /T |
(10.10) |
где B – постоянная интегрирования.
Значение θy(t) определяется видом правой части исходного уравнения (10.5). При постоянной правой части (что имеет место в рассматриваемом слу-
чае) θy(t) – тоже постоянная величина: |
|
|
|
|||||
|
|
|
θy(t) = С |
|
|
(10.11) |
||
Таким образом, θ(t) и θ&(t) запишутся в виде |
|
|||||||
|
|
θ(t) = B e−t /T |
+C |
(10.12) |
||||
|
θ&(t) = − |
1 |
B e−t /T +0 |
(10.13) |
||||
|
|
|||||||
|
|
|
|
T |
|
|
|
|
Подставляя значения θ(t) и θ&(t) в (10.7), получим |
|
|||||||
|
1 |
|
−t /T |
−t /T |
|
|
||
T − |
|
B e |
|
+ B e |
|
+C = θ0 |
|
|
T |
|
|
|
|||||
|
|
|
|
|
|
|
||
или
−B e−t /T + B e−t /T +C = θ0
191
После приведения подобных (в последнем соотношении) определяется значение C = θ0 .
Подставляя значение C = θ0 в (10.12), получим
θ(t) = B e−t /T +θ0 .
Для нахождения постоянной интегрирования «B» воспользуемся началь-
ными условиями (при t = 0 θ(t) = 0).
0 = B·e0+θ0.
Учитывая, что e0 = 1, находим, что постоянная интегрирования B = –θ0. Итак, окончательно решение дифференциального уравнения (10.5) запи-
шется в виде
θ(t) = −θ0 e−t /T +θ0 = θ0 (1−e−t /T ) . |
(10.14) |
Таким образом, при скачкообразном изменении температуры окружающей среды температура датчика изменяется по экспоненциальному закону. График зависимости θ = f(t) в соответствии с выражением (10.14) приведен на рис. 10.3.
Отметим, что с погрешностью ±5 % переходный процесс заканчивается за время, равное трем постоянным времени датчика T, т. е. через t = 3T можно считать, что с указанной погрешностью температура датчика становится равной температуре окружающей среды.
За время t = 5T переходный процесс заканчивается с погрешностью ±1 %. Другими словами, за время 3T проходит 95 % переходного процесса, а за
время 5T проходит 99 % переходного процесса.
Таким образом, постоянная времени T характеризует тепловую инерционность датчика. При больших Т датчик медленно реагирует на изменения температуры окружающей среды, а при малых Т датчик быстро «отрабатывает» изменения температуры.
В паспортных данных датчиков обычно приводятся значения не постоянной времени Т, а значения близкой к ней величины, называемой «показатель тепловой инерции (ПТИ)». ПТИ по определению – это время, необходимое для
192
того, чтобы при внесении датчика в среду с постоянной температурой разность температур среды и любой точки внесенного в нее датчика стала равной 0,37 того значения, которое она имела бы в момент наступления регулярного теплового режима [51].
Различают датчики малоинерционные (ПТИ<10 секунд), датчики средней инерционности (ПТИ от 10 до 60 секунд) и датчики большой инерционности (ПТИ>60 секунд).
Метод определения показателя тепловой инерции изложен в литературе (см., например, [27]) и в настоящем учебном пособии не рассматривается. Значения показателя тепловой инерции для различных типов датчиков приведены, например, в справочнике [37].
Операторный метод анализа При операторном методе решения дифференциального уравнения (10.5)
необходимо его представить в виде операторного изображения, используя для этого преобразование Лапласа (подробней см. в литературе [29–32]):
T·[p·θ(p)–θ(0)]+θ(p) = θ0/p |
(10.15) |
где θ(p) – изображение по Лапласу оригинала θ(t);
θ(0) – значение θ(t) при t = 0.
Начальные условия для рассматриваемого уравнения сформулированы выше (отметим, что при t = 0 θ(0) = 0; θс(0) = θ0.
Решая уравнение (10.15) относительно θ(p) с учетом начальных условий, получим
θ( p) = |
θ0 |
|
(10.16) |
|
p(Tp |
+1) |
|||
|
|
Для перехода от изображения θ(p) к оригиналу θ(t) воспользуемся данными табл. 10.1.
193
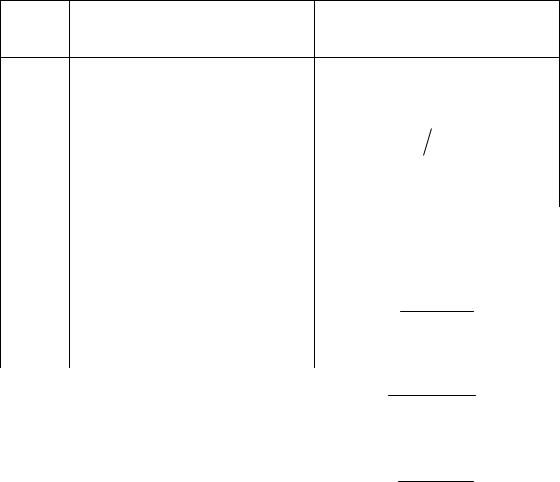
Таблица 10.1
Значения оригиналов и их изображений по Лапласу
№ п/п |
Оригинал |
Изображение |
|
|
|
1 |
2 |
3 |
1 |
|
|
|
|
A |
|
|
|
|
A |
|||
|
|
|
|
|
|
|
|
p |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
t |
|
|
|
1 p2 |
||||
3 |
|
|
|
f (t) |
|
|
F(p) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
e |
−αt |
|
|
1 |
|
|
|||
|
|
|
|
|
p +α |
||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t e−αt |
1 |
|
|
||||||
6 |
|
|
|
(p +α)2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
t |
− |
1 |
|
+ |
e−αt |
1 |
|
|
|||
7 |
|
|
|
|
α2 |
p2 (p +α) |
|||||||
α |
α2 |
||||||||||||
|
|
|
|
|
|
|
−αt |
|
α |
||||
5 |
|
|
1−e |
p(p +α) |
|||||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для приведения выражения (10.16) к табличному виду разделим числитель и знаменатель этого выражения на величину Т. При этом равенство (10.16) принимает вид
θ( p) = θ0 |
1/ T |
(10.17) |
|
p( p +1/ T ) |
|||
|
|
Выражение (10.17) соответствует табличному значению изображения, приведенного в таблице под номером «5» (при a =1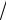 T ).
T ).
Тогда в соответствии с таблицей оригинал изображения (10.17) запишется в виде
θ(t) = θ0 (1−e−t /T ). |
(10.18) |
194 |
|
Выражение (10.18) полностью совпадает с выражением (10.14), которое получено классическим методом. Соответственно полностью правомерны выводы по результатам решения дифференциального уравнения (10.5), сделанные выше.
10.3. Линейное изменение температуры
Начальные условия При линейном изменении температуры окружающей среды, окружающей
датчик (рис. 10.4), исследуемое дифференциальное уравнение (10.4) принимает следуюший вид:
T θ&(t) +θ(t) = θ0 +b t |
(10.19) |
где b – коэффициент, характеризующий скорость линейного изменения температуры окружающей среды.
Рис. 10.4. Графики зависимостей θс(t) и θ(t) при линейном изменении температуры окружающей среды: θс(t) – температура окружающей среды; θ(t) – температура датчика
Начальные условия в рассматриваемом случае запишутся для t = 0 θ(t) = 0, θc = θ0
Классический метод анализа При классическом методе анализа дифференциального уравнения (10.19)
остаются в силе положения, изложенные выше. Величины θn(t) и θy(t) при этом принимают вид
θn (t) = B e−t /T , |
(10/20) |
θy (t) = C + D t , |
(10.21) |
195 |
|

где B – постоянная интегрирования; |
|
|
|
|
|
||||
C и D – постоянные коэффициенты. |
|
|
|
|
|
||||
Соответственно θ(t) и θ&(t) |
и запишутся в виде |
|
|
|
|||||
|
|
θ(t) = B e−t /T +C + D t , |
|
|
(10.22) |
||||
|
|
θ&(t) = − |
1 |
|
B e−t /T + D . |
|
|
(10.23) |
|
|
|
T |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
Подставляя значения θ(t) и θ&(t) |
в исходное дифференциальное уравнение |
||||||||
(10.19), получим |
|
|
|
|
|
|
|
|
|
|
1 |
− t |
|
|
− t |
|
|
|
|
T − |
|
B e T + D + B |
|
e T + C + D t =θ0 |
+b t |
. |
(10.24) |
||
T |
|
||||||||
|
|
|
|
|
|
||||
Раскрыв скобки и выполнив приведение подобных, приводим выражение
(10.24) к виду
T D + C + D t =θ0 + b t . |
(10.25) |
|
Уравнение (10.25) правомерно, если равны коэффициенты при перемен- |
||
ной величине t, имеющей равные степени. |
|
|
Отсюда получим: |
|
|
для t0 |
T·D+C = θ0, |
(10.26) |
для t1 |
D =b. |
(10.27) |
Совместное решение уравнений (10.26) и (10.27) дает значение коэффи- |
||
циента С: |
|
|
|
C = θ0–b·T |
(10.28) |
Подставляя значения коэффициентов D и C в уравнение (10.28), получим |
||
θ(t) = B e−t /T +θ0 −b T +b t . |
(10.29) |
|
Для определения постоянной интегрирования B воспользуемся началь- |
||
ными условиями (при t = 0 θ(0)=θ0 ): |
|
|
θ0 |
= B e0 +θ0 −b T +b 0 , |
(10.30) |
откуда получаем |
|
|
|
B = b T . |
(10.31) |
|
196 |
|

В окончательном виде температура датчика запишется в виде |
|
θ(t) = θ0 +b t −b T (1−e−t /T ) . |
(10.32) |
График зависимости θ = f(t) для рассматриваемого случая приведен на рис. 10.4.
Приведенный анализ позволяет сделать следующие выводы:
1)при линейном изменении температуры окружающей среды темпера-
тура датчика не равна этой температуре даже после окончания переходного процесса (при t →∞);
2)температура датчика меньше температуры окружающей среды на величину b T , где b – коэффициент, характеризующий скорость изменения температуры среды, а T – постоянная времени датчика, характеризующая его тепловую инерцию;
3)динамическая погрешность при измерении линейно изменяющейся температуры окружающей среды датчиком с постоянной времени T растет с ростом величин «b» и «Т» и уменьшается при уменьшении величин «b» и «Т».
Операторный метод анализа В операторной форме уравнение (10.19) принимает вид
T [p θ( p) −θ(0)]+θ(p)=θ0 / p +b / p2 , |
(10.33) |
где θ(p) – изображение по Лапласу оригинала θ(t); θ(0) – значение θ(t) при t = 0.
Начальные условия в рассматриваемом случае сформулированы выше
(отметим, что при t = 0 θ(t) = θ0; т. е. θ(0) = θ0).
Решая уравнение (10.33) относительно θ(p) с учетом начальных условий, получим
θ(p) = b + p θ0 + p2 θ0 T p2 (Tp +1)
или
θ(p) = |
b |
+ |
θ0 |
|
+ |
|
θ0 T |
|
|
p2 (Tp +1) |
Tp +1 |
Tp +1 |
|||||||
|
|
|
|||||||
(10.34)
(10.35)
197
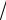
Для приведения выражения (10.35) к табличному виду (см. табл. 10.1) разделим числитель и знаменатель этого выражения на величину Т.
После деления на величину Т и проведения необходимых преобразований выражение (10.35) примет вид
θ(p) = |
b |
|
|
|
1 |
+θ0 |
1/ T |
+θ0 |
1 |
(10.36) |
|
p |
2 |
( p +1/ T ) |
p( p +1/ T ) |
p +1/ T |
|||||
|
T |
|
|
|
|
|||||
Первый член выражения (10.36) соответствует изображению, приведенному в табл. 10.1 под номером 7, второй – под номером 5 и третий – под номе-
ром 4 (при a =1 T ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Оригинал изображения (10.36) имеет вид |
|
|
|
|||||||||||
θ(t) = |
b |
|
t |
|
1 |
|
e |
−t /T |
|
|
(1−e−t /T ) +θ0 |
e−t /T |
|
|
|
− |
+ |
|
|
|
+θ0 |
(10.37) |
|||||||
T |
1/ T |
2 |
|
|
2 |
|||||||||
|
|
|
1/ T 1/ T |
|
|
|
|
|
|
|||||
Раскрыв скобки и выполнив приведение подобных, окончательно полу-
чим
θ(t) = θ0 +b t −bT (1−e−t /T ) |
(10.38) |
Выражение (10.38) целиком совпадает с выражением (10.32), полученным при анализе исследуемого дифференциального уравнения классическим методом. Соответственно полностью правомерны выводы, сделанные выше и для рассматриваемого случая при анализе дифференциального уравнения (10.19) операторным методом.
198
11.МОСТОВЫЕ ИЗМЕРИТЕЛЬНЫЕ СХЕМЫ
11.1.Общие положения
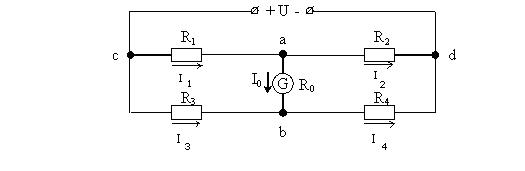
В данной главе рассмотрены основные соотношения и терминология, используемые при анализе четырехплечих мостовых измерительных схем постоянного тока (рис. 11.1).
Рис. 11.1. Принципиальная электрическая схема четырехплечего измерительного моста: U – напряжение источника питания; G – измерительный прибор (например, микроамперметр магнитоэлектрической системы); a–b – измерительная диагональ; c–d – питающая диагональ; c–a – первое, a–d – второе, c–b – третье, b–d – четвертое плечи мостовой схемы; R0 – внутренне сопротивление прибора
визмерительной диагонали; I0 – ток в измерительной диагонали
Врассматриваемом случае сопротивления плеч мостовой измерительной
схемы равны R1, R2, R3, R4.
Ток в измерительной диагонали I0 связан с остальными параметрами мостовой схемы соотношением
I0 |
=U |
|
|
|
|
|
|
R1 R4 |
− R2 R3 |
|
|
|
|
|
|
. |
(11.1) |
||
R |
(R |
+ R |
)(R |
3 |
+R |
) + R R |
(R + R |
) + R R |
(R |
+ R |
) |
||||||||
|
|
|
|
||||||||||||||||
|
|
0 |
1 |
2 |
|
4 |
1 |
2 |
3 |
4 |
3 |
4 |
1 |
4 |
|
|
|
||
Соотношение (11.1) может быть получено путем анализа мостовой измерительной схемы, приведенной на рис. 11.1, одним из методов электротехники (например, с использованием первого и второго законов Кирхгофа). Выражение (11.1) обычно именуют основным соотношением для таковой мостовой измерительной схемы.
При равновесии мостовой схемы ток в измерительной диагонали I0 тождественно равен нулю. Отметим также, что если в момент считывания показа-
199

ний ток I0 = 0, то мостовая схема называется равновесной, а если в момент считывания показаний ток I0 ≠ 0, то мостовая схема называется неравновесной.
Если значение R0 (см. рис. 11.1) во много раз превосходит каждое из сопротивлений плеч моста, то мостовая схема называется потенциальной. Для потенциальных мостовых измерительных схем обычно принимают R0 → ∞, что позволяет считать ток I0 = 0 и в качестве выходной величины рассматривать напряжение на измерительной диагонали U0 .
В этом случае падение напряжения на измерительной диагонали U0 =U ab
запишется в виде
U0 =U ab =U a −Ub ,
где Ua – потенциал точки a ;
Ub – потенциал точки b.
U a = I1 R1 = R1 R1 U+ R2 ,
Ub = I3 R3 = R3 R3 U+ R4 ,
где U , R1 , R2 , R3 , R4 – определены выше.
Подставляя значения Ua и Ub в (11.2), получим
U0 =U R1 (R3 ++R4 ) − R3 (+R1 + R2 ) (R1 R2 ) (R3 R4 )
(11.2)
(11.3)
(11.4)
(11.5)
После раскрытия скобок и приведения подобных выражение (11.5) принимает вид
U0 =U |
R1 R4 |
− R2 R3 |
|
. |
(11.6) |
|||
(R + R |
2 |
)(R + R |
4 |
) |
||||
|
|
|
||||||
|
1 |
3 |
|
|
|
|||
Выражение (11.6) обычно именуют основным соотношением для потенциальной мостовой схемы.
При равновесии потенциальной мостовой схемы напряжение в измерительной диагонали U0 тождественно равно нулю. Отметим также, что если в момент считывания показаний напряжение U0 = 0, то любая мостовая схема на-
200
