
Izmeritelnye_preobrazovateli_Mironov
.pdfЕсли сведения о случайных погрешностях отсутствуют, то суммарная по-
грешность результата измерения приравнивается к неисключенной система-
тической погрешности Θ, найденной с доверительной вероятностью Р.
При наличии сведений о случайных погрешностях суммарная погрешность результата однократного измерения определяется с учетом следующих положений:
1) если Θσ < 0,8 , то неисключенной систематической погрешностью
пренебрегают и принимают = ε, где ε – случайная погрешность с доверительной вероятностью Р;
2) если Θσ > 0,8 , то случайной погрешностью пренебрегают и принимают
=Θ;
3) если 0,8 ≤ Θσ ≤ 8 , то погрешность результата измерения вычисляют по
формуле
= ±K[ |Θ| + |ε| ] ,
где К – коэффициент, зависящий от принятой доверительной вероятности Р. Для доверительной вероятности Р = 0,95 коэффициент К = 0,76; для дове-
рительной вероятности Р = 0,99 коэффициент К = 0,83.
Погрешности, возникающие из-за пренебрежения одной из составляющих погрешности результата измерения при выполнении указанных неравенств, не превышают 15 %.
При симметричной доверительной погрешности результат однократного измерения представляется в форме А; ± ; Р или А± ; Р.
Числовые значения результата измерения должны оканчиваться цифрами того же разряда, что и значение погрешности .
111

7.2.2. Примеры расчета
В качестве примеров рассмотрены три задачи (задача 7.1, задача 7.2 и задача 7.3), отличающиеся друг от друга исходными данными.
Задача 7.1
Условие задачи С помощью универсального цифрового вольтметра измерено напряжение
сети. Результат измерения U = 218,62 В получен на пределе измерения Uк = 1000 В. Класс точности вольтметра 0,5/0,1; нормальные условия эксплуатации:
τ0 = (20 ± 2) °C ; Н0 =0 А/м .
Измерения проведены при τ = +24 ºС и H = 20 А/м, где τ – температура окружающей среды; Н – напряженность внешнего магнитного поля.
Найти абсолютную погрешность результата измерения и записать результат с учетом найденной погрешности.
Решение задачи Дополнительные погрешности использованного вольтметра определяют-
ся соотношениями
Θτ = τ 10−τ0 Θoc , ΘН = 50H Θoc ,
где Θτ – абсолютная дополнительная систематическая погрешность, возни-
кающая при температуре окружающей среды, равной τ ;
Θoc – абсолютная основная систематическая погрешность вольтметра, опреде-
ляемая его классом точности;
ΘH – абсолютная дополнительная систематическая погрешность, возникающая от воздействия на вольтметр магнитного поля Н.
1. Относительная основная систематическая погрешность вольтметра, обусловленная его классом точности:
112

|
U |
k |
|
||
δoc = 0,5 |
+ 0,1 |
|
−1 % , |
||
U |
|||||
|
|
|
|||
|
|
1000 |
|
|
|
δoc = 0,5 |
+ 0,1 |
|
−1 % |
= 0,8574 % . |
|
218,62 |
|||||
|
|
|
|
2.Абсолютная основная систематическая погрешность вольтметра, обусловленная его классом точности:
Θoc = 100U % δoc % ,
Θос = 218,100%62 0,8574% =1,8743 В
3.Абсолютная дополнительная погрешность, обусловленная воздействием температуры:
Θτ = 2410−22 1,8743=0,3749 В
4.Абсолютная дополнительная погрешность, обусловленная воздействием магнитного поля:
ΘН = 5020 1,8743=0,7497 В
5.Суммарная абсолютная систематическая погрешность вольтметра Θ определяется соотношением
|
m |
|
Θ = k |
∑Θ2j , |
|
|
j=1 |
|
где k =1,1для доверительной вероятности P = 0,95 ; |
|
|
Θ j – j-я составляющая погрешности. |
|
|
Θ =1,1 Θoc2 |
+ Θτ2 + Θ2H |
, |
Θ =1,1 1,87432 + 0,37492 |
+ 0,7497 2 = 2,1026 В. |
|
6. При однократных измерениях и отсутствии сведений о случайных по- |
||
грешностях за погрешность результата измерения |
принимают суммарную |
|
113 |
|
|

систематическую погрешность использованного средства измерения Θ . После округления получаем
=Θ = ±2,1 В.
Сучетом погрешности результат измерения запишется в виде
U ′ = (218,6 ± 2,1) В, Р = 0,95.
Задача 7.2
Исходное условие задачи 7.2 полностью совпадает с условием задачи 7.1. Дополнительно вводятся сведения о случайной погрешности. Предполагается,
что с доверительной вероятностью |
P = 0,95 случайная |
погрешность |
||
ε = 3,4248 В. |
|
|
|
|
Решение задачи |
|
|
|
|
Абсолютная суммарная погрешность результата измерения |
в этом слу- |
|||
чае оценивается соотношением |
K ( |
|
) , |
|
|
|
|
||
= ± |
Θ + ε |
|
|
|
где K ≈ 0,76 для доверительной вероятности P = 0,95 ;
Θ– суммарная систематическая погрешность (см. задачу 7.1).
ε– случайная погрешность
=±0,76(2,1026 + 3,4248) = ±4,2008 В.
После округления получаем |
= ±4 В. |
С учетом погрешности |
результат измерения запишется в виде |
U ′ = (219 ± 4) В, P = 0,95 . |
|
Задача 7.3
Исходное условие задачи 7.3 в основном совпадает с условием задачи 7.1. Дополнительно вводятся сведения о среднем квадратическом отклонении (СКО) средства измерения σ1 = 0,3782 В и СКО оператора σ2 = 0,4202 В.
114

Значения σ1 и σ2 найдены для n1 =10 и n2 = 20 , где n1 и n2 – числа изме-
рений при экспериментальной оценке рассматриваемых величин ( n1 при оценке
σ1 и n2 при оценке σ2). Решение задачи
Абсолютная неисключенная систематическая погрешность Θ , найденная в задаче 7.1, остается в силе и для данной задачи ( Θ = 2,1026 В).
При отсутствии корреляционной связи между величинами σ1 и σ2, суммарное среднее квадратическое отклонение σ:
σ = σ2 |
+σ2 |
= 0,37822 +0, 42022 = 0,5653 В |
1 |
2 |
|
σ = 0,5653 В.
Абсолютная случайная погрешность результата измерений ε запишется в
виде
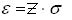 ,
,
где 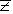 – коэффициент (
– коэффициент (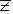 =2,0 для P = 0,95).
=2,0 для P = 0,95).
ε = 2, 0 0,5653 =1,130 В,
ε =1,130 В.
Абсолютная суммарная погрешность результата измерений :
= ±К( Θ + ε ) ,
где К = 0,76 для P = 0,95 ;
Θ– неисключенная систематическая погрешность;
ε– случайная погрешность.
Выражение для оценки « » правомерно, если справедливо соотношение
0,8 ≤ Θσ ≤ 8 .
Θ
Отношение σ имеет значение
Θσ = 0,2,10265653 = 3, 7194
115
т. е. приведенное выражение для оценки « » правомерно.
=±0,76(2,1026 +1,130) = ±2,4572 В,
=±2,4572 В.
После округления = ±2,5 В.
С учетом погрешности результат измерения запишется в виде
U′ = (218,6 ± 2,5) В,
Р= 0,95.
7.3.Погрешности косвенных измерений
Косвенное измерение − это измерение, при котором искомое значение величины находится по известной зависимости между этой величиной и величи-
нами , подвергаемыми прямым измерениям. Напомним, что прямое измерение − это измерение, при котором искомая величина определяется непосредственно из эксперимента по показаниям средства измерений.
7.3.1. Порядок оценки погрешностей классическим методом
Ниже излагается порядок оценки погрешностей косвенных измерений классическим методом для одного и для нескольких аргументов, по которым определяется результат косвенного измерения.
Рассмотрим зависимость
y = f(x),
где у – результат косвенного измерения (функция); х – результат прямого измерения (аргумент).
Предполагается, что погрешность измерения аргумента х известна и со-
ставляет величину ± x.
Погрешность измерения функции у обозначим через ± у и найдем ее зна-
чение по известным значениям величин у, х и ± x.
С учетом погрешностей ± x и ± y выражение (7.15) принимает вид
у ± y = f(х± x).
116

Разложим правую часть равенства (7.16) в ряд Тейлора и, пренебрегая
членами разложения, содержащими |
x в степени выше первой, получим |
||
y ± y = |
f (x) + x |
df (x) |
. |
|
|||
|
|
dx |
|
Учитывая соотношение (7.15), получим для величин у выражение y = ± x dfdx(x),
где y – абсолютная погрешность результата косвенного измерения величины у; x – абсолютная погрешность результата прямого измерения величины х.
Отметим, что выражение (7.18) является линейным приближением и в силу этого дает оценочные, приближенные значения погрешностей косвенных измерений. Допустимость использования соотношения (7.18) нормируется методическими указаниями МИ 2083–90 [48].
Относительная погрешность косвенного измерения δу определяется выражением
δy = ± yy = ± yx dfdx(x) ,
или
δy = ± yy 100% = ± yx dfdx(x) 100% ,
т. е. относительная погрешность может выражаться относительными величинами (см. (7.19)) или величинами в процентах (см. (7.20)).
Рассмотрим результат косвенных измерений для случая с несколькими аргументами, т. е.
у = f(x, z, ..., t),
где x, z, ..., t – результаты прямых измерений (аргументы); у – результат косвенного измерения (функция).
Значение суммарной абсолютной погрешности косвенного измерения у в этом случае находится по формуле
117

y = ± |
|
∂f 2 |
2 |
∂f 2 |
2 |
|
∂f 2 |
2 |
|
x + |
z + L+ |
t . |
|||||
|
|
∂x |
|
∂z |
|
|
∂t |
|
Значение суммарной относительной погрешности косвенного измерения
δу для рассматриваемого случая находится по формуле
δ |
|
= ± |
|
∂f |
2 |
|
|
2 |
|
∂f |
2 |
|
|
2 |
|
∂f |
2 |
|
2 |
y |
|
|
|
x |
+ |
|
|
|
z |
+ L + |
|
|
|
t |
|||||
|
|
|
y |
|
|
|
y |
|
|
|
y |
. |
|||||||
|
|
|
|
∂x |
|
|
|
|
∂z |
|
|
|
|
∂t |
|
|
|||
В (7.22) и (7.23) значения x, z, … , t – суммарные абсолютные погрешности результатов прямых измерений величин х, z, ... ,t. Соотношения (7.22) и (7.23) правомерны при условии, что рассматриваемые погрешности независимы (отсутствует связь между ними) и являются случайными величинами.
Соотношение (7.22) рекомендуется использовать для оценки погрешностей результатов косвенных измерений при определении искомой величины путем алгебраического суммирования аргументов (например, для функций вида y = x+z+t).
Ниже приведен пример оценки искомой величины и погрешности ее косвенного измерения по соотношению (7.22).
Соотношение (7.23) рекомендуется использовать для оценки погрешностей результатов косвенных измерений при определении искомой величины путем умножения, деления или возведения в степень аргументов,
подвергаемых прямым измерениям (например, для функций вида y = x tz 2 ).
Ниже приведен пример оценки искомой величины и погрешности ее косвенного измерения по соотношению (7.23).
Формулы для вычисления суммарных абсолютных и относительных погрешностей результатов косвенных измерений приведены в табл. 7.1.
В таблице приняты те же обозначения, что уже использовались выше,
т. е. x, z – абсолютные суммарные погрешности результатов прямых измере-
ний величин х и z; δx, δz – относительные суммарные погрешности результатов
118
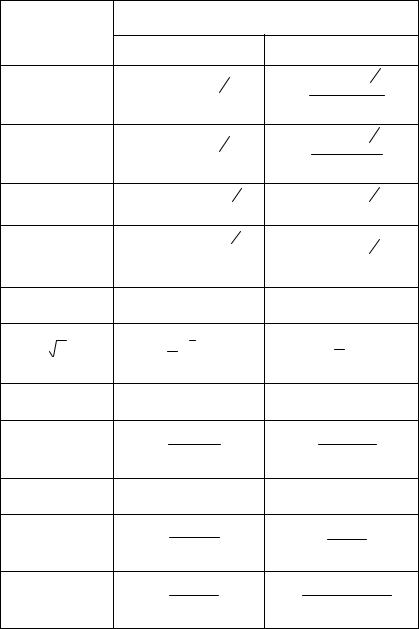
прямых измерений величин x И z; |
|
у и δу – абсолютные и относительные сум- |
||||||||
марные погрешности результата косвенного измерения величины у. |
||||||||||
|
|
|
|
|
|
|
|
|
Таблица 7.1 |
|
|
Погрешности косвенных измерений |
|||||||||
Функция (y) |
|
|
|
Погрешности |
|
|||||
абсолютная ( y) |
относительная (δy) |
|||||||||
|
||||||||||
x + z |
±[ 2x + 2z ]12 |
± [ 2х + 2z ]12 |
||||||||
|
|
|
|
|
|
|
|
|
x + z |
|
x- z |
|
2 |
|
2 12 |
|
|
[ 2х + 2z ]12 |
|||
±[ |
x |
+ |
z ] |
|
± |
|
|
x − z |
||
|
|
|
|
|||||||
x z |
± [x2 2z + z 2 2x ]12 |
|
±[δx2 +δz2 ]12 |
|||||||
x/z |
± [x2 2z + z 2 2x ]12 |
|
±[δx2 +δz2 ]12 |
|||||||
|
|
|
z 2 |
|
|
|
|
|
|
|
xn |
±nxn-1 x |
|
|
|
±nδx |
|||||
n x |
± |
1 x 1n −1 |
x |
|
|
|
± |
1 δx |
||
|
|
n |
|
|
|
|
|
|
n |
|
sinx |
± |
xcosx |
|
|
± |
x ctgx |
||||
tgx |
± |
|
x |
|
|
± |
2 x |
|||
(cos x)2 |
|
(sin 2x)2 |
||||||||
|
|
|
|
|
||||||
cosx |
± |
x sinx |
|
|
|
± |
x tgx |
|||
|
|
|
x |
|
|
|
|
2 x |
||
ctgx |
± (sin x)2 |
|
|
|
± sin 2x |
|||||
arctg x |
± |
|
x |
|
± |
|
|
|
x |
|
(1+ x2 ) |
(1 |
+ x2 )arctgx |
||||||||
|
|
|
||||||||
Изложенный порядок оценки значений погрешностей результатов кос- |
||||||||||
венных измерений может быть использован при известных значениях суммар- |
||||||||||
ных погрешностей результатов прямых измерений, по которым вычисляются |
||||||||||
результаты косвенных измерений. В случае же, когда известны составляющие |
||||||||||
(систематические и случайные) погрешностей результатов прямых измерений, |
||||||||||
119
необходимо воспользоваться рекомендациями, изложенными ниже в п. 7.3.2 учебного пособия.
7.3.2. Порядок оценки погрешностей по МИ 2083–90
Сформулируем основные положения, используемые при оценке погрешностей косвенных измерений по МИ 2083–90 [48].
Искомое значение величины А находится на основании результатов прямых измерений аргументов b, c, ..., s, связанных с искомой величиной уравнением
A = F (b, c, ..., s). |
(7.24) |
Для оценивания косвенно измеряемой величины и погрешностей результата измерения принято одно из допущений:
1)зависимость (7.24) линейная и отсутствует корреляция между погрешностями измерений аргументов;
2)зависимость (7.24) нелинейная, отсутствует корреляция между погрешностями измерений аргументов и допустим метод линеаризации рассматриваемой зависимости.
Случай для коррелированных погрешностей измерений аргументов и при недопустимости использования метода линеаризации зависимости (7.24) в данном учебном пособии не рассматривается. При необходимости этот материал может быть изучен самостоятельно (см. [21, 48]).
Предположим, что проведено n прямых измерений аргументов b, с, ..., s. Первому измерению соответствует значение, равное A1, второму измерению – A2 и т. д. Среднее арифметическое значение A и среднее квадратичеcкое откло-
нение σ результатов косвенных измерений вычисляются по формулам
|
|
|
|
1 |
n |
|
||
|
|
= |
∑Ai , |
|
||||
A |
|
|||||||
|
|
|
||||||
|
|
|
|
n i =1 |
|
|||
|
|
|
∑n (Ai − |
|
)2 |
|
||
|
|
A |
|
|||||
σ = |
i=1 |
|
|
|
|
, |
||
|
|
n −1 |
||||||
|
|
|
|
|
|
|||
где n – число измерений;
Ai – i-е значение результата косвенного измерения.
120
