1.6. Классическое определение вероятности

Существует класс опытов, в которых вероятность события можно вычислить, исходя из условий только самого этого опыта.

Пусть проводится эксперимент (опыт), который имеет nразличныхэлементарных исходов, то есть при каждом испытании обязательно один из этих возможных исходов реализуется. Совокупность всех возможных исходов испытания называетсяпространством элементарных исходов. Те элементарные исходы, в которых интересующее нас событие наступает, называютсяблагоприятствующими исходамиэтому событию.

Например, при подбрасывании игральной кости (кубика) один раз имеем шесть исключающих друг друга исходов: выпадение 1, 2, 3, 4, 5, 6 очков. Это и есть пространство элементарных исходов. Событие А –“выпадение четной цифры” имеет три благоприятствующих исхода: 2, 4, 6 очков.

Классическим определением вероятности можно воспользоваться, если число возможных исходов испытания конечно, все элементарные исходы равновозможны, несовместны и образуют полную группу.

Определение. Вероятностью события Аназывается отношение числа исходов, благоприятствующих событиюА, к общему числу всех возможных исходов:

,

где m– число исходов, благоприятствующих событиюА, n– число всех возможных исходов испытания.

В приведенном примере с подбрасыванием игральной кости Р(А) = 3/6 == 1/2.

Классическое определение вероятности служит хорошей математической моделью тех случайных явлений, для которых важнейшим условием применения является предположение о равновозможности исходов опыта. Такие требования естественны в области азартных игр, лотерей, в организации выборочного контроля и выборочных статистических исследований. Исторически первые применения вероятностных методов относятся к XVII веку, когда разрабатывалась теория азартных игр с целью дать рекомендации игрокам. Затем эти методы стали применяться в практике страховых компаний для установления разумных страховых премий. В настоящее время практически нет области знаний, где не могли бы применяться эти методы исследования.

Подсчет числа исходов в классических случаях часто сводится к задачам комбинаторики (подразд. 1.1).

1.7. Свойства вероятностей

Из определения вероятности вытекают следующие ее свойства.

1. Вероятность любого события есть число, заключенное между нулем и единицей:

0Р(а)1.

Действительно, если событию Аблагоприятствуетmисходов из возможныхn исходов, то0mn, откуда 0.

Вероятность достоверного события А равна единице, так как все исходы благоприятствуют событию (m=n) и Р(А) = n/n=1. Вероятность невозможного события А равна нулю, так как этому событию не благоприятствует ни один исход и Р(А) = 0/n =0 . Вероятность любого случайного события А есть положительное число, заключенное между нулем и единицей: 0 < Р(А) < 1.

2. Если АиВнесовместные события, то

Р(А+В) = Р(А) + Р(В).

Пусть эксперимент имеет nравновозможных исходов, из которых исходов благоприятствуют событиюА, а исходов – событиюВ. Так как событияАиВнесовместимы, то среди исходов нет благоприятствующих и тому и другому одновременно. Поэтому событиюА + Вблагоприятствуетm₁+ m₂ исходов. Следовательно,

Р(А+ В) = Р(А) + Р(В).

3. Вероятность события , противоположного событиюА, равна:

Р() = 1 –Р (А).

В самом деле, при каждом осуществлении комплекса условий обязательно произойдет одно из событий Аили, т.е.А + =(достоверное).

Cледовательно,Р (А +)= 1, а так как событияАинесовместны, то по свойству 2 имеемР (А) + Р ()= 1.

Рассмотрим несколько примеров.

Пример 1.5.

В семь дней недели независимо друг от друга происходит семь событий (скажем, автомобильные аварии). Какова вероятность, что каждый день будет происходить по одному событию?

Решение

Для удобства рассуждений описанную ситуацию формализуем и представим следующим образом. Имеем семь ящиков и семь различных шаров. Тогда распределение событий по дням недели равносильно раскладке шаров по ящикам. (Подобная модель с шарами часто используется в задачах). Первый шар можно положить в любой из семи ящиков, второй – также в любой из семи и т.д., поэтому всех возможных способов раскладки шаров по ящикам будет 7⁷. Для получения числа благоприятствующих исходов разложим по одному шару в каждый ящик, а затем будем менять местами шары. Тогда число благоприятствующих случаев будет равно числу перестановок, т.е. 7!. Все элементарные исходы опыта равновозможны и, следовательно, можно воспользоваться классической формулой. В итоге имеем

Р=0,0062.

Оказалось, что маловероятно равномерное распределение событий во времени, что согласуется с обыденным представлением о «полосе везения» и «полосе невезения» и т. п. ситуациях.

Пример 1.6.

Из MдеталейNбракованных. Наугад выбираетсяnдеталей. Какова вероятность, что среди выбранных будетmбракованных?

Решение

Так как нас интересует только состав выбора (порядок неважен), то возможных способов выбора будет . Интересующее нас событие произойдет, еслиmдеталей будет выбрано из числаМбракованных, это можно сделатьспособами, и для каждого набора изmбракованных деталей будет выбраноn-mгодных деталей изN-M, что можно сделатьспособами. Согласно комбинаторному принципу всего способов, благоприятствующих событию, будет. Искомая вероятность равна их отношению

.

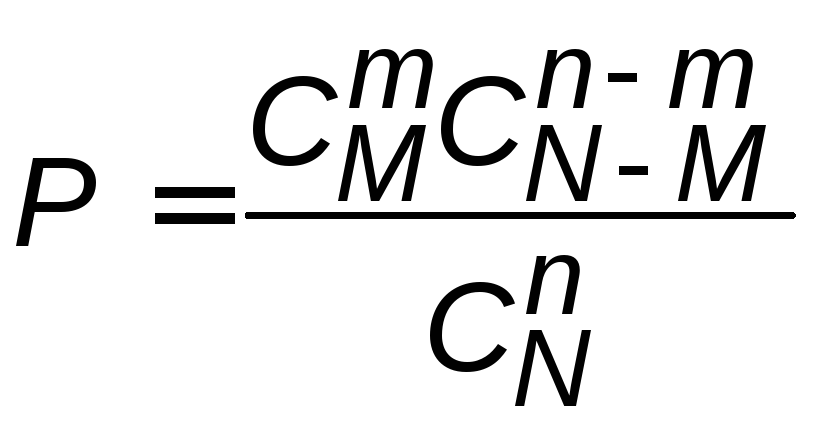Пример 1.7.

Из Nбилетов студент не выучилMбилетов. Когда больше вероятность выбрать невыученный билет: когда тянешь билет первым или последним?

Решение

Рассмотрим событие «студент выбирает билет r-м по счету». При подсчете общего числа возможных способов выбора первыхrбилетов важно, какие билеты были выбраны (важен состав) и в каком порядке они выбраны, т.е. число размещений изNпоr: . «Благоприятствуют» выбору невыученного билета те способы, в которыхr-й билет выбран из числа невыученныхМбилетов и для каждого из этихМбилетов предыдущие с учетом состава и порядка могут быть выбраныспособами. Согласно комбинаторному принципу, всего благоприятствующих способов будетM. Тогда вероятность вытянуть невыученный билет равна:

.

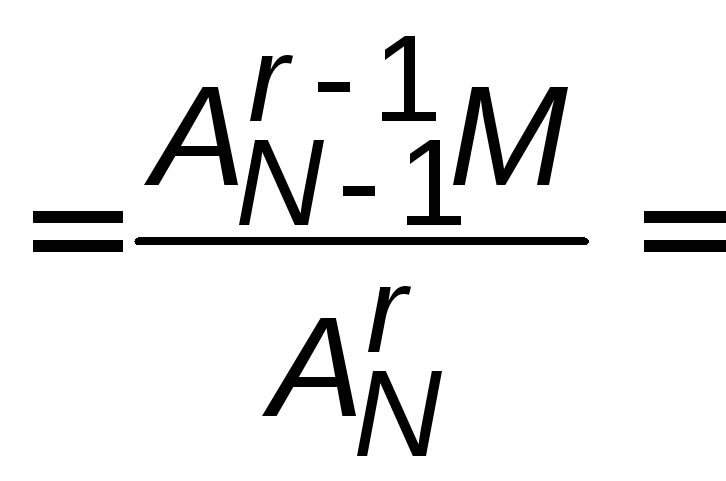
Результат малоутешительный для нерадивых студентов так как не зависит от того, когда студент тянет билет: первым или последним.