3.3.2. Показательный закон распределения
Показательный закон
распределения определяется интегральной
функцией распределения: 
,
где>0 –некоторый
параметр. График этой функции изображен
на рис. 3.3.
Рис. 3.3
Из графика видно, что P(X<0)=F(0)=0, т.е. X принимает только неотрицательные значения. Кроме того, значения, близкие к нулю, более вероятны, нежели все другие. Функция возрастает вблизи нуля наиболее быстро, и ее приращения, равные вероятности попадания в интервал, для интервалов, расположенных вблизи нуля, будут больше, чем для таких же интервалов, расположенных в любом другом месте числовой оси. По такому закону распределено, например, время безотказной работы бытовых приборов и других сложных устройств.
Следует отметить, что показательный закон распределения тесно связан с рассмотренным выше распределением Пуассона.
Пусть случайные события на
оси времени распределены по закону
Пуассона с параметром
,
т.е. вероятность того, что на отрезке
времени длительностих
произойдет m
событий, равна: P(m)=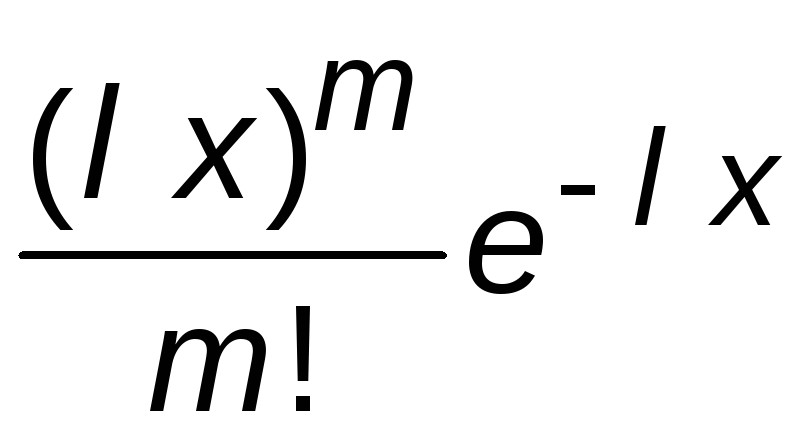
.
Зафиксируем момент наступления события
и найдем вероятность того, что до момента
наступления следующего события пройдет
времени больше, чем х.
Это означает, что за время х
не появится ни одного события и Р(0)=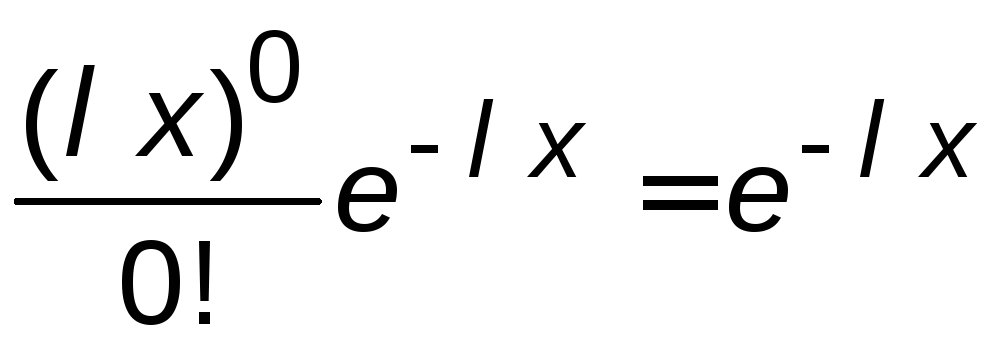
. Тогда вероятность того, что между
моментами появления событий времени
будет меньше х,
равна 1-е
(как
вероятность противоположного события).
В результате приходим к показательному
распределению
P(X<x)=F(х)=
1-e
.
Поток, в котором интервалы между моментами наступления последовательных событий распределены по показательному закону, называется простейшим или Пуассоновским. Итак, если события во времени или пространстве распределены по закону Пуассона, то интервалы между последовательными событиями распределены по показательному закону.
Замечание. Пусть дискретная случайная величина имеет закон распределения:
|
X |
|
|
|
… |
|
|
|
P |
|
|
|
… |
|
. |
Тогда её интегральная функция распределения имеет вид ступенчатой функции (рис. 3.4).
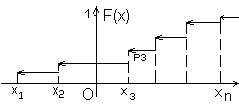
Рис. 3.4
Скачки функции равны вероятностям соответствующих значений X.
Интегральная функция непрерывной случайной величины представляет собой непрерывную функцию. Можно привести примеры таких случайных величин, интегральная функция которых не везде является непрерывной неубывающей функцией, а в некоторых точках имеет разрывы. Такие величины называют смешанными случайными величинами.
3.3.3. Дифференциальная функция распределения
Дифференциальной функцией распределения, или функцией плотности вероятности называется первая производная от интегральной функции распределения, т.е. F'(х)=f(х). Из этого определения видно, что функция плотности вероятности существует только для непрерывных случайных величин.
Пусть случайная величина X задана функцией плотности вероятности f(х). Вероятность того, что эта случайная величина примет значения, принадлежащие интервалу [a,b], равна определенному интегралу от дифференциальной функции распределения в пределах от a до b:
.
Это следует из того, что P(a<X<b)=F(b)-F(a), а по формуле Ньютона-Лейбница
.
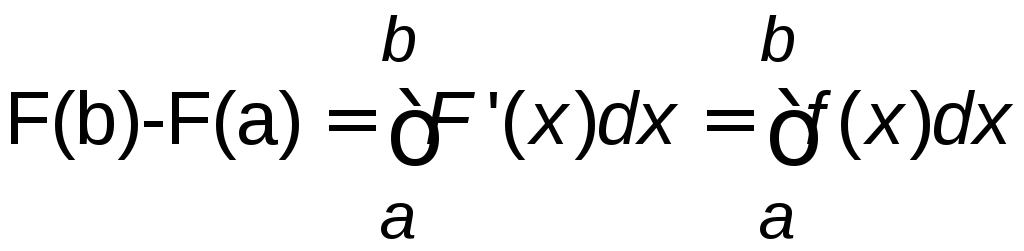Геометрически полученный результат можно истолковать так: вероятность того, что случайная величина X примет значение, принадлежащее интервалу [a,b], равна площади, которая опирается на этот интервал и ограничена сверху кривой f(х).
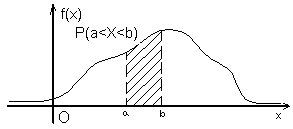
Рис. 3.5
Свойства дифференциальной функции распределения:
1.
,
так какf(х)
является производной от неубывающей
функции F(x).
2.
,
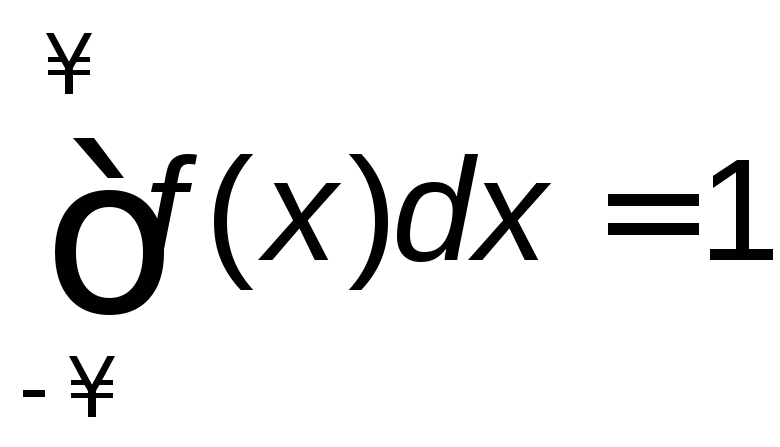т.е. площадь, заключенная между осьюОх
и функцией f(x),
равна единице. Это следует из того, что
,
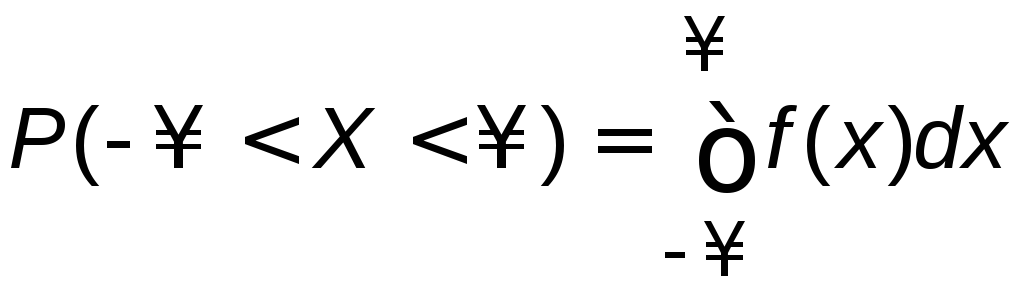а событие
является достоверным, и его вероятность
равна единице.