3.3.4. Равномерное распределение

Равномерный закон распределения имеет функцию плотности вероятности вида:

П

Рис. 3.6

ри этом законе распределения плотность вероятности на интервале [a,b] постоянна и равновозможны любые значения из этого интервала (рис. 3.6).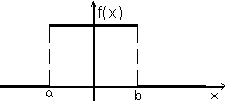

В качестве примера равномерно распределенной случайной величины можно назвать ошибку округления, скажем, до 0,01, то это означает, что ошибка округления равномерно распределена в интервале [-0,005; 0,005].

3.3.5. Распределение Коши

Закон распределения Коши задается функцией плотности вероятности: (Коши в свое время заблуждался, считая, что ошибки измерения распределены по этому закону). График этой функции изображен на рис. 3.7.

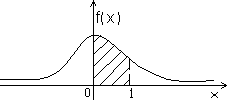
Рис. 3.7

Вычислим, например, вероятность того, что случайная величина, распределенная по закону Коши, примет значение из интервала [0,1]:

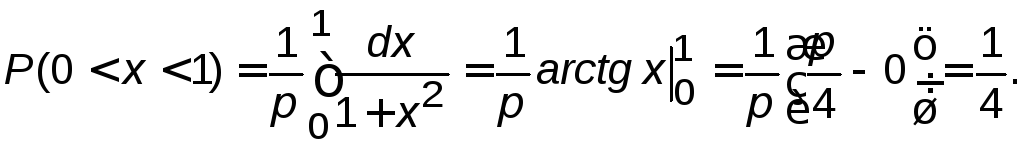
Замечание. По функции плотности вероятности можно легко найти интегральную функцию распределения.

Так как F(x)=P(X<x) и ,

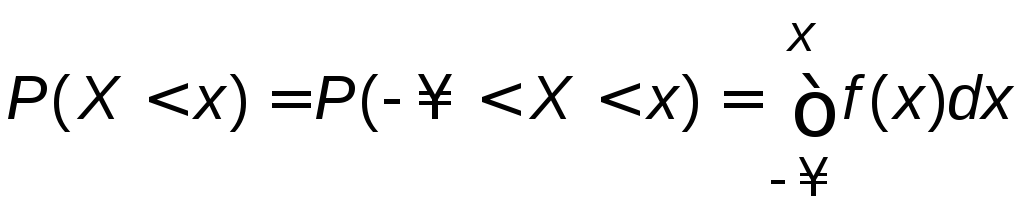то .

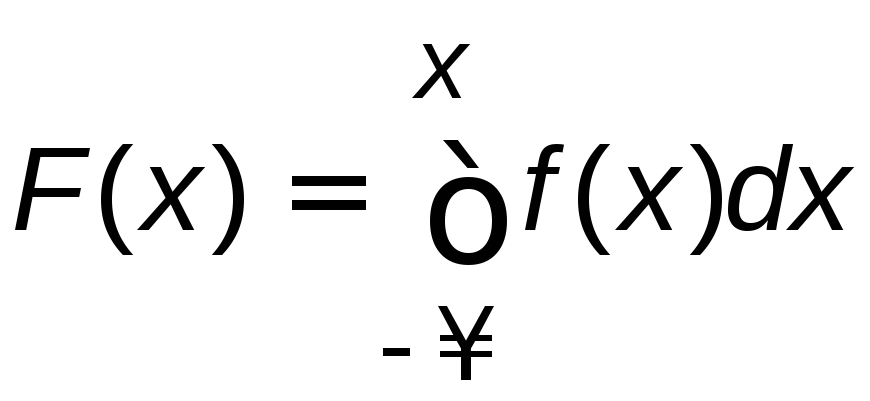4. Числовые характеристики случайных величин

Закон распределения случайной величины дает исчерпывающую информацию о случайной величине. Однако иногда можно охарактеризо­вать достаточно ярко случайную величину с помощью всего одного или нескольких чисел. Например, можно указать закон распределения количества осадков, выпадающих в данной местности за определенный месяц, но проще и нагляднее указать среднее количество осадков в данном месяце.

Числа, назначение которых в сжатом виде характеризовать основные особенности распределений случайных величин, называются числовыми характеристиками. Рассмотрим некоторые из числовых характеристик и их основные свойства.

4.1. Математическое ожидание и его свойства

4.1.1. Математическое ожидание

Математическим ожиданием(или средним значением)дискретнойслучайной величины называется сумма произведений всех её возможных значений на соответствующие им вероятности. Т.е., если случайная величина имеет закон распределения

X			…		,
P			…

то математическое ожиданиевычисляется по формуле

.

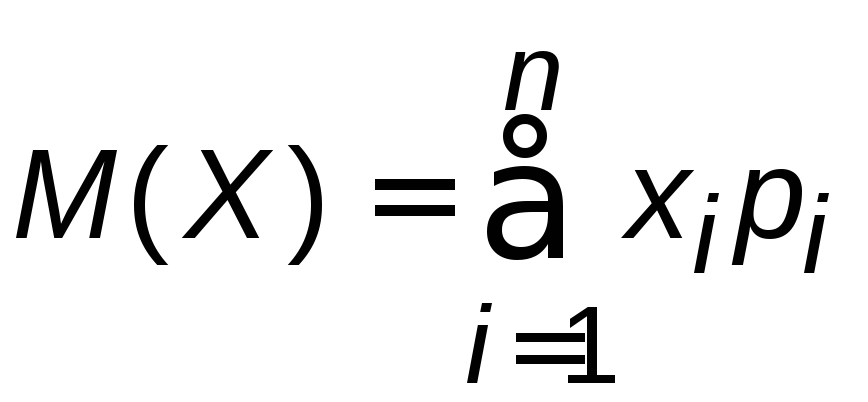Если случайная величина имеет бесконечное число значений, то математическое ожидание определяется суммой бесконечного ряда: , при условии, что этот ряд абсолютно сходится (в противном случае говорят, что математическое ожидание не существует).

Для непрерывной случайной величины, заданной функцией плотности вероят­ности f(x), математическое ожидание определяется в виде интеграла

,

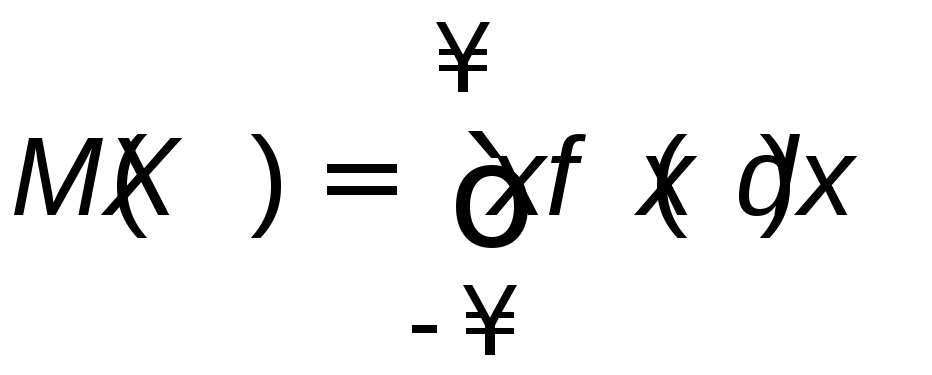при условии, что этот интеграл существует и абсолютно сходится (если интеграл расходится, то говорят, что математическое ожидание не существует).

Пример 4.1.

Определим математическое ожидание случайной величины, распределённой по закону Пуассона. По определению

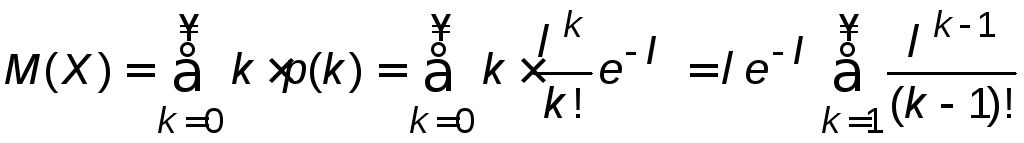
или обозначим . Тогда

.

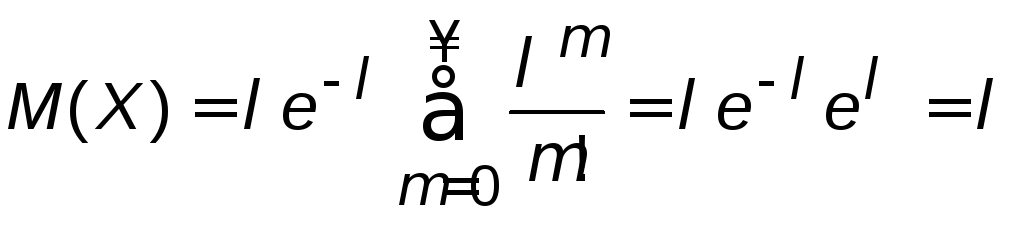Значит, параметр , определяющий закон распределения пуассоновской случайной величины, равен среднему значению этой величины.

Пример 4.2.

Для случайной величины, имеющей показательный закон распределения (), математическое ожидание равно:

.

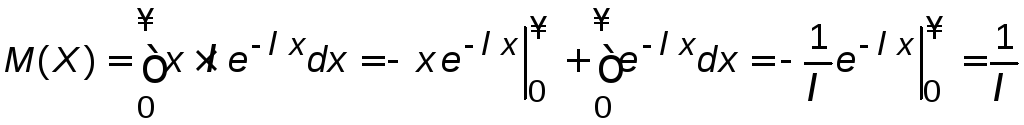В данном интеграле пределы взяты с учётом того, что f(х) отлична от нуля только при положительных x.

Пример 4.3. Случайная величина, распределенная по закону распределения Коши, не имеет среднего значения. Действительно

.

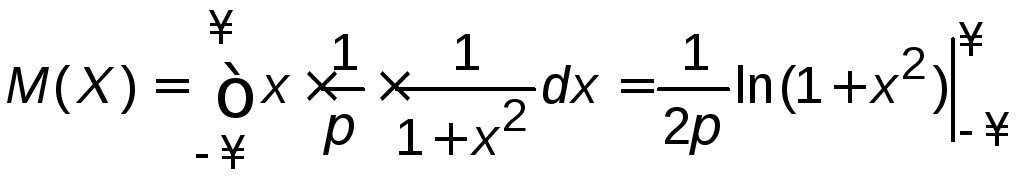Данный интеграл не существует (проверьте самостоятельно).