6.9. Двумерный нормальный закон распределения

Систему случайных величин можно интерпретировать как случайную точку на плоскости. Нормальный закон распределения для системы (Х,У) называется двумерным нормальным законом распределения и имеет плотность вероятности

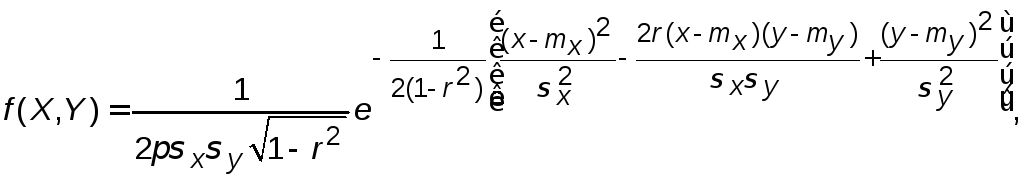
где – математические ожидания соответственно случайных величинХ и У, – средние квадратические отклонения этих величин,r – коэффициент корреляции Х и У. Поверхность f(x,y) имеет вид холма, вершина которого находится над точкой (m_x, m_y) (рис. 6.1).

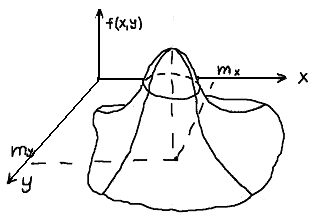
Рис. 6.1

Двумерный нормальный закон распределения имеет, например, точка попадания снаряда из орудия, которое хорошо пристреляно по цели имеющей координаты ().

Если случайные величины независимы, то r=0 и функция плотности вероятности f(x,y) имеет вид

Рис. 6.2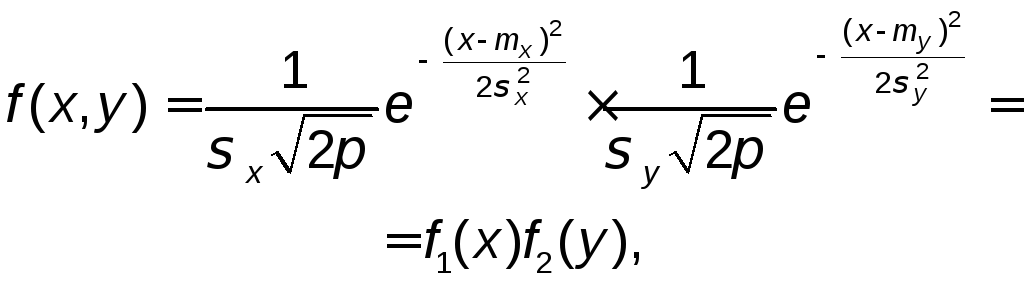

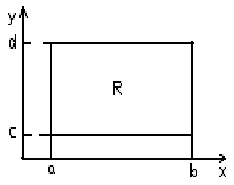
что соответствует свойству систем независимых случайных величин.

Используя формулу (5.2) и f(x,y), можно вычислить вероятность попадания ХУ в любую область плоскости. Особенно просто это сделать, если Х и У независимы, а область представляет собой прямоугольник со сторонами, параллельными осям координат (рис. 6.2).

.

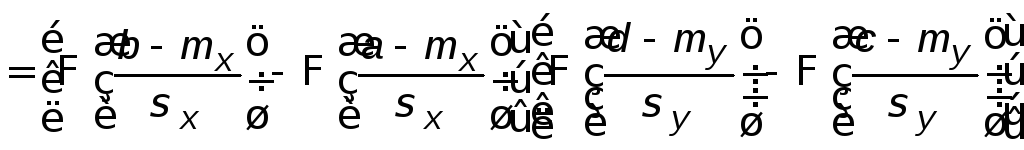Можно ввести в рассмотрение нормальные законы распределения, имеющие большую размерность, например трёхмерные.

7. Предельные теоремы теории вероятностей

В конце XIX века в теории вероятностей возникло направле­ние исследований, которое получило название: предельные теоремы теории вероятностей. В этом направлении, начало которого было положено нашими соотечественниками П.Л. Чебышевым, А.А. Марковым, А.М. Ляпуновым, по сей день ведутся интенсивные исследования. Предельные теоремы теории вероятностей можно разбить на две боль­шие группы.

1. Одна группа теорем составляет "закон больших чисел". Закон больших чисел формулирует условия, при которых совокупное действие большого числа случайных факторов приводит к результату почти не зависящему от случая (т.е. практически постоянный результат).

2. Вторая группа теорем связана с выяснением вопроса о распределении сумм большого числа случайных величин. В этих теоремах выясняется, какие законы распределения может иметь сумма случайных величин, если число слагаемых неограниченно увеличивается, и какие условия при этом нужно наложить на сами величины. В частности, центральная предельная теорема посвящена установлению условий, при которых возникает нормальный закон распределения сумм.

7.1. Центральная предельная теорема

Первый вариант этой теоремы был доказан в 1912 г. А.М. Ляпуновым. В настоящее время имеется несколько формулировок этой теоремы, различающихся условиями, которые накладываются на случайные величины. Мы приведём простейший вариант центральной предельной теоремы для одинаково распределённых независимых случайных величин.

Пусть последовательность одинаково распределённых случайных величин с математическими ожиданиямии дисперсиями.

Теорема. Если случайные величины независимы и, то при достаточно большомn закон распределения суммы 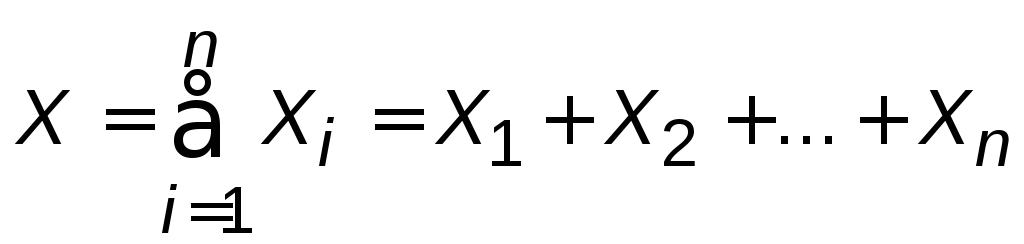будет сколь угодно близок к нормальному закону распределения .

Так как в условиях теоремы случайные величины независимы, то

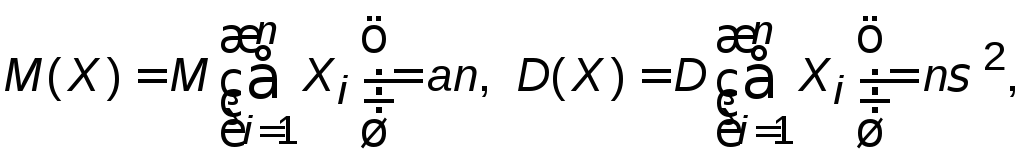т.е. в условиях теоремы сумма имеет закон распределения, близкий к .Так какna и с ростом n, возрастают, то удобнее рассматривать не просто суммы , а нормированные суммы: 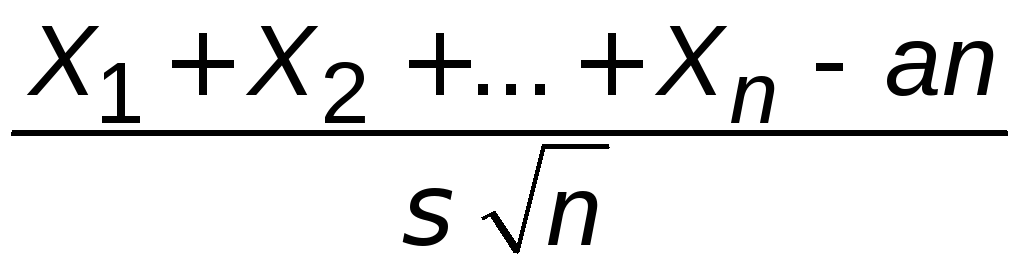. Такие суммы при n→имеют закон распределения.

Мы не приводим доказательства теоремы потому, что оно требует введения многих дополнительных понятий и утверждений. Было потрачено немало усилий, чтобы ослабить условия, налагаемые на случайные величины в центральной предельной теореме. В частности, оказалось, что утверждение теоремы остаётся в силе и для слабо зависимых случайных величин. Как уже отмечалось, существует много вариантов и соответственно формулировок центральной предельной теоремы, но во всех этих вариантах суть условий одна: если случайная величина может быть представлена в виде суммы большого числа независимых (или слабо зависимых) случайных величин, каждая из которых мала по сравнению с суммой, то эта сумма имеет закон распределения, близкий к нормальному.

Пример 7.1.

Наглядной иллюстрацией действия центральной предельной теоремы является рассеивание снарядов при артиллерийской стрельбе. На траекторию снаряда действует большое количество независимых факторов, влияние каждого из которых невелико. Этими факторами являются отклонения в размере заряда, в размере и весе снаряда, сила и направле­ние ветра на разных высотах, плотность воздушных вихрей, зависящая от температуры и влажности воздуха, и т.д.

В результате отклонение снаряда от цели имеет приблизительно нормальный закон распределения.

Пример 7.2.

Другими широко известным примером может служить ошибка, возникшая при измерениях. Ошибка, как правило, является суммой малых ошибок, возникающих из-за действия случайных факторов, таких, как температура окружающей среды, состояние наблюдателя, состояние измерительного прибора и т.д., поэтому в теории ошибок в качестве математической модели часто используется нормальный закон распределения.