6.4. Зависимые и независимые случайные величины

В предыдущем пункте было показано на примере дискретных случайных величин, как, зная закон распределения системы (Х,Y) ,найти законы для отдельных величинХиY. Естественно, возникает вопрос – можно ли, зная законы для отдельныхХиY, входящих в систему, получить закон для системы.

Оказывается, в общем случае этого сделать нельзя: знание законов распределения для ХиYне дает возможности найти закон распределения системы. Это можно сделать только в одном частном случае: когдаХиY, образующие систему,независимы.

Случайные величины XиY, образующие систему, называютсянезависимыми, если закон распределения одной из них не зависит от того, какое значение приняла другая случайная величина. Иными словами, зная результат наблюдения над одной случайной величиной, ничего нельзя сказать дополнительно о другой случайной величине.

Системы независимых случайных величин обладают важным свойством: случайные величины XиYнезависимытогда и только тогда, когда интегральная (дифференциальная) функция распределения системы (X,Y) равна произведению интегральных (дифференциальных) функций распределения случайных величинХиY, составляющих систему, т.е.

и ,

где и  – интегральная и дифференциальная функции распределения случайной величиныХ, а и  – соответствующие функции случайной величиныY.

6.5. Операции над случайными величинами

Поставим такую задачу: зная законы распределения отдельных случайных величин ХиY, найти закон распределения системы (Х,Y) этих случайных величин. Примерами таких совокупностей случайных величин являютсяX+Y,X-Y,ХY,X,kX(k=const) и.т.д.

Как отмечено выше, это можно сделать, если случайные величины ХиY, образующие систему,независимы.

Рассмотрим XиY– две независимые дискретные случайные величины с законами распределения соответственно:

X

…

…

Y

…

…

.

P

…

…

P

…

…

Тогда система (X, Y) этих случайных величин принимает свои значения с вероятностями (с учетом независимостиXиY):

.

Таким образом, вероятность того, чтоХ примет значение , аY – значение , равна произведению соответствующих вероятностей:

Сумма случайных величинXиY– это новая случайная величинаX +Y, которая принимает все значения вида с вероятностями .

Аналогично определяются разность и произведение случайных величин.

Разность Х–Y(произведение XY) случайных величинXиY –- новая случайная величина, которая принимает все значения вида: и с такими же вероятностями , с какими случайная величинаX +Yпринимает соответствующие значения.

Произведение kXслучайной величиныХна постоянную величинуk – новая случайная величина, которая с теми же вероятностями, что иХ, принимает значения, равные произведениям значенийХна k.

Х±У	xi ± yj		XY	xi · yj
Р		,	P

Квадрат случайной величины Х, т.е. – новая случайная величина, которая принимает свои значения с теми же вероятностями, что и Х.

Заметим, что случайные величины Х+Х и 2Химеют разные законы. Это же относится к случайным величинам и .

Пример 6.4.

Два стрелка независимо друг от друга делают по два одиночных (независимых) выстрела каждый по своей мишени. Вероятность попадания при одном выстреле для первого стрелка равна 0,7; для второго – Случайная величинаX– число попаданий в мишень первого стрелка,Y –число попаданий второго стрелка.

Составить законы (ряды) распределения:

а) отдельных случайных величин ХиY;

б) случайных величин Х+YиXY,

в) найти соответствующие математические ожидания M(X+Y)иM(XY), дисперсииD(X+Y),D(XY), средние квадратические отклонения .

Решение

а) Возможные значения случайных величинХиY:

.

Соответствующие им вероятности вычисляем, пользуясь правилами сложения и умножения вероятностей.

Ряды распределения случайных величин ХиУимеют вид:

Х	0	1	2
P	0,3·0,3=0,09 не попал 2 раза	0,7·0,3+0,3·0,7=0,42 попал один раз из двух	0,7·0,7=0,49 попал оба раза

Контроль: ;М(Х)=.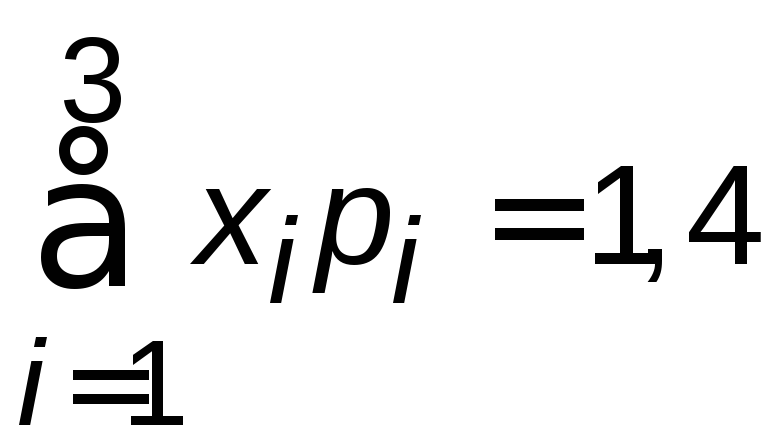

Y	0	1	2
P	0,6·0,6=0,36 не попал 2 раза	0,4·0,6+0,6·0,4=0,48 попал один раз из двух	0,4·0,4=0,16 попал оба раза

Контроль: .

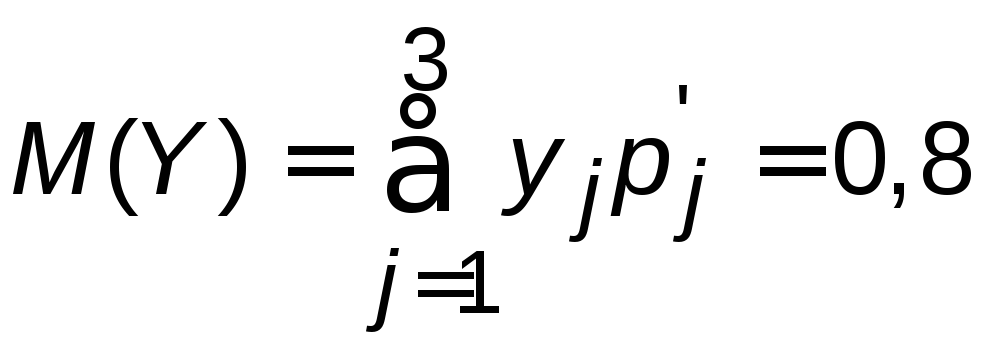Таким образом, получены законы распределения ХиY:

X	0	1	2		Y	0	1	2
P	0,09	0,42	0,49		P	0,36	0,48	0,16

б) Найдем все возможные значения случайных величинX+Yи и вероятности, с которыми они принимают их. Составим вспомогательную таблицу:

X	Y	X+Y	P	XY
0	0	0		0
0	1	1	0,09	0
0	2	2	0,09	0
1	0	1	0,42	0
1	1	2	0,42	1
1	2	3	0,42	2
2	0	2	0,49	0
2	1	3	0,49	2
2	2	4	0,49	4

Случайная величина Х+Yпримет, например, значение 0, еслиХпримет значение 0 иY –тоже значение 0. Вероятность такого случая в соответствии с теоремой умножения вероятностей равна произведению вероятностей (см. первую строку таблицы). Аналогично вычисляются вероятности других случаев.

Случайная величина Х+Yпринимает 5 различных значений:0; 1; 2; 3; 4. Значение1она принимает два раза – в случае, записанном во второй строке, или в случае, указанном в четвертой строке. Так как эти случаи – события несовместные, то по теореме сложения вероятность того, чтоХ+Yпримет значение1, равна

P(Х+Y =1)= 0,0432+0,1512=0,1944.

Точно так же подсчитываются вероятности для других повторяющихся значений Х+Y.

В итоге получим закон распределения X + Y(две верхние строки):

X+Y	0	1	2	3	4
P	0,0324	0,1944	0,3924	0,3024	0,0784
	0	1	4	9	16	.

Контроль: P= 0,0324 + 0,1944 + 0,3924 + 0,3024 + 0,0784 = 1.

Значения случайной величины находятся аналогично. Вероятности различных случаев вычисляются также с помощью теоремы умножения вероятностей. Случайная величинаX  Yможет принимать четыре различных значения:0; 1; 2; 4. Значение0она принимает в пяти несовместных случаях. Поэтому по теореме сложения вероятностей

P(X·Y = 0)= 0,0324 + 0,0432 + 0,0144 + 0,1512 + 0,1764 = 0,4176.

Следовательно, закон распределения X  Yимеет вид:

	0	1	2	4
P	0,4176	0,2016	0,3024	0,0784

Контроль: P= 0,4176 + 0,2016 + 0,3024 + 0,0784 = 1.

в) Математическое ожиданиеM(X + Y)можно вычислить двумя способами.

Во-первых, непосредственно, пользуясь полученным законом распределения X + Y:

M(X + Y)= .

Во-вторых, используя свойство: M(X + Y)=M(X)+M(Y)=1,4+0,8=2,2.

M(X) =1,4 и M(Y)=0,8 получены в пункте а). Результаты, естественно, совпали.

Аналогично: M(XY)==1,12.

Тот же результат получим, пользуясь свойством для независимых случайных величин

M(X Y) = M ( X )= 1,4.

Для независимых случайных величин ХиYдисперсию суммы можно найти, пользуясь свойством:D(X+Y)=D(X)+D(Y), гдеD(X)=M(X-(M(X))иD(Y) = M(Y- (M(Y)). Получим законы распределения для и , используя полученные (см. пример 6.4., пункта) законы дляXиY:

M(X)= 02,38;

.

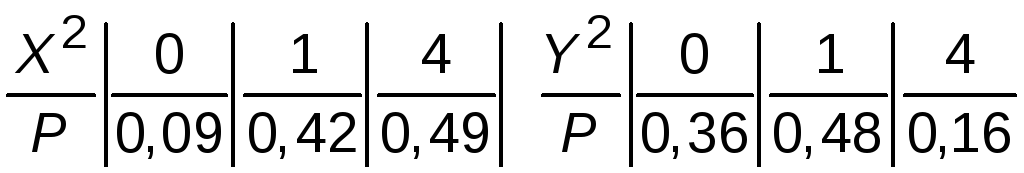D(X)= 2,38 – (1,4)²= 0,42;

= = 0,648.

Аналогично

M(Y)= 0,48+0,64 = 1,12;

D(Y)= 1,12 – (0,8)= 0,48; = = 0,693.

Теперь можно найти дисперсию суммы D(X+Y)=D(X)+D(Y)=0,42+0,48=0,9.

Такой же результат получим, пользуясь формулой:

D(X+Y) = M(X+Y)² – (M(X+Y))².

Закон для получен (см. пример 6.4., пунктб– две нижние строки).

M(X+Y)=0

D(X+Y)= 5,74 – (2,2)= 0,9,

= .

Для определения дисперсии D(X Y)найдемM(X Y), тогда по формуле

D(X Y) = M(X Y)- (M(X Y)).

.

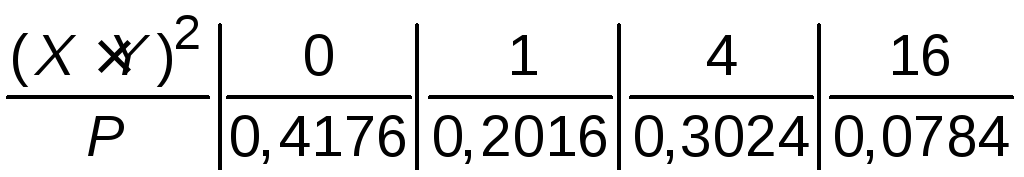M(X Y) = 0,2016 + 1,2096 + 1,2544 = 2,6656;

D(X Y)= 2,6656 – (1,12)= 2,6656 – 1,2544 = 1,4112;

= = 1,1879.