4.1.2. Свойства математического ожидания

Свойство 1. Математическое ожидание постоянной равно самой этой постоянной.

Постоянная С принимает это значение с вероятностью, равной единице, и по определению М(С)=С1=С.

Свойство 2. Математическое ожидание алгебраической суммы случайных величин равно алгебраической сумме их математических ожиданий.

Ограничимся доказательством этого свойства только для суммы двух дискретных случайных величин, т.е. докажем, что

Под суммойдвух дискретных случайных величин понимается случайная величина, которая принимает значенияс вероятностями.

По определению

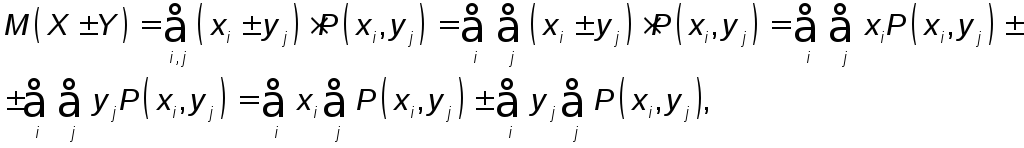
но ,

где – вероятность события, вычисленная при условии, что. В правой части последнего равенства перечислены все случаи появления события, поэтомуравна полной вероятности появления события, т.е.. Аналогично. Окончательно имеем

.

Свойство 3.Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

Приведем доказательства этого свойства только для дискретных величин. Для непрерывных случайных величин оно доказывается аналогично.

Пусть ХиУнезависимы и имеют законы распределения

Х			…		,
Р			…

У			…		.
Q			…

Произведением этих случайных величин будет случайная величина, которая принимает значения с вероятностями, равными (в силу независимости случайных величин). Тогда

Следствие. Постоянный множитель можно выносить за знак математического ожидания.

Так как постоянная С не зависит от того, какое значение примет случайная величина X, то по свойству 3. имеем

М(С·Х)=М(С)М(Х)=СМ(Х).

Если a и b постоянные, то М(а·Х+b)=а·М(Х)+b.

Пример 4.4.

Математическое ожидание числа появления события в схеме независимых испытаний.

Пусть производится n независимых опытов, вероятность появления события в каждом из которых равна р. Число появлений события в этих n опытах является случайной величиною Х, распределённой по биномиальному закону. Однако непосредственное вычисление её среднего значения громоздко. Для упрощения воспользуемся разложением, которым будем пользоваться в дальнейшем неоднократно. Число появлений события в n опытахсостоит из числа появлений события в отдельных опытах, т.е.

где имеет закон распределения, рассмотренный в примере 3.2 (принимает значение 1, если событие в данном опыте произошло, и значение 0, если событие в данном опыте не появилось).

	0	1	.
Р	1-р	р

Поэтому илит.е. среднее число появлений события вnнезависимых опытах равно произведению числа опытов на вероятность появления события в одном опыте.

Например, если вероятность попадания в цель при одном выстреле равна 0,1, то среднее число попадания в 20 выстрелах равно 200,1=2.

4.2. Дисперсия и среднее квадратическое отклонение

Дисперсия и среднее квадратическое отклонение дают представление о разбросе случайных величин относительно их среднего значения.