6.6. Числовые характеристики системы двух случайных величин

Числовые характеристики системы случайных величин (X,Y) состоят из числовых характеристик каждой из величин, входящих в систему, и числовых характеристик, дающих представление о характере связи между величинами. Числовые характеристики каждой из величин по отдельности определяются как числовые характеристики обычных случайных величинХиY. Из числовых характеристик зависимости между величинами назовем лишь наиболее употребляемые.

6.6.1. Ковариация двух случайных величин

Корреляционным моментомиликовариацией случайных величинХиYназывается математическое ожидание произведения соответствующих центрированных величин

cov(X,Y) == М((Х-М(Х)(Y-M(Y)).

Если случайные величины независимы, то их ковариация равна нулю. Обратное утверждение верно не всегда. Равенство нулю ковариации независимых случайных величин следует из теоремы о математическом ожидании произведения независимых случайных величин:

cov(X,Y)== 00 = 0.

Ковариация двух случайных величин характеризует не только степень зависимости случайных величин, но и их рассеивание вокруг точки (M(X); M(Y)).

Ковариацию часто удобно выражать через начальные моменты случайных величин:

Таким образом, ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение математических ожиданий.

6.6.2 Коэффициент корреляции

Размерность ковариации cov(X, Y) равна произведению размерностей случайных величинХиY. Безразмерной характеристикой зависимостиХиYявляетсякоэффициент корреляции

.

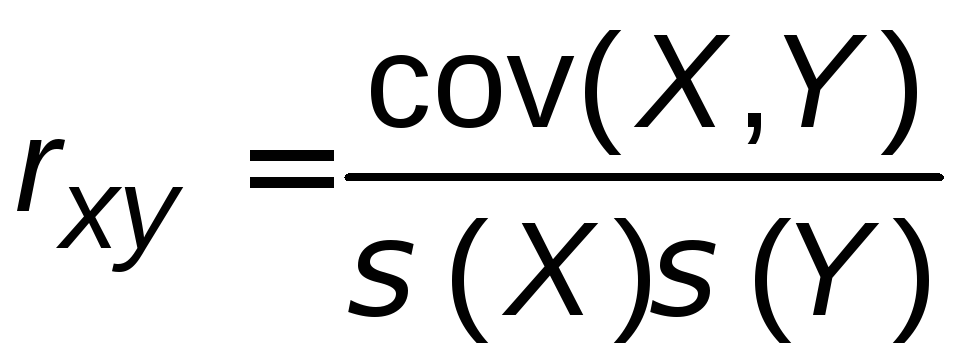Коэффициент корреляции случайных величин ХиYхарактеризует силу зависимости этих величин, причем тольколинейную зависимость. Если, то случайные величиныХиYсвязаны положительной корреляцией и при возрастании одной из них другая также возрастает. Если, то корреляция отрицательна и с ростом одной величины другая убывает. Можно доказать, что для любых двух случайных величинХ, Y

.

Если линейной зависимости нет, то . Если междуХиYсуществует функциональная линейная зависимость, топриипри. Заметим, чтоозначает только отсутствие линейной зависимости между случайными величинами; любой другой вид связи может при этом присутствовать.

Пример 6.5.

Закон распределения системы двух дискретных случайных величин (Х, Y) задан таблицей. Найти ковариациюсистемы и коэффициент корреляции.

Сделать вывод о тесноте зависимости между случайными величинами Х и Y.

Х У	1	2	4
0	0,1	0	0,1
2	0	0,3	0,3
5	0,2	0	0

Решение.

Ковариация вычисляется по формуле . Прежде всего найдем законы распределения дляХиY (п. 6.3).

Суммируя вероятности , стоящие в первом, затем во втором и третьем столбцах таблицы, получим:

.

Ряд распределения для Химеет вид

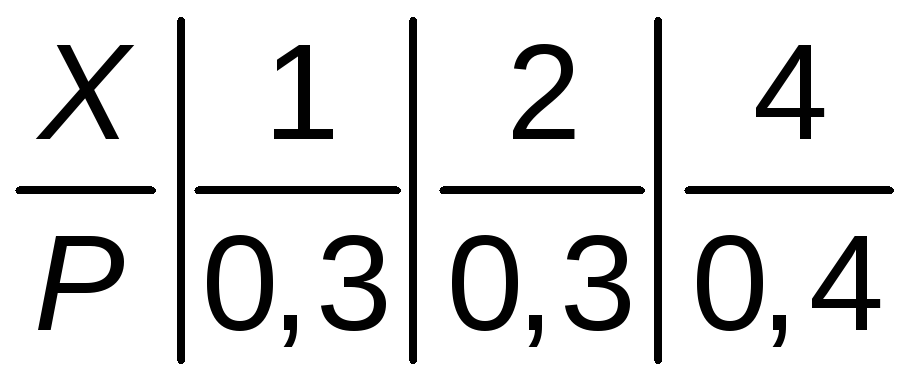
М(Х)=

D(X) = M(X- (M(X)).

.

D(X)= 7,9-(2,5).

Среднее квадратическое отклонение

Аналогично находим ряд для Y, суммируя вероятности по строкам таблицы:

.

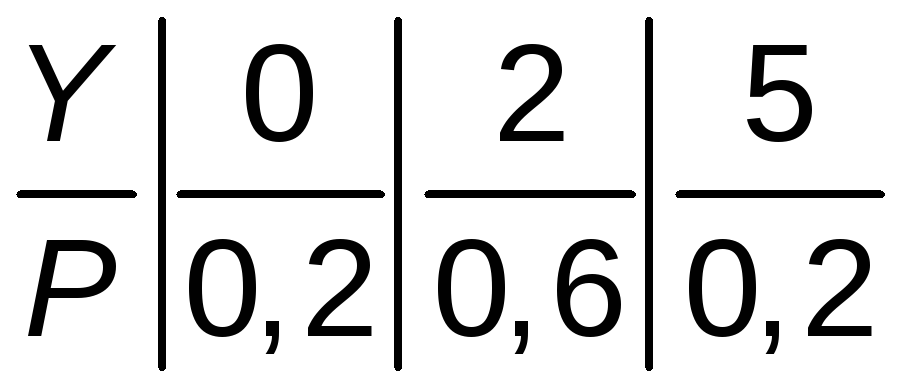M(Y)=.

Находим математическое ожидание произведения случайных величин Х и Y:

Ковариация сov(X,Y)= M(XY) – M(X)M(Y)= 4,6 – 2,5

Коэффициент корреляции определяется по формуле:

=.

Полученный результат говорит о том, что между случайными величинами Х и Y существует отрицательная линейная зависимость, т.е. при увеличении одной из них другая имеет некоторую тенденцию уменьшаться.