1.1.2. Бесповторные выборки

Представим себе, что имеется nкаких-то предметов, из которых нужно составить выборку объемаr. Выбор будем проводить по схеме:

– для выбора первого элемента имеется nспособов,

– для выбора второго элемента осталось n - 1способов,

– для выбора третьего элемента осталось n - 2 способа,

… … … … … … … … …

– для выбора k-го элемента осталосьn – r + 1способов.

Общее число способов, согласно комбинаторному принципу, равно произведению kсомножителей:n(n-1)(n-2)…(n-k+1). Такие комбинации встречаются часто и получили специальное название.

Размещениями изnэлементов поkназываются группы каких-тоkпредметов, взятых из этихnи отличающихся друг от друга либо составом, либо порядком их расположения в выборке. Таким образом, различными считаются размещения, в которых имеются или различные элементы, или, если все элементы одинаковы (одинаков состав), то различны порядки их расположения. Размещения изnэлементов поkобычно обозначаются символом

A = n(n-1)(n-2) … (n-k+1).

Пример 1.2.

В студенческой группе 25 студентов. Требуется выбрать актив группы, состоящий из трех человек. Сколько различных комбинаций при этом возможно?

Решение

В этом случае выборки будут отличаться друг от друга либо составом, либо порядком расположения. Действительно, при изменении порядка следования выбранная “тройка” займет уже другие посты. Следовательно, общее число способов дают размещения из 25 по 3 :

А= 252423 = 13 800.

Выясним, что получится при вычислении А. Пользуясь общей формулой для числа размещений, имеемА= n(n-1)(n-2)…321.

Размещения из nэлементов по n называютсяперестановкамиизnэлементов и обозначаются:= 123…n =n!.Символомn! (n – факториал)обозначается произведение всех целых положительных чисел от 1 доn. Очевидно, что приn2 справедливо следующее свойство:n! = (n-1)! n . Чтобы это равенство имело смысл при всех положительных целых значенияхn, по определению положим0! = 1.

Пример 1.3.

С помощью перестановок можно решать такие задачи: три человека могут сесть за парту в аудитории 3! = = 6 способами; десять человек встать в очередь или разместиться за столом может 10! различными способами (это число больше 3 млн).

Выясним теперь вопрос о том, сколько существует выборок объема rизn элементов, которые отличаются между собой хотя бы одним элементом. Группы изnэлементов поr, отличающиеся только составом, называютсясочетаниямиизnпоr. Число таких различных групп обозначается символомC. Получим формулу для подсчета всех возможных сочетанийC. Обратим внимание на то, что если наряду с каждым сочетанием рассматривать и все перестановки изrсоставляющих его элементов, то получим всевозможные размещения. Таким образом, выполняется равенство

,

отсюда

C=.

Преобразуем Ск более удобной для запоминания форме, для этого умножим числитель и знаменатель дроби на(n – r)!.

С=.

Из полученной формулы вытекает полезное равенство: С=С.

Пример 1.4.

От студенческой группы в 25 человек нужно послать трех представителей на студенческую конференцию. Сколько возникнет различных способов это сделать?

Решение

При выборе студентов важен только состав выборки, а порядок их расположения – нет. Следовательно, общее число способов будет равно

При решении задач комбинаторики можно придерживаться следующей схемы рассуждений:

1. Выяснить, какие группы образуют выборки – повторные или бесповторные.

2. В случае бесповторных выборок рассмотреть, чем они отличаются – только составом, порядком или тем и другим.

Классификация выборок представлена на рис. 1.1.

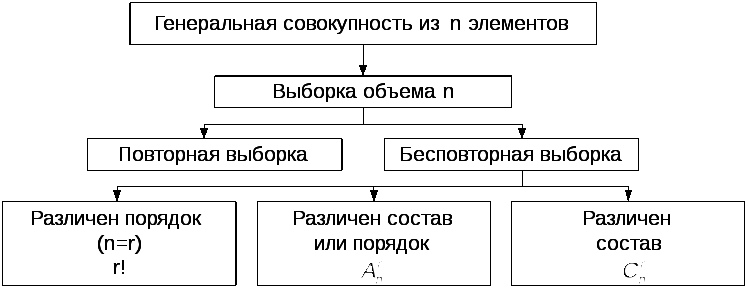
Рис. 1.1.