
- •Теория вероятностей
- •Введение
- •1. Случайные события. Вероятность событий
- •1.1. Элементы комбинаторики
- •1.1.1 Повторные выборки
- •Число способов выбора двух элементов
- •Число выборок из трех элементов
- •1.1.2. Бесповторные выборки
- •1.2. Основные понятия теории вероятностей
- •1.3. Алгебра событий
- •1.4. Частота события
- •1.5. Статистическое определение вероятности
- •1.6. Классическое определение вероятности
- •1.7. Свойства вероятностей
- •0Р(а)1.
- •1.8. Геометрические вероятности
- •1.9. Теорема умножения вероятностей. Условная вероятность
- •1.10. Теорема сложения вероятностей
- •1.10.1. Вероятность суммы событий
- •1.10.2. Вероятность появления хотя бы одного события
- •1.11. Формула полной вероятности. Формула Байеса
- •1.11.1. Формула полной вероятности
- •1.11.2. Вероятность гипотез. Формула Байеса
- •2. Повторные независимые испытания
- •2.1. Формула Бернулли
- •2.2. Формулы Лапласа
- •2.2.1 Локальная теорема Лапласа
- •2.2.2. Интегральная теорема Лапласа
- •2.3. Формула Пуассона
- •2.4. Простейший поток событий
- •3. Случайные величины
- •3.1. Понятие случайной величины
- •3.2. Законы распределения дискретных случайных величин
- •3.3. Законы распределения непрерывных случайных величин
- •3.3.1. Интегральная функция распределения
- •3.3.2. Показательный закон распределения
- •3.3.3. Дифференциальная функция распределения
- •3.3.4. Равномерное распределение
- •3.3.5. Распределение Коши
- •4. Числовые характеристики случайных величин
- •4.1. Математическое ожидание и его свойства
- •4.1.1. Математическое ожидание
- •4.1.2. Свойства математического ожидания
- •4.2. Дисперсия и среднее квадратическое отклонение
- •4.2.1. Дисперсия случайной величины
- •4.2.2. Свойства дисперсии
- •4.2.3. Среднее квадратическое отклонение
- •4.3. Моменты случайных величин
- •4.4. Примеры нахождения законов распределения
- •5. Нормальный закон распределения
- •5.1. Геометрический смысл параметров m и σ
- •5.2. Вероятностный смысл параметров функции распределения
- •5.3. Вероятность попадания случайной величины в заданный интервал
- •5.4. Вероятность отклонения случайной величины от математического ожидания
- •6. Системы случайных величин
- •6.1. Функция распределения
- •6.2. Плотность распределения
- •6.3. Закон распределения системы двух дискретных случайных величин
- •6.4. Зависимые и независимые случайные величины
- •6.5. Операции над случайными величинами
- •6.6. Числовые характеристики системы двух случайных величин
- •6.6.1. Ковариация двух случайных величин
- •6.6.2 Коэффициент корреляции
- •6.9. Двумерный нормальный закон распределения
- •7. Предельные теоремы теории вероятностей
- •7.1. Центральная предельная теорема
- •7.2. Интегральная теорема Лапласа
- •7.3. Распределение частоты события
- •7.4. Закон больших чисел
- •7.5. Неравенство Чебышева
- •7.6. Теорема Чебышева
- •7.7. Теорема Бернулли
- •7.8. Принцип практической уверенности
- •7.9. Правило трёх сигм
- •Контрольные вопросы
- •Заключение
- •Рекомендуемый Библиографический список
- •Теория вероятностей
- •680021, Г. Хабаровск, ул. Серышева, 47.
4.2.1. Дисперсия случайной величины
Дисперсией(рассеянием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
![]()
Для вычисления дисперсии можно использовать слегка преобразованную формулу
![]()
![]() ,
,
так как М(Х), 2 и![]() –
постоянные величины. Таким образом,
–
постоянные величины. Таким образом,
![]() .
.
4.2.2. Свойства дисперсии
Свойство 1.Дисперсия постоянной величины равна нулю. Действительно, по определению
![]()
Свойство 2.Постоянный множитель можно выносить за знак дисперсии с возведением его в квадрат.
Доказательство
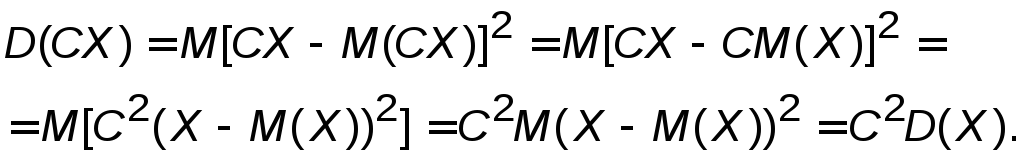
Центрированной случайной величиной называется отклонение случайной величины от ее математического ожидания:
![]()
Центрированная величина обладает двумя удобными для преобразования свойствами:
![]()
![]()
Свойство 3.Если случайные величины Х иYнезависимы, то
![]()
Доказательство. Обозначим![]() .
Тогда
.
Тогда![]() и
и![]() .
.
Поэтому
![]()
Во втором слагаемом в силу независимости случайных величин и свойств центрированных случайных величин
![]() ,
,
поэтому
![]() .
.
Пример 4.5. Еслиaиb– постоянные,
тоD(aХ+b)=D(aХ)+D(b)=![]() .
.
4.2.3. Среднее квадратическое отклонение
Дисперсия, как
характеристика разброса случайной
величины, имеет один недостаток. Если,
например, Х
– ошибка измерения имеет размерность
ММ,
то дисперсия имеет размерность
![]() .
Поэтому часто предпочитают пользоваться
другой характеристикой разброса –средним
квадратическим отклонением,
которое равно корню квадратному из
дисперсии
.
Поэтому часто предпочитают пользоваться
другой характеристикой разброса –средним
квадратическим отклонением,
которое равно корню квадратному из
дисперсии
![]()
Среднее квадратическое отклонение имеет ту же размерность, что и сама случайная величина.
Пример 4.6. Дисперсия числа появления события в схеме независимых испытаний
Производится nнезависимых испытаний и вероятность появления события в каждом испытании равнар. Выразим, как и прежде, число появления событияХчерез число появления события в отдельных опытах:
![]()
Так как опыты независимы, то и связанные
с опытами случайные величины
![]() независимы. А в силу независимости
независимы. А в силу независимости![]() имеем
имеем
![]()
Но каждая из случайных величин имеет закон распределения (пример 3.2)
|
|
0 |
1 |
|
Р |
1-р |
р |
и
![]() (пример 4.4). Поэтому, по определению
дисперсии:
(пример 4.4). Поэтому, по определению
дисперсии:
![]() ,
,
где q=1-p.
В итоге имеем
![]() ,
,![]()
Среднее квадратическое отклонение
числа появлений события в nнезависимых опытах равно![]() .
.
4.3. Моменты случайных величин
Помимо уже рассмотренных случайные величины имеют множество других числовых характеристик.
Начальным
моментом
k-го
порядка случайной величины Х
(![]() )
называется математическое ожиданиеk-й
степени этой случайной величины.
)
называется математическое ожиданиеk-й
степени этой случайной величины.
Центральным моментомk-го порядка случайной величиныХназывается математическое ожиданиеk-ой степени соответствующей центрированной величины.
![]()
Легко видеть, что центральный момент
первого порядка всегда равен нулю,
центральный момент второго порядка
равен дисперсии, так как
![]() .
.
Центральный момент третьего порядка дает представление об асимметрии распределения случайной величины. Моменты порядка выше второго употребляются сравнительно редко, поэтому мы ограничимся только самими понятиями о них.
4.4. Примеры нахождения законов распределения
Рассмотрим примеры нахождения законов распределения случайных величин и их числовых характеристик.
Пример 4.7.
Составить закон распределения числа
попаданий в цель при трех выстрелах по
мишени, если вероятность попадания при
каждом выстреле равна 0,4. Найти интегральную
функцию F(х)для
полученного распределения дискретной
случайной величиныХи начертить
ее график. Найти математическое ожиданиеM(X),
дисперсиюD(X)и среднее квадратическое отклонение
![]() (Х)
случайной величиныX.
(Х)
случайной величиныX.
Решение
1) Дискретная случайная величина Х– число попаданий в цель при трех выстрелах – может принимать четыре значения:0, 1, 2, 3. Вероятность того, что она примет каждое из них, найдем по формуле Бернулли при:n=3,p=0,4,q=1-p=0,6 иm=0, 1, 2, 3:
![]() .
.
Получим вероятности возможных значений
Х:![]() ;
;
![]() ;
;
![]() .
.
Составим искомый закон распределения случайной величины Х:
|
Х |
0 |
1 |
2 |
3 |
|
Р |
0,216 |
0,432 |
0,288 |
0,064 |
Контроль: 0,216+0,432+0,288+0,064=1.
Построим многоугольник распределения полученной случайной величины Х. Для этого в прямоугольной системе координат отметим точки (0; 0,216), (1; 0,432), (2; 0,288), (3; 0,064). Соединим эти точки отрезками прямых, полученная ломаная и есть искомый многоугольник распределения (рис. 4.1).
х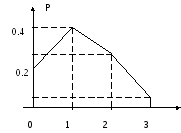
Рис. 4.1.
2) Если х![]() 0,
то F(х)=0.
Действительно, значений, меньших нуля,
величина Х
не принимает. Следовательно, при всех
х
0,
то F(х)=0.
Действительно, значений, меньших нуля,
величина Х
не принимает. Следовательно, при всех
х![]() 0
, пользуясь определениемF(х),
получим F(х)=P(X<x)=0
(как вероятность невозможного события).
0
, пользуясь определениемF(х),
получим F(х)=P(X<x)=0
(как вероятность невозможного события).
Если 0<x![]() ,
тоF(X)=0,216.
Действительно, в этом случаеF(х)=P(X<x)=
=P(-
,
тоF(X)=0,216.
Действительно, в этом случаеF(х)=P(X<x)=
=P(-![]() <X
<X![]() 0)+P(
0<X<x)=0,216+0=0,216.
0)+P(
0<X<x)=0,216+0=0,216.
Если взять, например, х=0,2, тоF(0,2)=P(X<0,2). Но вероятность событияХ<0,2 равна 0,216, так как случайная величинаХлишь в одном случае принимает значение меньшее 0,2, а именно0с вероятностью 0,216.
Если 1<x![]() ,
то
,
то
![]()
Действительно, Хможет принять значение 0 с вероятностью 0,216 и значение 1 с вероятностью 0,432; следовательно, одно из этих значений, безразлично какое,Хможет принять (по теореме сложения вероятностей несовместных событий) с вероятностью 0,648.
Если 2<x![]() ,
то рассуждая аналогично, получимF(х)=0,216+0,432 +
+ 0,288=0,936. Действительно, пусть, например,х=3. ТогдаF(3)=P(X<3)выражает вероятность событияX<3 –
стрелок сделает меньше трех попаданий,
т.е. ноль, один или два. Применяя теорему
сложения вероятностей, получим указанное
значение функцииF(х).
,
то рассуждая аналогично, получимF(х)=0,216+0,432 +
+ 0,288=0,936. Действительно, пусть, например,х=3. ТогдаF(3)=P(X<3)выражает вероятность событияX<3 –
стрелок сделает меньше трех попаданий,
т.е. ноль, один или два. Применяя теорему
сложения вероятностей, получим указанное
значение функцииF(х).
Если x>3, тоF(х)=0,216+0,432+0,288+0,064=1.
Действительно, событиеX![]() является
достоверным и вероятность его равна
единице, аX>3 –
невозможным. Учитывая, что
является
достоверным и вероятность его равна
единице, аX>3 –
невозможным. Учитывая, что
F(х)=P(X<x)=P(X![]() 3)
+ P(3<X<x),
получим указанный результат.
3)
+ P(3<X<x),
получим указанный результат.
Итак, получена искомая интегральная функция распределения случайной величины Х:
F(x)=![]()
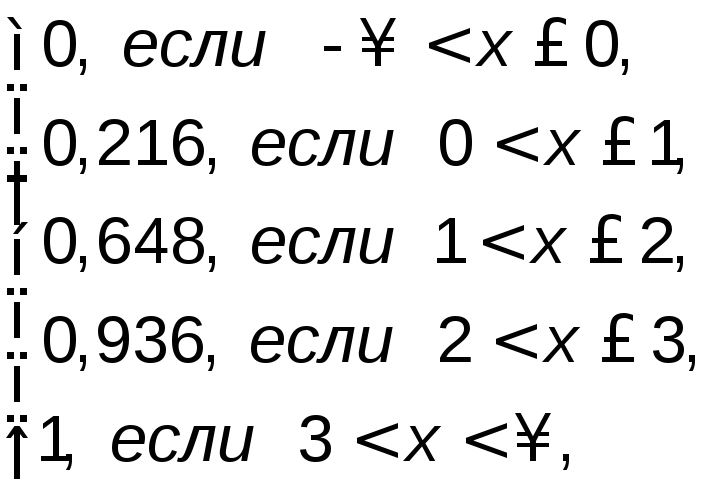
график которой изображен на рис. 4.2.
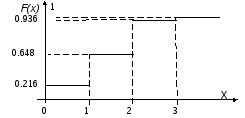
Рис. 4.2
3) Математическое ожидание дискретной случайной величины равно сумме произведений всех возможных значений Хна их вероятности:
М(Х)=0![]() =1,2.
=1,2.
То есть, в среднем происходит одно попадание в цель при трех выстрелах.
Дисперсию можно вычислить, исходя из
определения дисперсии D(X)=M(X-M(X))![]() или воспользоваться формулойD(X)=M(X
или воспользоваться формулойD(X)=M(X![]() ,
которая ведет к цели быстрее.
,
которая ведет к цели быстрее.
Напишем закон распределения случайной
величины Х![]() :
:
|
Х2 |
0 |
1 |
4 |
9 |
. |
|
Р |
0,216 |
0,432 |
0,288 |
0,064 |
Найдем математическое ожидание для Х![]() :
:
М(Х![]() )= 0
)= 0![]() 4
4![]() = 2,16.
= 2,16.
Вычислим искомую дисперсию:
D(X)
= M(X![]() )
– (M(X))
)
– (M(X))![]() = 2,16 – (1,2)
= 2,16 – (1,2)![]() = 0,72.
= 0,72.
Среднее квадратическое отклонение найдем по формуле
![]() (X)
=
(X)
=
![]() = 0,848.
= 0,848.
Интервал (M-![]() ;
M+
;
M+![]() )
= (1,2-0,85; 1,2+0,85) = (0,35; 2,05) – интервал
наиболее вероятных значений случайной
величиныХ, в него попадают значения
1 и 2.
)
= (1,2-0,85; 1,2+0,85) = (0,35; 2,05) – интервал
наиболее вероятных значений случайной
величиныХ, в него попадают значения
1 и 2.
Пример 4.8.
Дана дифференциальная функция распределения (функция плотности) непрерывной случайной величины Х:
![]() f(x)=
f(x)=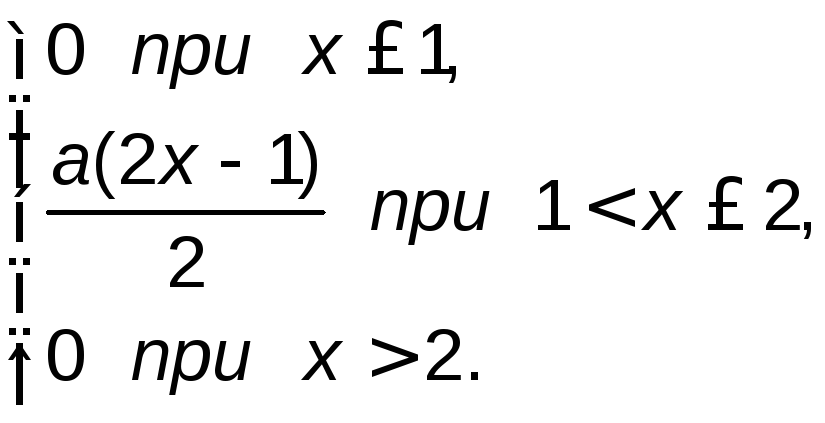
1) Определить постоянный параметр a.
2) Найти интегральную функцию F(x).
3) Построить графики функций f(x)иF(x).
4) Найти двумя способами вероятности
Р(0,5<X![]() 1,5)иP(1,5<X<3,5).
1,5)иP(1,5<X<3,5).![]()
5). Найти математическое ожидание М(Х),
дисперсиюD(Х)и
среднее квадратическое отклонение
![]() случайной величиныХ.
случайной величиныХ.
Решение
1) Дифференциальная функция по свойству
f(x)должна удовлетворять условию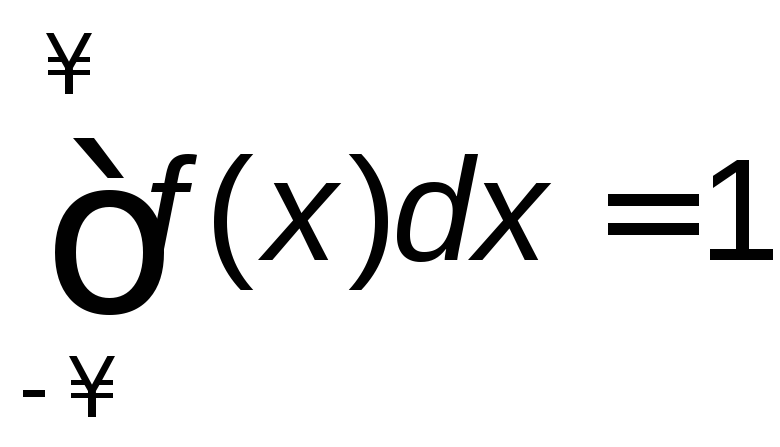 .
.
Вычислим этот несобственный интеграл для данной функции f(x):
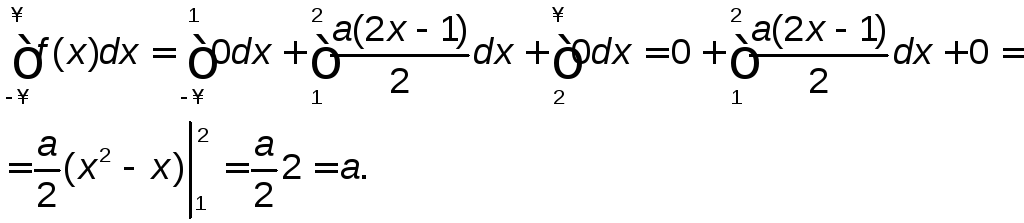
Подставляя этот результат в левую часть
равенства, получим, что а=1. В условии
дляf(x)заменим параметрана 1:![]()
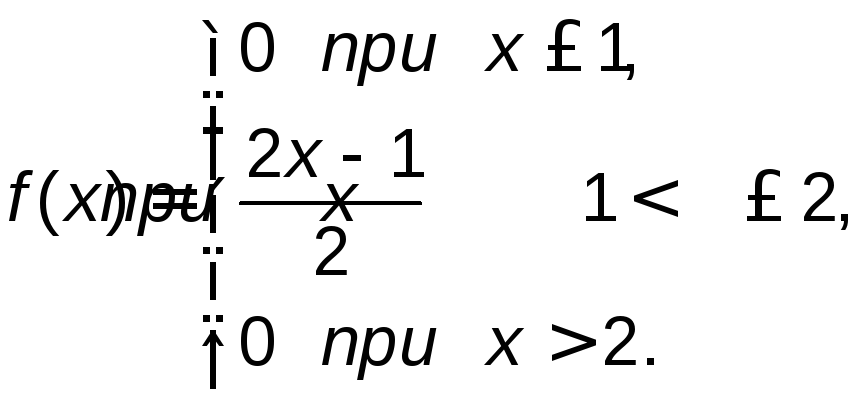
2) Для нахождения F(x)воспользуемся формулой
 .
.
Если х![]() ,
то
,
то![]() ,
следовательно,
,
следовательно,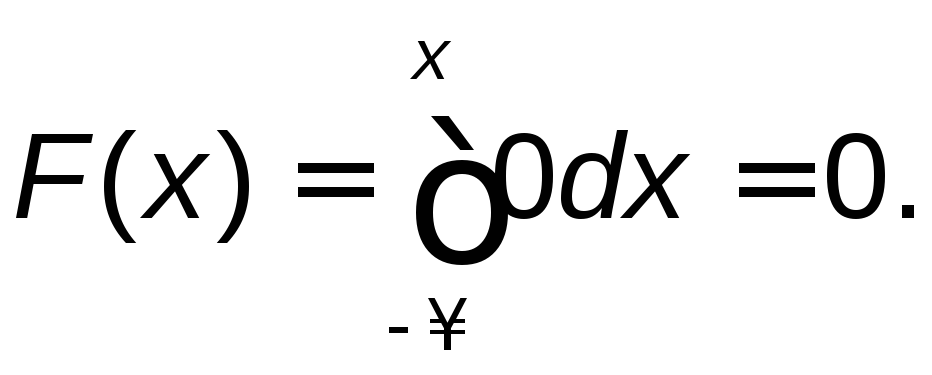
Если 1![]() то
то
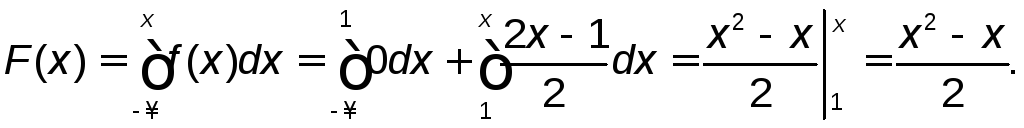
Если x>2, то
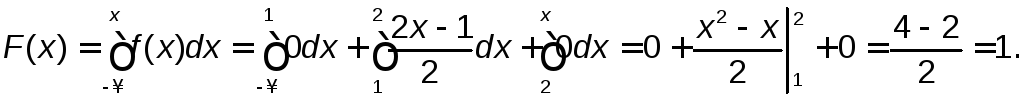
Итак, искомая интегральная функция F(x)имеет вид:
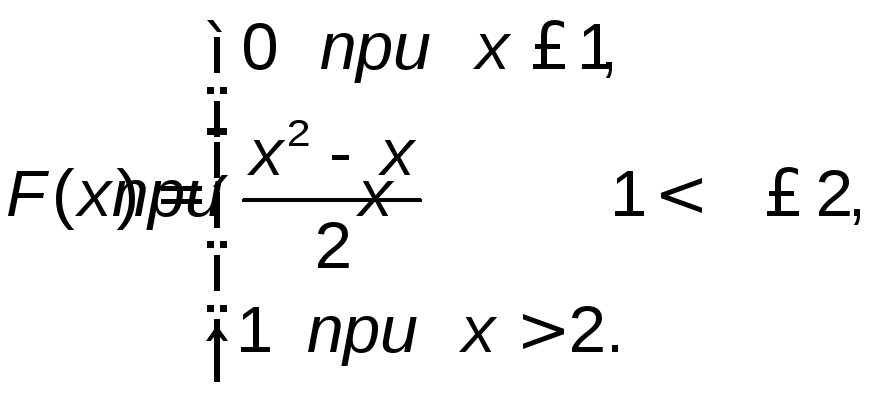
3) Построим графики функций f(x)иF(x) (рис. 4.3 и 4.4).

Рис. 4.3
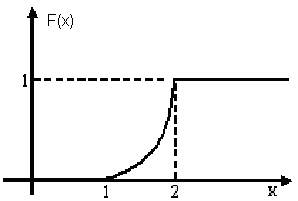
Рис. 4.4.
4) Вероятность попадания случайной
величины в заданный интервал (а,b)вычисляется по формуле
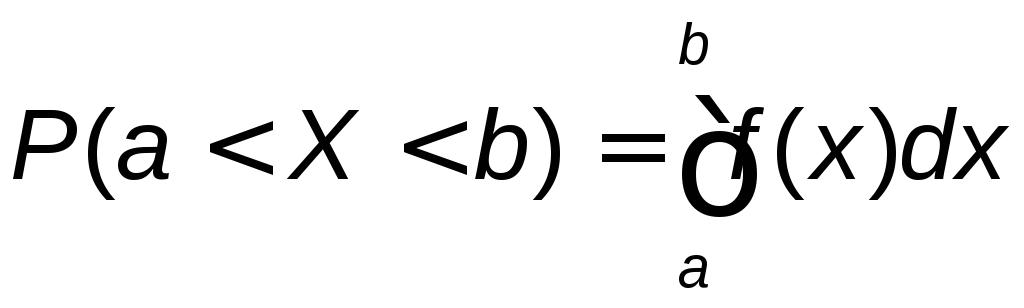 ,
если известнафункция
f(x),
и по формуле P(a
< X
<b)
= F(b)
– F(a),
если известна
функция F(x).
,
если известнафункция
f(x),
и по формуле P(a
< X
<b)
= F(b)
– F(a),
если известна
функция F(x).
Найдем
![]() по двум формулам и сравним результаты.
По условиюа=0,5; b=1,5;
функцияf(X)
задана в пункте 1). Следовательно,
искомая вероятность по формуле равна:
по двум формулам и сравним результаты.
По условиюа=0,5; b=1,5;
функцияf(X)
задана в пункте 1). Следовательно,
искомая вероятность по формуле равна:
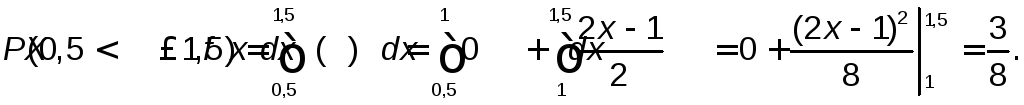
Та же вероятность может быть вычислена по формуле b) через приращение полученной в п.2). интегральной функцииF(x)на этом интервале:
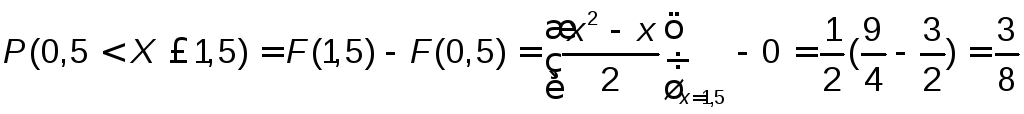 ,
так какF(0,5)=0.
,
так какF(0,5)=0.
Аналогично находим![]()
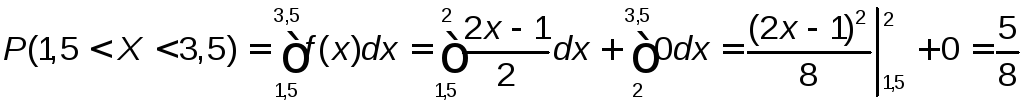 ,
,
или
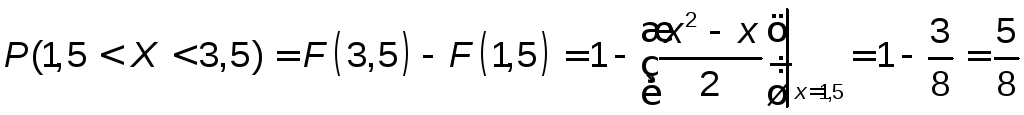 ,
,
так как F(3,5)=1.
5) Для нахождения математического
ожидания М(Х)воспользуемся формулой
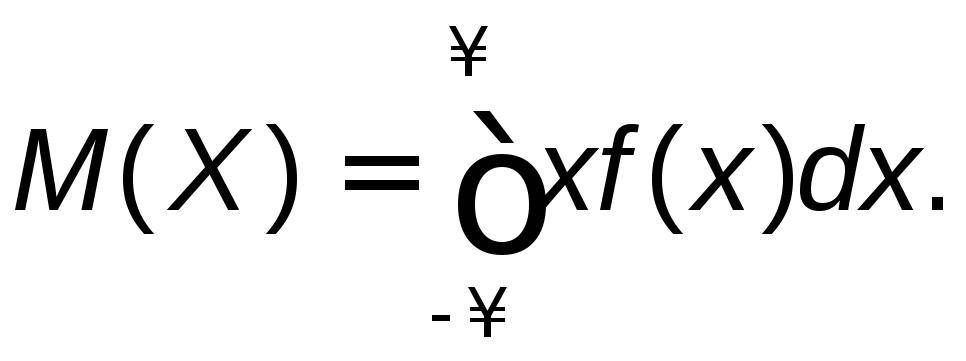 Функцияf(x)
задана в решении пункта 1), она равна
нулю вне интервала (1,2]:
Функцияf(x)
задана в решении пункта 1), она равна
нулю вне интервала (1,2]:
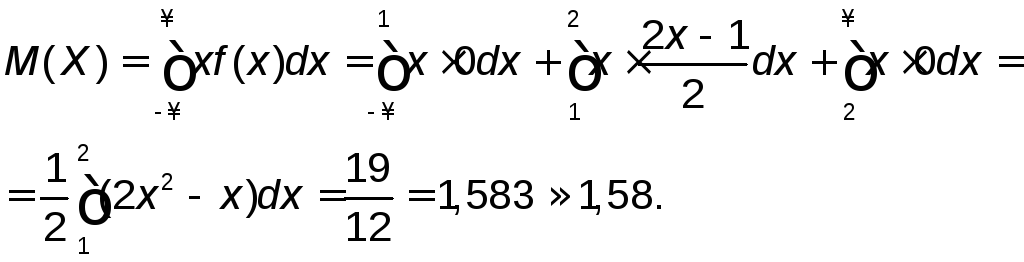
![]() Дисперсия
непрерывной случайной величиныD(Х)определяется равенством
Дисперсия
непрерывной случайной величиныD(Х)определяется равенством
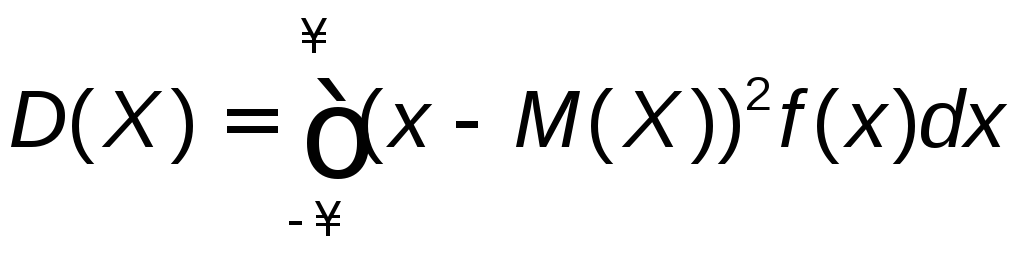 ,
или равносильным равенством
,
или равносильным равенством
![]()
 .
.
Для![]() нахожденияD(X)воспользуемся последней формулой и
учтем, что все возможные значенияf(x)принадлежат интервалу (1,2]:
нахожденияD(X)воспользуемся последней формулой и
учтем, что все возможные значенияf(x)принадлежат интервалу (1,2]:
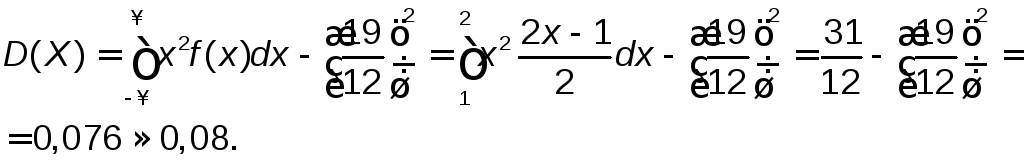
Среднее квадратическое отклонение
![]() =
=![]() =0,276.
=0,276.
Интервал наиболее вероятных значений случайной величины Хравен
(М-![]() ,М+
,М+![]() )
= (1,58-0,28; 1,58+0,28) = (1,3; 1,86).
)
= (1,58-0,28; 1,58+0,28) = (1,3; 1,86).
