Распределение Вейбулла

Таблица 20

Интервальные оценки показателей надежности

при законе распределения Вейбулла для малых выборок (N≤15)

Показатель надежности	Доверительная граница при доверительной вероятности q
	Нижняя граница	Верхняя граница
Средняя наработка до отказа (на отказ), средний ресурс (срок службы, срок сохраняемости, время восстановления)
Гамма – процентная наработка до отказа, гамма – процентный ресурс (срок службы, срок сохраняемости)
Вероятность безотказной работы за наработку t		—

Примечания:

1. Значения функций V_qиV_q^γприведены в таблицах.

2. Для плана [NUz]значенияV_qиV_q^γнаходят дляr = [N(1-P(t_r)].

3. Значения P(t_r)находят интерполяцией между значениямиγ₁иγ₂.

Оценка остаточного ресурса по результатам испытаний

Задача оценки остаточного ресурса актуальна по той причине, что расчётный ресурс, как правило, определен с запасом. Техническое устройство, таким образом, может эксплуатироваться и после исчерпания назначенного ресурса. Поэтому, с точки зрения эффективности использования, целесообразно иметь более реалистичные данные о ресурсе технического устройства (см. также ПЗ 4).

Точечная оценка среднего остаточного ресурса по результатам испытаний Nобъектов, достигших предельного состояния, определяется выражением:

где N- объем выборки,τ- наработка, для которой определяется остаточный ресурс,k- количество отказавших объектов на интервале наработки (0,τ).

Формулы для расчета доверительных границ остаточного ресурса приведены в справочниках.

ПРИМЕР 28

Определить средний остаточный ресурс объекта после наработки 10 000 часов при условиях: Испытано 10 объектов. Их наработки до отказа составили: 250, 12050, 12500, 14100, 14450, 16050, 17100, 18950, 19200, 19700 часов.

P.S.Если бы мы оценивали по тем же испытаниям среднюю наработку до отказа непараметрическим методом, то она была бы равна:

=14440 ч., а у нас уже получилось не менее 10000+6011=16011 ч.

Оценка показателей безотказности при испытаниях с измерением определяющих параметров

Особым разделом определения показателей надежности по результатам испытаний является оценка их по измерениям, так называемых, определяющих параметров. В процессе испытаний или эксплуатации измеряют некоторые параметры, характеризующие как сам объект, так и условия его работы. В результате измерений значения параметров сравнивают с заданными пределами их изменений. По близости к этим пределам или по их превышению оценивают вероятность безотказной работы в требуемом интервале времени. Теоретическое обоснование и формулы для расчета точечных и интервальных оценок показателей надежности по этому методу приведены в справочниках.

Рассмотрим применение этих методов на нескольких примерах.

ПРИМЕР 29

Пусть определяющим параметром является электрическая прочность изоляции. Напряжение пробоя согласно ТУ должно быть больше а= 360 кВ после наработкиt₀. По результатам испытанийN = 4 образцов при заданной наработке получены следующие значения напряжения пробоя: 720, 840, 970 и 1040 кВ. Нужно оценить вероятность безотказной работы (точечную оценку среднего значения и ее нижнюю доверительную границу при доверительной вероятности 0,9) изоляции за заданную наработку при нормальном законе распределения напряжения пробоя.

По выборочным данным x_i(i=1...N) находят оценки параметров распределения по соотношениям:

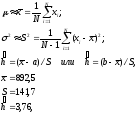
где aиb– нижний и верхний пределы допуска соответственно, аh– нормируемый допуск.

Точечную оценку вероятности безотказной работы находят из выражения:

по таблицам функции Лапласа для данной оценки нормируемого допуска получаем:

По значениям: N = 4,h= 3,76 для доверительной вероятностиγ= 0,9 по таблицам доверительных границ находим:

ПРИМЕР 30

Требуется оценить вероятность безотказной работы (при доверительной вероятности γ=0,9) осветительной ракеты, работоспособное состояние которой характеризуется нахождением в границах допусков таких определяющих параметров: сила светаХ₁, время работыХ₂и скорость вылетаХ₃. Заданы следующие границы допусков:Х₁> a₁, a₁=1000Кд; Х₂> a₂, a₂=20с; а₃<X₃<b₃, a₃=15 м/с, b₃=20 м/с.

Проведены испытания образцов. Их результаты таковы: По 9-и образцам (N1=9) определяли силу света: МХ1=1084Кд, S1=28,3. По 12-и образцам (N2=12) определяли время работы: МХ2=22,4с, S2=0,8. По 9-и образцам (N3=9) определяли скорость вылета: МХ3=18,6м/с, S3=1,19.

Предполагается нормальный закон распределения для всех определяющих параметров.

Вероятность безотказной работы:

Обозначения те же, что и в предыдущем примере.

Если заданы односторонние допуски, то М=m- числу определяющих параметров. Если заданы двусторонние допуски, тоМ=2 m. В нашем примереМ=4, так как один из трех допусков задан двусторонним.

h₁...h₄равны 2,97; 2,99; 3,04; 2,89 соответственно. По таблицам для нормального распределения находим:

Для N=min(9; 12; 9)=9 и доверительной вероятностиγ=0,9 по таблицам находим:

Рассмотренные два примера относятся к так называемым статическим допусковым моделям надежности. Это означает, что заданы пределы допусков на изменения определяющих параметров. Если же задаются условия непревышения параметром заданного значения, то такие модели называются статическими моделями непревышений или «нагрузка – прочность» (нагрузка в каждый момент времени должна быть ниже предела прочности). В отличие от допусковых моделей, в моделях непревышений нормированный допуск вычисляется как разница двух случайных величин со своими распределениями: одна из них – прочность, вторая – нагрузка. Соотношения для определения нормированного допуска и вероятности безотказной работы имеют вид:

Кроме статических существуют, так называемые, динамические модели отказов. В этих моделях помимо условия нахождения в допуске или непревышения заданного уровня присутствует условие по длительности процесса (анализируемый интервал работы). В отличие от этого в статических моделях не рассматривается зависимость определяющего параметра от времени/наработки. Математическая запись такой модели выглядит следующим образом:

A(t₀)– событиеAв моментt₀.

Показатель безотказности имеет вид:

D–допустимая область изменения определяющего параметра (односторонняя или двухсторонняя):

Динамические модели применяются в случаях, когда определяющий параметр меняется во времени. Например, глубина коррозии стенки трубопровода. В динамической модели должна быть известна закономерность изменения определяющего параметра на заданном интервале времени.

Рассмотрим в качестве примера схему статистической оценки безотказности при измеряемых реализациях определяющего параметра.

В ходе испытаний производятся наблюдения за реализациями определяющего параметра (или нескольких параметров). Модель зависимости параметра от времени имеет канонический вид:

где φ_ι- монотонные функции на промежутке [0,t₀], выбранные заранее, линейно независимые.

вектор случайных коэффициентов, нормально распределенных с неизвестным средним значением:

и дисперсией вида σ²θ, гдеσ²- неизвестный множитель,θ- известная симметричная положительно определённая матрица размера (k,k).

Для модели изменения параметра X(t)=α₁+α₂t, φ₁(t)=1, φ₂(t)=t и

где К₁₂=К₂₁– коэффициенты ковариацииα₁иα₂. Всеθ_ijзаранее известны.

При монотонно возрастающем определяющем параметре вероятность безотказной работы находят по функции Лапласа Ф:

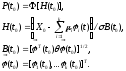
Для нашего случая линейной модели: