
- •Частные производные функции n-переменных.
- •Производная по направлению и градиент функции n-переменных
- •Поверхность уровня функции n-переменных.
- •Дифференцирование сложных функций.
- •Формула Тейлора
- •Экстремум функции n-переменных
- •Задача Условного Экстремума
- •Понятие о задаче оптимизации.
- •Дифференциальные уравнения.
- •1.1Основные понятия.
- •Дифференциальные уравнения первого порядка.
- •Некоторые сведения об особых решениях.
- •Уравнения второго порядка, допуск понижения.
- •Линейные уравнения первого порядка.
- •Линейные однородные дифференциальные уравнения n-ого порядка с постоянным коэффициентом.
- •Линейные неоднородные дифференциальные уравнения n-ого порядка.
- •Системы дифференциальных уравнений – несколько уравнений взятых вместе.
- •Линейные однородные системы
- •Устойчивость линейной системы. Точки покоя.
- •Кратные интегралы
- •Замена переменной в двойном интеграле
- •Поверхностные интегралы.
Конспект Лекций по Математике 4
Теория функций нескольких переменных
Дифференцированные функции
Кратные интегралы
§1
Понятие об n-мерном пространстве. И о функции нескольких переменных
Определение:
n-мерной точкой называется любая упорядоченная совокупность из n вещественных чисел
М=(х1,х2,...,хn).
числа
Указанные числа часто называют координатами точки .
М=(3;2;-1;0)- четырёх мерная точка.
Множество всех n- мерных точек называется n- мерным координатным пространством
n-мерное координатное пространство называется n- мерным Евклидовым пространством, если для любых двух точек этого пространства существует расстояние между ними
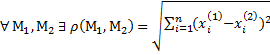
Расстояние
Евклидово пространство Еn
М1=(1;2;4;0)
М2=(-1;0;3,5)
![]() =
=![]() =
=![]()
В n-мерном пространстве вводятся следующие важные множества:
1)Открытый n-мерный шар радиусом R с центром в точке М0
{M}
![]() Еn
:
Еn
:![]() М
М ![]() <R
<R
 х2
х2
 М0
М0
х1
2) Закрытый n-мерный шар
{M} Еn : М ≤R
х 2
2
М0
х1
3)n-мерная сфера
{M} Еn : М =R
х 2
2
R
M0
Х1
М-внутренняя точка {M} Еn

 х2 М
х2 М
М0
х1
5)М0-внешняя точка множества {M} Еn
Существует такой n- мерный шар, который не принадлежит множеству М.
 х2
х2
 М0
М0
М
х1
5) М0 – Граничная точка {M} Еn
х
 2
2


 М0
М0
М
 х1
х1
7) Множество всех граничных точек называется границей множества М
8)Множество М n-мерного пространства называется открытым, если все его точки внутренние.
 х2
х2
М
х1
9) Множество М называется закрытым, если в него входит ещё и его граница.
10) Множество М называется ограниченным, если оно целиком содержится в некотором n-мерном шаре.
х 2
2
М
х1
11)Множество М называется неограниченным, если в никакой шар оно не влезает.
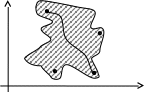
12) {M} Еn – называется связные если любые две его точки можно соединить непрерывной кривой целиком лежащей в этом множестве.
 х2
х2
 L
L
M
х1
х




 2
2
Не связная
х
13)Множество называется выпуклым, если любые две его точки можно соединить n- мерным отрезком, целиком лежащим в этом множестве.
х



 2
2
Не выпуклое
х1
х 2





х1
14) n-мерной областью называется открытое связное множество n-мерного пространства.
15) Uɛ(М0) (эпсилон окрестностью n-мерной точки М0)-называется n-мерный шар радиуса ɛ(эпсилон) с центром в точке М0.
Определение:
Пусть в n-мерном пространстве дана некоторая область D Еn если каждой n-мерной точке области D по некоторому правилу f ставится в соответствие некоторое число z, то говорят что в области D задана функция n-мерных точек или функция n-переменных и обозначают:
D
Еn
![]() М
М![]() D
D![]() z
R
z
R
Z=![]() (М)
или z=f(х1,х2,
х3,...,хn)
(М)
или z=f(х1,х2,
х3,...,хn)

 D
D

 М
f
М
f
Z= (М
Еn
Областью D называют областью определения функции.
Задаются функции n-мерных переменных как правило аналитически- формулой содержащей координаты n-мерной точки.
Пример:
z=![]() Внешность четырехмерного
шара + четырехмерная сфера
Внешность четырехмерного
шара + четырехмерная сфера
D(z):
![]()
![]()
z=ln(х1+х2+ х3-5)
D(z): х1+х2+ х3>5- трёхмерное полупространство без плоскости.
Графиком функции n-переменных является поверхность в n+1 мерном пространстве .
Графически можно проиллюстрировать только функцию двух переменных. Её графиком является обычная поверхность в трехмерном пространстве.
Пример:
z=![]()
D (z):
(z):![]() ≤
9 R=3
≤
9 R=3


 x3(z)
x3(z)




 z=
z=









 3
D 3
3
D 3
х1 х2
z=![]()
D (z):x1Ox2 х3
(z):x1Ox2 х3













z
 =
=
х1 х2
§2
Предел и непрерывность функции n-переменных.
Определение предела и непрерывности функции n-переменных формально ничем не отличается от случая функции одной переменной.
lim
f(M)=A
Uɛ(A)
![]() (M0):
(M0):
![]() M
M
![]() (М0)
f(M)
Uɛ(A)
(М0)
f(M)
Uɛ(A)
MM0
f(M) непрерывна в точке M0 lim f(M)= f(M0)
MM0

х2


M
х1
Для функции n-переменных теряет смысл теорема об односторонних пределах. О существовании предела можно говорить тогда, и только тогда, когда его значение не зависит от пути стремления точки М, к точке М0, а таких пути всегда бесконечно много.
На первый план выходит задача не о вычислении предела, а о его существовании.
Даже в простейших примерах могут возникнуть трудности.
Пример:
z=![]() М0(0;0)
М0(0;0)
lim![]() =
=![]()
MM0


 x2
x2
 M
M
x2=kx1
x
 1
1
lim![]() =
= ![]()
x10
Значение предела зависит от пути предела или вообще
Поскольку условие существования предела очень жёсткие- все понятия связаны с пределом усложняются именно с точки зрения непрерывности, дифференцирования и интегрирования.
Все основные теоремы о пределах и непрерывностях сохраняются, но каждый раз надо требовать существования всех предельных переходов.
Например, при изучении непрерывности функции может быть непрерывна по каждой переменной в отдельности, но иметь разрыв по совокупности переменных.
§3
Частные производные функции n-переменных.
Пусть функция n-переменных задана в некоторой области D n-ого пространства, пусть координаты имеют вид.
z=f(M):
D
![]() Еn,
М- внутренняя точка. M0(
Еn,
М- внутренняя точка. M0(![]() )
)
Придадим независимое приращение координате х1, а остальные координаты оставим без изменения
Назовём частным приращением по координате х1 следующую разность:
Δ
х1
f(M0)=
f(![]() +
Δ х1
+
Δ х1![]() )-
f(M0)
)-
f(M0)
Частной производной по переменной х1 назовём следующее соотношение:
lim![]()
Δ х10
Обозначается частная производная следующим образом:

f'’
=
z’
или ![]()
x1 M0 x1 M0 M0
Абсолютно аналогично можно ввести частную производную по любой переменной:
f'’x2 , f'’ x3 ,… , f'’ xn
Каждая частная производная характеризует скорость изменения функции вдоль соответствующей координатной оси.
Все правила взятия производных остаются в силе.
z=arctg(x1+x12)
z’x1=![]() 1,
z’x2=
2 x2,
1,
z’x2=
2 x2,
§4
Дифференцируемость функций n-переменных. Линеаризация функций.
Пусть функция n-переменных задана в некоторой области D n-ого пространства, точка М0 внутренняя точка. Придадим независимое приращение каждой координате точки М0.
M0=
(
,![]() )
)
Δ х1 Δ х2 Δ хn
Получим новую точку M1
M0=
(
+
Δ х1,![]() )
)
Назовём полным приращением функции в точке M0 следующую разность:
Δf(M0)= f(M1) -f(M0)
Функция z= f(M)- называется дифференцируемой в точке M0, если справедливо следующее соотношение:
 Расстояние
Расстояние
Δf(M0)=![]() +о(
+о(![]() M0,
M1))
«о» более высокого порядка, чем
M0,
M1)
M0,
M1))
«о» более высокого порядка, чем
M0,
M1)
 М1М
М1М
Полн. Сумма.
Приращ. Слагаем.
Относит.
Приращ.
Оргум. Δ хi
![]() =const
=const
Теорема (необходимое условие дифференцируемости)
Если функция дифференцируема в точке M0, то в этой точке существуют все частные производные при этом:
A 1=
f '
;
A2=
f '
,…,
An=
f '
1=
f '
;
A2=
f '
,…,
An=
f '
x1 M0 x2 M0 xn M0
Теорема (достаточное условие дифференцируемости)
Если у функции в точке M0 и её окрестности существуют все частные производные, при чём они непрерывны в точке M0, то функция дифференцируема в точке M0.
Определение:
Сумма слагаемых линейных относительно приращения аргументов в основном соотношении называется полным дифференцированием в точке M0 и обозначается df(M0).

Если
z=
f(M)
дифференцируема в точке M0
,то df(M0)![]()
![]()
xi M0
Замечание:
Как и для функции одной переменной приращения независимых переменных отождествляют с их дифференциалами:
![]() =
d
=
d![]() ;
;![]() =
d
=
d![]() ;
;![]() =
d
=
d![]()

df(M0)=![]()
![]()
xi M0
Если приращение аргументов невелики (работаем в окрестности точки M0), о- малое можно не замечать
о ( M0, M1)), тогда справедливо приближённая формула:
![]() f(M0)
f(M0)![]() df(M0)
df(M0)


f(M)![]() +d
f(M0)
M
U(M0)
+d
f(M0)
M
U(M0)
![]() f(M0)+
(xi
- xi0)
в U(M0)
f(M0)+
(xi
- xi0)
в U(M0)
xi M0
Можно назвать линеаризацией функции в области точки M0
Пример:
z=x1 x22+x2 x32+ x13
M0=(1,2,3)
z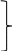 ’x1=x22+3x12
’x1=x22+3x12
z’x2=2x1x2+x32 непрерывна
в U(M0)
z=![]() -
дифференцируема в точке
M0
-
дифференцируема в точке
M0
z’x3=2x2x3

z’ =7; z’ =13; z’ = 12.
x1 M0 х2 M0 х3 M0
df(M0)=
7d
+13d
+12d![]() =7(
-1)+13(
=7(
-1)+13(![]() +12(
+12(![]()
f(M0)=23
f(M)
23+7(![]() )+13(
+12(
,
в U(M0)
)+13(
+12(
,
в U(M0)
§5
