Формула Тейлора
Отметим:
Формулировка формулы Тейлора для многомерного случая ничем не отличается от случая одной переменной, если записать формулу Тейлора через дифференциалы.
Пусть функция z=f(M) m+1 раз дифференцируема в окрестности точки M0, тогда справедлива формула Тейлора:
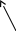
f(M0)=
+о(
M,
M0))
M
M0 MM0
п
олное
приращение
M0
M,
M0))
f(M)-
f(M0)
Пример:
z=f(M)=sin(x1-x2)
Написать формулу Тейлора до второго порядка
В качестве M0: M0(0;0)
sin(x1-x2)-
sin(0-0)=
+
+ о(
x1,
x2),
M0(0;0))
M0 M0 M (0;0)
=
d
x1+
d
x2=
( x1-
x10)+
(
x2-
x20)=cos(x1-x2)
(
x1-
x10)+
M0 M0
+(-cos(x1-x2) ( x2- x20))=1*x1-1*x2
M0
=
(d x1)2+2
d
x1d
x2+
(d x2)2=
(x1-
x10)2+2
(
x1-
x10)
( x2-
x20)+
M0
+ (x2- x20)2=-sin(x1-x2)2 (x1- x10)2+2sin(x1-x2) ( x1- x10) ( x2- x20)+(-sin(x1-x2)2 (x2- x20)2=
M0 M0
0*x12+2*0*
x1*x2+0*x22
Формула Тейлора и того:
sin(x1-x2)=
+
+
,
М0))
§10
Экстремум функции n-переменных
Определение экстремума функции n-переменных принципиально ничем не отличается от определения для функций одной переменной.
Необходимое условие экстремума.
Отметим:
Функцию f(M) будем считать, по крайней мере, дважды дифференцируемой.
Если в точке М0 есть экстремум, то все частные производные обращаются в ноль (градиент в точке М0 становится нулевым вектором)
Точки подозрительные на экстремум называется стационарными.
Достаточное условие экстремума.
Отметим:
Смена знаков производных, при переходе через стационарную точку для многомерного случая не работает.
Наличие или отсутствие экстремума в стационарной точке зависит от поведения второго дифференциала в этой точке, как квадратичной формы от приращения переменных.
Теорема:
П усть точка М0 стационарная точка функции. Если:
1)Второй дифференциал в точке М0 больше нуля, то точка М0 – точка минимума. >0 => точка М0-точка min
М0
2)Второй дифференциал всегда меньше нуля, то точка М0 – точка максимума. < 0 => точка М0-точка max
М0
3 )Второй дифференциал то больше нуля то меньше нуля, то в точке М0 нет экстремума.
то>0,то< 0 =>в точке М0 нет extr
М0
4 )Второй дифференциал больше нуля, но иногда равен нулю (меньше нуля, но иногда равен нулю)
>0 ,но иногда = 0 (< 0, но иногда = 0) ( неизвестно есть экстремум, или нет)
М0
Отметим:
Исследовать - напрямую достаточно сложно, поскольку приращение аргументов бесконечно много.
Для случаев 1) и 2) есть удобная методика, но для 3) и 4)
Определение:
Матрицей Гессе называется следующая квадратная матрица:
)nxn
– эта матрица всегда симметрична
относительно главной диоганали.
М0
Главным минором этой матрицы называются миноры, примыкающие к левому верхнему углу.
Если:
1)Все главные миноры строго больше нуля, то второй дифференциал тоже больше нуля, и в точке М0 минимум.
2)Главные миноры чередуют знак (-+-+-+) то главный дифференциал меньше нуля и в точке М0 максимум.
Замечание:
Для случая двух переменных матрица может дать ответ и в случае 3) и 4):
3)Если второй главный минор меньше нуля, то экстремума нет.
4)Если второй главный минор равен нулю, то? (ничего неизвестно)
Пример:
z=x13+x23-3x1 x2
Найти экстремумы
1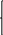
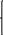)Необходимое
условие экстремума.
,
3x12-3x2=0
стационарная точка М1(1;1) М2(0;0)
,
3x22-3x1=0
2)Достаточное условие экстремума.
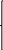
=> A
а) М1(1;1)
точка М1-
точка локального минимума.
б) М1(1;1)
экстремума нет
Отметим:
Разновидностью экстремальных задач является две часто встречающиеся задачи:
1)Задача Условного Экстремума (ЗУЭ)
2)Задача Оптимизации (ЗО)
§11