Уравнения второго порядка, допуск понижения.
1.Уравнение только с х:
=> два раза проинтегрировать.
2.Уравнение без у:
F(x,y’,y’’)=0
Замена: у’=P(x), y’’=P’(x)
3.Уравнение без х:
F(у,y’,y’’)=0
Замена: у’=P(у), y’’=P’(у)
Замечание:
Если для указанного уравнения решить задачу Коши, то производная постоянных лучше находить не в конце решения, а в процессе - упрощает взятие интеграла.
Пример:
;
;
;
-
решение задачи Коши.
y
1 
x
2)
, 
,
н
ет
у=> 
,
x
–Линейное уравнение
P
=UV
I
.
II.
,
Найдём
:
Ответ:
– частное решение
3)
=> по начальным условиям 
=x
=0
=x
– частное решение задачи Коши.
§18
Линейные уравнения первого порядка.
Определение:
Линейным уравнением первого порядка называется следующее дифференциальное уравнение.
коэффициенты
уравнения в общем случае функции от х
-
правая часть уравнения.
Будем
предполагать, что старший коэффициент
уравнения равен нулю 
Теорема:
Если коэффициент линейного уравнения и его правая часть непрерывны на некотором интервале оси ох, то для любых начальных условий, если только х0 берётся из этого интервала, задача Коши имеет единственное решение.
Следствие:
У линейных уравнений нет особого решения
1) Линейные однородные уравнения n-ого порядка f(х)
2
)
Линейные неоднородные уравнения n-ого
порядка f(х)
Линейные однородные дифференциальные уравнения n-ого порядка
Теорема:
Общее решение линейные однородные уравнения n-ого порядка имеет вид следующей линейной комбинации:
, где 
-
линейно независимые частных решения
линейного уравнения.
Определение:
Упорядоченная совокупность из n независимых частных решений линейного уравнения называется фундаментом системы решений.
ЛНФ - нельзя получить тождественно равным нулю из линейной комбинации не уничтожив каждую.
Определение:
Вронскианом системы функций называется следующий определитель:
W(x)=
Теорема:
Вронскианом ФСР линейные однородные уравнения n-ого порядка не при одном значении х в 0 не обращается.
Замечание:
Для произвольного линейного однородного уравнения n-ого порядка найти ФСР невозможно, хотя для каждого
линейного однородного уравнения n-ого порядка существует бесчисленное множество ФСР.
Существуют важные частные случаи, для которых ФСР находится без интегрирования - линейные однородные уравнения n-ого порядка с постоянным коэффициентом.
§19
Линейные однородные дифференциальные уравнения n-ого порядка с постоянным коэффициентом.
– Числа
Определение:
Пусть дано произвольное линейное однородное дифференциальное уравнение n-ого порядка с постоянным коэффициентом его характеристическим уравнением называется следующее алгебраическое уравнение:
степень, а не
производная
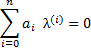
Характеристическое уравнение:
Вид ФСР напрямую зависит от корней характеристического уравнения. У любого характеристического уравнения ровно n корней.
Они могут быть:
1)Вещественными
2)Комплексными (сопряжёнными)
3
)Однократные
или кратные
не являются корнями являются корнями и
производной, но являются производной и уравнения
корнями уравнения
Основная теорема:
1)
некратные, то 
2)
кратности, то 
,
,
3)
некратные
4) Кратна пара комплексных сопряжённых корней аналогично случаю 2.
Примеры:
1)
, где {
,
}-
ФСР
Характеристическое уравнение:
=3
y=
–
общее решение
2)
,где {
,
}-
ФСР
Характеристическое уравнение:
=>
y=
-
общее решение
3)
,где { , }- ФСР
=> комплексные некратные. 
=>
y=
– общее решение
4)
,
y(0)=1, 
=>
y=
Подставим начальные условия:
=>
y=
y=
–(решение задачи Коши-единственное-оно
есть)
§20