Задача Условного Экстремума

Пусть функция z= f(M) задана в некоторой области D Eⁿ .Пусть на точку М наложены некоторые ограничения

 x_1, x₂... x_n)=0

x_1, x₂... x_n)=0 (m< n)

x_1, x₂... x_n)=0

Найти экстремум функции, но только среди тех точек, которые удовлетворяют указанным ограничениям.

Замечание:

Ограничения, наложенные на точку, называют условиями связи.

Методы решения условного экстремума.

1)Из условий связи выражают независимые переменные (m-штук) и подставляю в исходную функцию, при этом задача условного экстремума - задача обычного экстремума в пространстве меньшей размерности.

Недостаток:

Аналитически выразить переменные из условия связи невозможно.

2)Метод множителей Лагранжа.

Определение:

Пусть дана задача условного экстремума, функцией Лагранжа этой задачи называется следующая функция:

L(M, )=f(М)+ , где Λ= вектор множителей Лагранжа, пока некоторые независимые числа.

Теорема:

Если в точке М₀ функция z= f(M) имеет условный экстремум, то он совпадает с обычным экстремумом функции Лагранжа, обратное неверно.

Алгоритм решения методом множителей Лагранжа.

1)Необходимое условие условного экстремума.

, i=1…n

m-условий, m+n – уравнений

Из полученной системы определяется координаты возможных точек условного экстремума, а также соответствующие им множители Лагранжа.

2)Достаточные условия условного экстремума.

2.1) В L(M, ) подставляется вектор :L(M, ).

2.2)Дифференцируется условие связи m- дифференциалов

2 .3)Из системы дифференциалы линейно выражается дифференциалы m независимых переменных через дифференциалы оставшихся n-m.

2 .4)Берём второй дифференциал функции Лагранжа L(M, ) и в него подставляют выраженные дифференциалы из пункта 2) 3). M₀

2.5)Полученный уменьшенный второй дифференциал (M, ) исследуют на знакоопределенность обычными методами, например с помощью матрицы Гесса. M₀

Пример:

z=x₁²+x₂²

У словие связи: х₁+х₂-2=0 решить задачу условного экстремума

x_1, x₂)

Составим функцию Лагранжа.

L(x_1, x₂) имеет вид = x₁²+x₂²+ (х₁+х₂-2)

1. Необходимое условие условного экстремума

2 х₁+ =0 = -2

2х₂+ =0 => х₁=1 => M₀(1;1)стационарная точка – в ней может быть условный экстремум = -2

х₁+х₂-2=0 х₂=1

Достаточное условие экстремума

2.1) L(x_1, x₂,-2)= x₁²+x₂²- 2х₁-2х₂+4

2.2) d(х₁+х₂-2)=0

dх₁+dх₂-d(2)=0 => dх₁+dх₂=0

2.3) Выражаем один дифференциал через другой

dх₁= -dх₂

2.4)

L= +2 d x₁d x₂+ (d x₂)²

=2; =2; =0 =>

L(M₀,-2)= +2*0*d x₁d x₂+2

= +2*0*(-d x2)d x₂+2 =4

2.5)

=4 всегда > 0 => в точке M₀(1;1) условный минимум.

Г рафическая иллюстрация.

2 2

M₀(1;1) условный минимум

§12

Понятие о задаче оптимизации.

Математически простейшая задача оптимизации звучит следующим образом:

Дона некоторая функция z= f(M) в D Eⁿ . В области D задана некоторая другая область, например D₁ в общем случае с ней не совпадающая D₁ D. Найти такую точку М₀ D₁ , что f (М₀)max (или min)по сравнению с другими точками D₁

Отметим:

Функция f(M) называется целевой функцией задачи.

Область D₁ – назовём областью допустимых планов, точку М₀ называём оптимальным планом задачи.

Проблемы задачи оптимума:

1)Проблема существования

2)Проблема единственности

3)Проблема поиска

Отметим:

Решение задачи оптимума в общем случае не возможно.

Для задач из разных областей техники разработали либо какие-то частные алгоритмы позволяющие найти оптимум в частных случаях, либо численные алгоритмы, позволяющие найти оптимум численным методом.

Пример:

z=x₁²+x₂²-х₁ х₂- х₁-х₂

D ₁: х₁ ≥0 D₁ х₁Ох₂

х₂ ≥0 D₁ х₁ох₂

х₁+ х₂≤3

Решить задачу оптимизации.

1)Функция непрерывна, а область замкнута и ограничена => функция достигнет своего супремума и инфинума .

Следовательно, решение задачи оптимума в любом случае существует.

2)Сколько оптимальных точек заранее сказать нельзя.

3)Оптимальные точки могут находиться либо на границах облости, либо являться внутренними точками.

Если оптимум находится во внутренней точке, то такой точкой может быть только точка возможного экстремума.

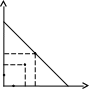
3 D₁ z=x₁²+x₂²-х₁ х₂- х₁-х₂

2х₁-х₂-1=0 2х₁-х₂=1

х₁=0 2х₂-х₁-1=0 2х₂-х₁=1

1,5 М₄

1 М₁ х₁+ х₂=3

М₃ 0,5

0,5 1 1,5 х₂=0 3

М₂

=> х₂=2 х₁-1=> - х₁+2(2 х₁-1)=1

3 х₁=3=> => М₁(1;1)

Остальные точки оптимума находятся на границе

1)х₂=0=> х₁ [0;3] =>z(х₁;0)=

=2х₁-1=0=>х₁=0,5

М₂(0,5;0)

2)х₁=0=> х₂ [0;3] =>z(х₂;0)=

=2х₂-1=0=>х₂=1/2

М₃(0;0,5)

3)х₁+х₂=3=> х₂=3- х₁=> х₁ [0;3], х₂ [0;3]

z(х₁; 3- х₁)= х₁+(3- х₁)²- х₁(3- х₁)- х₁-(3- х₁)= x₁²+(3- х₁)²+ x₁²-3 x₁-3

=4x₁+2(3- х₁)-3=2х₁-3=0=> х₁=1,5; х₂=1,5

М₄(1,5; 1,5)

Дополнительно включаем в исследование точки перелома или угловые точки М₅(0;0), М₆(3;0), М₇(0;3)

Точек возможного экстремума 7.

Мi	z(Мi)
М1(1;1)	-1
М2(0,5;0)	-0,5
М3(0;0,5)	-0,5
М4(1,5; 1,5)	-0,75
М5(0;0)	0
М6(3;0)	6
М7(0;3)	6

z min=> М₁(1;1)

z max=> М₆(3;0) и М₇(0;3)

§13