
- •Частные производные функции n-переменных.
- •Производная по направлению и градиент функции n-переменных
- •Поверхность уровня функции n-переменных.
- •Дифференцирование сложных функций.
- •Формула Тейлора
- •Экстремум функции n-переменных
- •Задача Условного Экстремума
- •Понятие о задаче оптимизации.
- •Дифференциальные уравнения.
- •1.1Основные понятия.
- •Дифференциальные уравнения первого порядка.
- •Некоторые сведения об особых решениях.
- •Уравнения второго порядка, допуск понижения.
- •Линейные уравнения первого порядка.
- •Линейные однородные дифференциальные уравнения n-ого порядка с постоянным коэффициентом.
- •Линейные неоднородные дифференциальные уравнения n-ого порядка.
- •Системы дифференциальных уравнений – несколько уравнений взятых вместе.
- •Линейные однородные системы
- •Устойчивость линейной системы. Точки покоя.
- •Кратные интегралы
- •Замена переменной в двойном интеграле
- •Поверхностные интегралы.
Некоторые сведения об особых решениях.
Если дифференциальное уравнение дано в разрешённой форме, то особыми решениями могут быть линии, на которых рвётся производная по у от правой части (f ‘y -рвётся). В общем случае особые решения могут быть огибающие общих решений:
О
 бщие
бщие
решения


 огибающая
огибающая
Огибающую можно найти из следующей системы уравнения.
Ф (х;у;с)=0
(х;у;с)=0
Ф’c(х;у;с)=0
Пример:
1 )
)![]()
![]() – рвётся при у
,
то есть на оси ох
– рвётся при у
,
то есть на оси ох
f(х;у)
![]() ;
;
![]()
![]() =x+c
=> y=(x+c)3
– семейство кубических парабол сдвинутых
по оси ох
=x+c
=> y=(x+c)3
– семейство кубических парабол сдвинутых
по оси ох
Ни при одной «с» из этого семейства ось ох: у(х) не получится.
При
этом у(х)
обращает уравнение в тождество (0)2![]() – верно => т.е. у(х)
– решение, особое.
– верно => т.е. у(х)
– решение, особое.



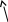
 огибающая
(особое решение) у(х)=0
огибающая
(особое решение) у(х)=0
 частное
решение y=(x+c0)3
частное
решение y=(x+c0)3
2)![]()
f(х;у)
![]() – рвётся там же при у(х)
– рвётся там же при у(х)
но у(х) – не является никаким решением уравнения.
3)![]()
Решаем уравнение:
![]()
![]()
arcsiny=x+c; y=sin(x+c) – семейство синусоид, есть ли огибающая?
y -sin(x+c)=0
-sin(x+c)=0
(y-sin(x+c))’=0 -cos(x+c)=0
y =sin(x+c)
=sin(x+c)
cos(x+c)=0
x+c=![]() =>
=>
y =1
- || ox
=1
- || ox
y= - 1- || ox => две огибающие, два решения-особых решения.
§15
Неразрешённые уравнения.
F(x,y,y’)=0 – неразрешённое уравнение
Основное отличие от разрешённых уравнений – для неразрешённых, вообще говоря, не выполняется теорема Коши.
Методов решения разрешённого уравнения нет.
Можно выделить два частных случая.
1)y=f(y’,x)
2)x= f(y’,y)
Эти уравнения иногда интегрируются с помощью замены у’=z при этом общее решение в параметрической форме.
Пример:
![]()
Замена
![]() => y=t2+xt-x
=> y=t2+xt-x
Продифференцируем полученное уравнение.
![]()
![]()
![]()
![]()

![]()
![]() ;
; ![]() -
линейное уравнение первого порядка
-
линейное уравнение первого порядка
x=UV
![]()
![]() =>
=>
![]() =>U=2(t(-
=>U=2(t(-![]() =>
=>
x=2(t(-![]()
x=2![]()
x(t)= 2
y(t)=![]() -
общее решение в параметрической форме.
-
общее решение в параметрической форме.
§16
Уравнения высших порядков.
Уравнение n-ого порядка в общем виде:
F(x,y,y’,…,y(n))=0
В разрешённой форме:
y(n)= f(x,y,y’,…, y(n-1))
Для определения n-ого порядка можно сформулировать определение общего и частного решение, начальных условий и задачу Коши.
Общее решение будет содержать n-произвольных постоянных С1, С2,…, Сn,в частном решении все произвольные постоянные станут числами.
Начальные условия имеют вид:
у(х0)=у0
у’(х0)=у’0
:
![]() =
=![]()
Аналогично первому порядку можно сформулировать задачу Коши.
Пусть
дано уравнение n-ого
порядка в разрешённой форме, если правая
часть уравнения как функция n-переменных
непрерывна в некоторой n-мерной
области D
вместе с производными ![]()
то через каждую точку М0(х0,у0)области D1 плоскости xoy , которая является проекцией области D на двумерное пространство единственное частное решение удовлетворяющее начальным условием задачи Коши.
Как и для случая первого порядка методик нахождения общего решения не существует.
В некоторых случаях удаётся искусственным путём понизить порядок уравнения или решить специальными методиками.
Два основных типа n-ого порядка.
§17
