
№146.11.Барщевский
.pdf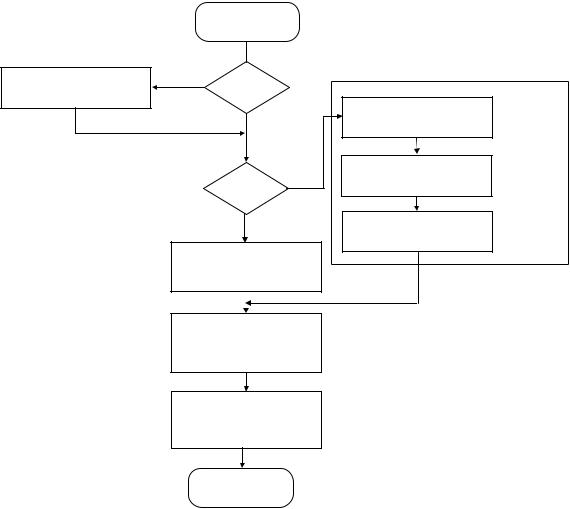
Изменение структурных связей
171
|
Начало |
Нет |
А = ? |
|
|
|
Да |
Б = ? Нет
Да
Ресурсное обеспечение плана
Решение для элементов
(уровни h= 1 - 3)
Согласование интересов элементов и уровней
Конец
Решение Классификация по частям
Ресурсное обеспечение плана
Решение для компонент
Рис. 9.5. Последовательность процесса планирования:
А – параметры среды неизменны; Б – решение целиком
Необходимо, следовательно, определить условия, гарантирующие совместность. Здесь возможно несколько случаев:
1)определение плана Р’[T] < Р[T] < R-[T], который может быть выполнен при имеющихся ресурсах;
2)определение минимального дополнительного количества ресурсов b(Tr), позволяющих выполнить заказ R-[Tp];
3)сочетание случаев 1 и 2.
Для определения условий совместности, как показано в [2], возможно использовать методы квазиобратных матриц, прямое вычисление, метод невязок,
втом числе многокритериальную оптимизацию. Два первых метода проще в решении, однако они определяют лишь границу совместности, не учитывая стоимостных характеристик.
Всвязи с этим предпочтителен последний метод. При его использовании
вобщем виде необходимо решать дополнительную задачу
172
P[Tp] + R-[Tp] ≥ R-[Tp],
AP[Tp] ≤ b(Tr) + b(Tr), |
(9.21) |
F = <C, R-[Tp]> + <D, b(Tr)> Æ min,
где C и D – стоимостные веса. или веса, приводящие разноразмерные величины к одной размерности.
Чаще всего используется вариант R-[Tp] = 0 и b(Tr) ≠ 0, о котором далее пойдет речь.
Вопросы ресурсного обеспечения тесно связаны с постоптимальным анализом чувствительности решений:
Определяется область [bψmin*(Tr), bψmax*(Tr)] инвариантности решения P[Tp], т.е. границы изменения вектора bψ*(Tr), в рамках которых вектор решения не изменяется. Определяется “грубость” решения и осуществляется более рациональный выбор значения вектора b*(Tr).
Совместность задачи (9.10) в целом может быть проверена и с использованием декомпозиции.
После определения (одним из рассмотренных способов) величины b*(Tr) возможно решение задачи (9.10) “целиком” любым из известных (в том числе последовательных [2]) методов.
Векторный критерий. Для оптимального планирования с одной целевой функцией (скалярным критерием) характерны следующие обстоятельства:
1)выбор вида целевой функции – процедура неформальная и неодно-
значная;
2)вид целевой функции оказывает существенное влияние на характер функционирования системы;
3)использование только одного критерия характеризуется получением «крайних» решений, не учитывающих в достаточной мере факторов, имеющих место в реальной системе.
Для «сглаживания» этих крайностей используется векторная целевая функция (многокритериальная постановка задачи).
В качестве элементов векторных целевых функций могут быть использованы критерии, указанные в [2].
Составляющими критерия могут быть выпуск товарной продукции; производительность труда; рентабельность; фондоотдача; удельные затраты на выпуск продукции; объем и стоимость незавершенного производства; себестоимость. В качестве составляющих векторного критерия выбраны и прибыль; доход; объем товарной продукции в оптовых ценах; нормативно-чистая продукция. Независимо от выбора критериев формально в линейном варианте они различаются коэффициентами (весами) αl при целевых функциях.
173
Нахождение решений при векторной целевой функции математически существенно усложняется и связывается с определением равновесия по Парето
[2].
Полученные ранее оптимальные значения планов Р*[Tp], P*k[ti] вычислены для скалярных целевых функций. Не снижая общности, считаем их первыми (l = 1, lk = 1) в векторных целевых функциях (9.10) и (9.12), (9.19) и обо-
значим через Р1*[Tp], P*1k[ti] (или Р1k*[Tp]).
Аналогично решаются задачи для критериев Fl(Р*[Tp]) и Fl(P*k[ti]) для l = 2, L и lk = 2, Lk соответственно и получаются значения Рl*[Tp], P*lk[ti]. Результаты решения векторной задачи в значительной мере определяются самой неформальной постановкой (схемой компромисса) задачи – переходом от векторного критерия к скалярному.
Учет L критериев возможен двумя основными группами способов, сводящимися в конечном итоге к сворачиванию векторного критерия Fl к скалярному F через веса αl:
L L
F(Р*[Tp]) = Σ αl Fl(Р*[Tp]) Æ max, Σ αl = 1, αl ≥ 0: (9.22) |
|
l =1 |
l =1 |
1)веса критериев заданы (назначены) априорно (экспертами);
2)веса определяются в процессе решения задачи.
Как показал анализ [2], предпочтение следует отдать второй группе методов, при использовании которой возможно использование следующих методов:
а) метод минимальных потерь от всех критериев (метод С2); б) метод идеальной точки (метод СЗ).
Для их формального представления введем (при Flmin = 0) обозначение
gl(Р[Tp]) = 1 + dl(Р[Tp]),
dl(Р[Tp]) = - Fl(Р*[Tp])/ Flmax,
где Flmax, Flmin – максимальное и минимальное значение целевых функций. Очевидно, что gl Æ min соответствует Fl Æ max.
В методе С2 задача векторной оптимизации приводится к виду
AP[Tp] ≤ b(Tr),
zl’ ≥ gl (Р[Tp]), (9.23)
zl’ Æ min.
В методе СЗ первоначально определяются оптимальные значения Р*l[Tp] и Flmax для отдельных l-х критериев, а затем решается задача
AP[Tp] ≤ b(Tr),
174
L
F(Р[Tp]) = Σ {Flmax - Fl (Р[Tp])}2 Æ min.
l =1
Окончательный выбор применяемого метода векторной оптимизации определяется исследователем (ЛПР). Для работы ЛПР с позиций простоты алгоритма и времени его реализации можно дать следующие качественные рекомендации:
1)метод СЗ наиболее подходит по физическому смыслу, хотя и требует квадратичного программирования;
2)при дробно-линейных целевых функциях [2] метод С2 также трансформируется в задачу квадратичного программирования.
Поскольку векторный критерий может быть приведен к виду (9.22), далее оперируем с описанием вида (9.9).
Введем допущение, что целевые функции элементов и уровней согласо-
ваны.
Ограничения снимаются в данной главе позднее.
Использование декомпозиции. До сих пор считалось, что размерность задач позволяла решать их целиком.
При большой размерности векторов Р и Pk решения находятся с использованием декомпозиции (рис. 9.5) с постепенным укрупнением структуры по схеме “компонента – элемент – уровень – система”, где под компонентами понимаются составные части, на которые разделяется элемент структуры.
Будем далее рассматривать задачу (9.10) без второго выражения, полагая, что оно соответствующим образом введено в первое. Считаем, что задачи ресурсного обеспечения и векторного характера критерия рассмотрены.
Декомпозиция подразумевает:
1)выделение сильно связных множеств (классификация);
2)декомпозиционное решение задачи.
При выполнении процедуры классификации полезно учитывать следующие предварительные рекомендации:
1)выбирать количество классов К в пределах 6–8 с одинаковым по возможности числом элементов m в каждом;
2)иметь между классами минимум связей, чтобы уменьшить информационный обмен и значительно увеличить скорость решения;
3)использовать для классификации предпочтительно простые, быстродействующие и эффективные алгоритмы.
Данная задача является нестандартной задачей кластеризации, ибо проводится на двудольном графе.
Ее трудно представить формально в виде задачи целочисленного программирования, что служит одной из причин применения для решения таких задач эвристических алгоритмов [2].
175
Предлагается использовать известный алгоритм 4.1 приложения 4.
Для декомпозиции возможно использование алгоритмов выделения сильно связных множеств [2].
Задача содержательно ставится так. Необходимо разделить N элементов, связи которых характеризуются коэффициентами матрицы А = {aqv}, на K классов по mk (k = 1, K) элементов в каждом так, чтобы взвешенная сумма связей между классами была минимальна.
Рассмотрим случай, когда заданы количество классов K и число элементов в классе mk (часто mk = m = const).
Используемые методы возможно разделить на точные и приближенные. Точная постановка данной задачи имеет вид алгоритма 4.2 приложения 4. Это задача целочисленного квадратичного программирования” обладающая большим количеством переменных l = КN + KN2 и значительным числом ограничений m = KN2 + K. Уже при K = 2 и N = 6 размерность задачи l × m =
84 × 74.
Задача (П.1)–(П.5), как показано в [2], может быть приведена к задаче линейной целочисленной:
K |
N |
N |
F = Σ |
Σ |
Σ aqv yqvk Æ max |
k = 1 q = 1 v = 1
N N
Σ Σ yqvk = m2, (9.24)
q = 1 v = 1
K N
Σ Σ yqvk = m,
k = 1 v = 1
K N
Σ Σ yqvk = m,
k = 1 q = 1
где yqvk = {0, 1}, mk = m.
Задача имеет размерность l × m = KN2 × (K + 2N) и уже для К = 2 и N = 6 размерность l × m = 72 × 14. Следовательно, и такая задача при значительных величинах K и N характеризуется высокой размерностью (и длительным временем решения).
В связи с этим предпочтительнее приближенные методы:
1)метод эквивалентных преобразований;
2)последовательные методы.
Из двух разновидностей метода эквивалентных преобразований [2] более универсальным и конструктивным является метод, составленный из двух процедур: нахождение первого приближения; улучшение решения путем целенаправленной перестановки строк и столбцов матрицы А.
176
В процедуре нахождения первого приближения задача (П.1)–(П.5) приложения заменяется на линейную задачу целочисленного программирования. Ее применение описано в [2]. Процедура улучшения решений в общем случае может не привести к оптимальному решению.
Процедуры метода эквивалентных преобразований при большой размерности матрицы А являются задачами достаточно сложными и самостоятельными.
Желание упростить и совместить эти процедуры привело к широкому использованию последовательных методов.
Их идея заключается в последовательном выделении k-го семейства (класса) и исключения его элементов (и связей) из матрицы А на последующих итерациях. «Центром», вокруг которого образуется каждый k-ый класс, служит опорный элемент, выделяемый по критерию
N
F = Σ aqv Æ max. (9.25)
v = 1
На базе последовательных методов автором сформулирован [2] и предлагается алгоритм, отличительной чертой которого является рассмотрение на каждой итерации только двух классов (алгоритм 6.3).
Отметим также, что структура матрицы А задачи (9.10) с выделенными подматрицами - кластерами может быть двух видов:
A = {Aij}, i, j = 1, Ω, (9.26)
где диагональные элементы обозначаются как Ai характеризуют выделенные классы, а матрицы Aij определяют связи между классами, или
A1 |
A2 |
A3….. AΩ |
|
A1 |
0 |
0……..0 |
|
A = 0 |
A2 |
0……..0 |
(9.27) |
……………………. |
|
||
0 |
0 |
0…….A1Ω |
|
при использовании более прогрессивного лимитного метода декомпозиции. Сказанное относится и к матрицам Аk выражений (9.12).
Нетрудно видеть, что структура (9.27), являясь частным случаем (9.26), не всегда может быть получена.
В связи с этим основные методы классификации обсуждаются для струк-
туры (9.26).
Сравнительный анализ методов кластеризации позволяет рекомендовать последовательные методы (алгоритмы А1, А4).
После выделения Ω классов в структуре матрицы А задачу (9.10) можно переписать в виде:
177
АωPω[Tp] ≤ bω(Tr), ω = 1, Ω (9.28)
Ω |
(9.29) |
Σ АωPω[Tp] ≤ b0(Tr), |
|
ω = 1 |
|
Ω |
Æ max, (9.30) |
Fl(Pω[Tp]) = Σ <Clω, Pω[Tp]> |
|
ω = 1 |
|
где b(Tr) = {b0T(Tr), bωT(Tr), ω = 1, Ω}T; bω(Tr), b0(Tr), - вектор-столбцы локаль-
ных и общих (глобальных) ресурсов системы; P[Tp] = {PωT[Tp]}T, Cl = {Clω, ω = 1, Ω}.
Аналогичные преобразования могут быть сделаны для выражений (9.12), (9.14), (9.16)–(9.20).
Если каким-либо образом удается (лимитный метод) представить (9.29) в
виде
Ω
b0(Tr) = Σ b0ϖ(Tr),
ω = 1
то задача (9.28)–(9.30) декомпозируется на Ω прямых локальных задач АωPω[Tp] ≤ b0ϖ(Tr)
АωPω[Tp] ≤ bω(Tr),
Ω
Fl(Pω[Tp]) = Σ <Clω, Pω[Tp]> Æ max (9.31)
ω = 1
и одну глобальную задачу
Ω
Σ b0ϖ(s – 1)(Tr) ≤ b0(Tr),
ω = 1
Ω
F{b0(Tr)} = Σ w0ωsT[Tp] b0ω(s - 1)(Tr) Æ max, (9.32)
ω = 1
где s (s = 1, S) – номер итерации; w0ω – двойственная переменная; «т» – символ транспонирования.
При декомпозиционном подходе необходима проверка совместности задач (9.28)–(9.30) и (9.31). Условия совместности ω-задачи (9.28)–(9.30) и задачи (9.31) трансформируются с заменой [2] b0ω на (b0ω + b0ω), bω на (bω + bω) с ценами D0ω и Dω соответственно.
Потребное количество ресурсов для решения задач определяется выраже-
ниями b0ω* ≥ b0ω + b0ω), b*ω ≥ (bω + bω).
При декомпозиционном решении задачи (9.10), равно как и (9.12), (9.19), имеет место сходящийся итерационный алгоритм 4.3 приложения 4.
178
Таким образом, определен оптимальный план Р*[Тp] для задачи (9.10) при ее решении целиком (ω = 1) или через ω-компоненты при декомпозиционном решении [2].
Аналогично получаются решения Рk[ti] для отдельных k-ых (k = fixe, k = 1, K) элементов, описываемых выражениями (9.12), (9.19).
Отметим, что «факторизованная» задача при декомпозиционном способе дает то же решение, которое получается при рассмотрении задачи целиком.
9.3. Согласование интересов элементов процесса планирования
Снимем допущение (целевые функции элементов и уровней согласованы) параграфа 9.2 и рассмотрим более подробно процесс согласования работы (координации целевых функций и ограничений) элементов и уровней.
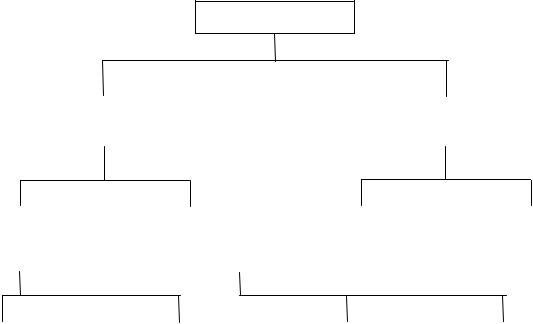
В задаче согласования интересов в принятой трехуровневой системе могут быть выделены два класса задач (рис. 9.6).
Согласование
Горизонтальное, h=2 |
|
Вертикальное |
|
|
|
Локальные усло- |
|
Локальные усло- |
|
h=1, h=2 |
|
h=2, h=3 |
вия не соблюда- |
|
вия соблюдаются |
|
|
|
|
ются |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Равновесие по |
|
|
|
Определение новых |
|
Нет новых ресур- |
|
Векторная опти- |
|
|
|||
Нэшу |
|
мизация |
|
ресурсов |
|
сов |
|
|
|
|
|
|
|
Рис. 9.6. Согласование интересов
1.Горизонтальное согласование (элементов k = 1, К на уровне h = 2).
2.Вертикальное согласование:
а) элементов k = 1, К уровня h = 1 с элементами уровня h = 2; б) элементов уровней h = 2 и h = 3.
Для решения перечисленных классов задач представим описание (9.12)– (9.13), (9.16)–(9.19) уровня h = 2 в несколько иной форме
179
K
Fl(Рk[Tp]) = Σ Flk (Рk[Tp]) Æ max
k =1
A2kPk[Tp] ≤ b2k(Tr), k = 1, K, (9.33)
A1kPk[Tp] ≤ Pk – 1[Tp], k = 2, K, (9.34)
Pk - 1[Tp] ≥ P’k – 1[Tp],
PK[Tp] ≥ R-[Tp], k = K, (9.35)
A11P1[Tp] ≤ b(Tr), k = 1, (9.36)
где P’k – 1 – минимально необходимое количество материальных ресурсов на входе k-го элемента; b2k – количество нематериальных (ненакапливаемых) ресурсов; A1k, A2k – матрицы удельных расходов накапливаемых (материальных)
и ненакапливаемых ресурсов: PkI[Tp], PIIk[Tp], – решения, полученные на уров-
нях h = 1 и h = 2; Ak = (A1k, A2k)T.
Выражения (9.34) характеризуют горизонтальные (класс 1) связи, а выражения (9.35), (9.36) – вертикальные (классы 2а и 2б) связи. Ограничения в выражении (9.33) будем называть локальными.
Отметим, что при определении Pk[ti] вместо Pk[Tp] размерность задачи существенно увеличится. Однако р-интервальную задачу можно по-прежнему решать как (р – 1) двухинтервальных задач.
Для решения задачи класса 1 используем выражения (9.12), (9.19), (9.33)– (9.36). Не снижая общности, можно положить, что целевые функции k-ых элементов – векторные.
В задаче класса 1 рассмотрим два случая:
1) локальные ограничения (9.33) не влияют на решения т.е. всегда соблюдаются условия
A2kPk[Tp] ≤ b2k(Tr), k = 1, K; (9.37)
2) условия (9.37) не соблюдаются.
В первом случае ограничениями (9.37) можно пренебречь. Для этого случая предлагается алгоритм 4.4 приложения 4.
Возможно использовать теорию игр – равновесие по Нэшу (алгоритм 4.5 приложения 4) и методы решения задач с векторным критерием.
При использовании теории игр можно, не снижая общности, считать, что для элементов k = 1, n величины Fk < 0, а для элементов k = n +1, K (n, n + 1 1, K) – величины Fk > 0.
Очевидно, что при плане Р2k[Tp] потери несут элементы k = n + 1, K и система в целом, при плане Р1k[Tp] потери характерны для элементов k = 1, n. Тогда в интересах системы в целом целесообразно дополнительный выигрыш

180
K
Σ Fr
r = n + 1
при плане Р1k[Tp] перераспределить с учетом элементов k = 1, n по правилу
K |
K |
δFk = (Σ | |
Fr| | Fk|)/Σ | Fk,|, (9.37, а) |
r = n + 1 |
k = 1 |
Можно показать, что решение (9.37, а) существует. Тогда компромиссным (равновесным) решением будет Р’k[Tp], а значения целевых функций
Fk(Р1k[Tp]) + δFk, k = 1, n,
Fk(Р’k[Tp]) = |
(9.37, б) |
|
Fk(Р1k[Tp]) - δFk, k = n + 1, K. |
Устойчивость равновесия по Нэшу показана в алгоритме 4.6 приложе-
ния 4.
Недостатки использования равновесия по Нэшу – итеративный характер решения и потребность для k-го элемента информации о всех других элементах (что практически исключено и избыточно).
Эти недостатки не имеют места при использовании предложенных автором [2] методов решения векторных задач. Введем обозначения
Fkmin = |
Fk(Р1k[Tp]), k = 1, n |
(9.38) |
|
|
Fk(Р2k[Tp]), k = n + 1, K |
Fkmax = |
Fk(Р2k[Tp]), k = 1, n |
(9.39) |
|
|
Fk(Р1k[Tp]), k = n + 1, K, |
gk = {Fkmax - Fk(Р’k[Tp])}/{Fkmax - Fkmin}, (9.40)
где Р’k[Tp] – компромиссное решение.
Тогда для решения задачи согласования возможно использовать методы С2–СЗ векторной оптимизации.
При использовании метода идеальной точки (СЗ) целевые функции могут иметь вид
n K
F’ =Σ{Fk(Р2k[Tp]) – Fk(Р’k[Tp])}2 + Σ {Fk(Р1k[Tp]) – Fk(Р’k[Tp])}2 Æ min, (9.41) |
|
k = 1 |
k = n + 1 |
или
n K
F’ = Σ{Р2k[Tp] – Р’k[Tp]}2 + Σ {Р1k[Tp] – Р’k[Tp]}2 Æ min. |
|
k = 1 |
k = n + 1 |
