1.8. Геометрические вероятности

Область применения классического определения вероятности ограничена испытаниями с конечным числом равновозможных исходов. К описанию ситуации с бесконечным числом “равновероятных” исходов приспособлено геометрическое определение вероятности. При этом определять вероятности будем с помощью отношения длин, площадей и т.д.

П

Рис. 1.3.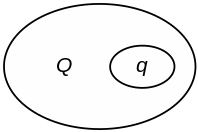

усть имеется область Q, в которой содержится область q (рис. 1.3). Тогда, если в область Q наугад брошена точка и равновозможно ее попадание в любую часть области Q, то вероятность

Р(попасть в область q) = ,

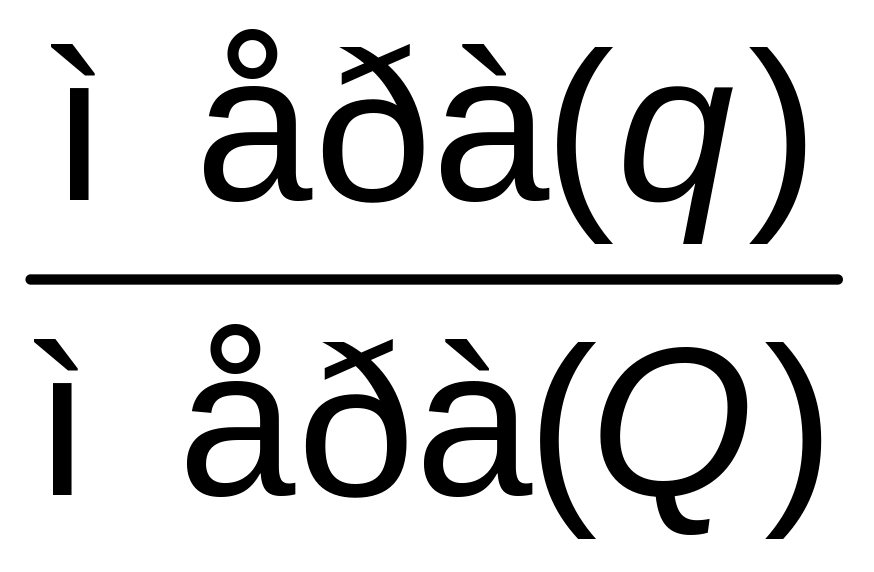где «мера» означает длину, площадь, время, объем и т.д. в зависимости от характера области.

Пример 1.8.

На светофоре зеленый и красный свет горит по 30 секунд, а желтый 10 секунд. Автомобиль подъезжает к перекрестку в произвольный момент времени. Какова вероятность того, что он проедет перекресток без остановки?

Решение

Прибытие автомобиля на перекресток можно моделировать как бросание точки в отрезок оси времени длиной в 80 сек:

,

причем, попадание в любую его часть равновозможно. Поэтому интересующая нас вероятность равна:

.

Пример 1.9.

Из интервала [0;2] наугад выбираются 2 числа. Найти вероятность того, что сумма этих чисел не менее двух, а произведение не более двух.

Решение

Обозначим числа переменными х и у, тогда возможные пары (х;у) будут принадлежать квадрату со стороной 2 (рис. 1.4). По условию и . Эти неравенства определяют некоторую область внутри квадрата, причем границы области заданы уравнениями: у=2-х, 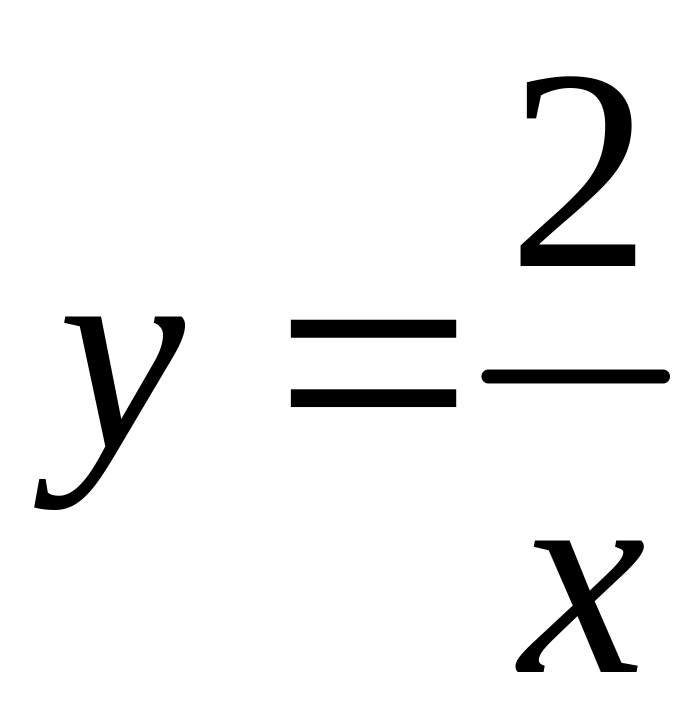. Заштрихованная область удовлетворяет системе неравенств, и искомая вероятность равна: . S_кв=4,

;

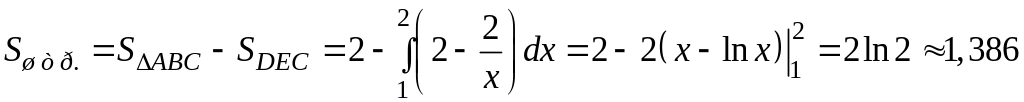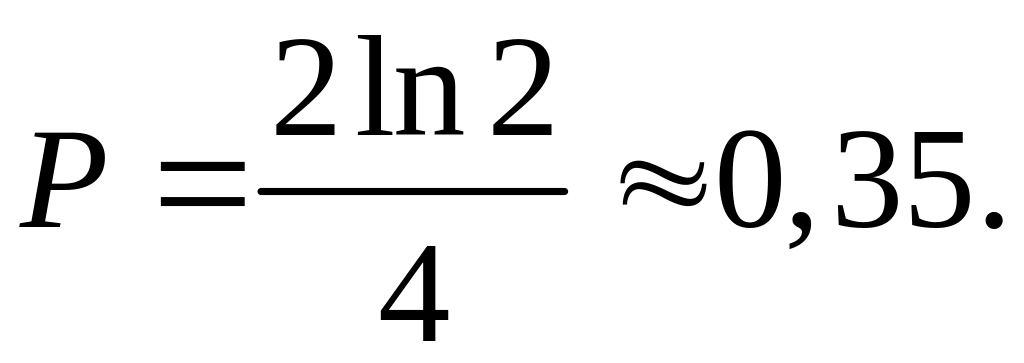
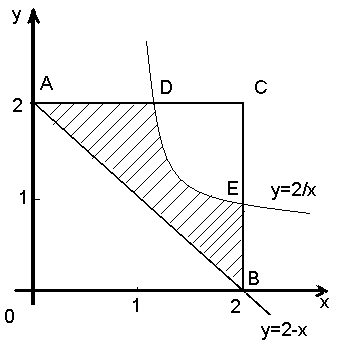
Рис. 1.4.

1.9. Теорема умножения вероятностей. Условная вероятность

При фиксированном комплексе условий каждое событие А имеет определенную вероятность. Может случиться так, что, помимо комплекса условий, известно, что произошло некоторое событие В. Как эта информация изменяет вероятность события А?

Определение. События А и В называются независимыми, если появление одного из них не меняет вероятности появления другого.

Определение. Вероятность события А, вычисленная при условии, что событие В произошло, называется условной вероятностью события А и обозначается Р (А).

Например. В семье двое детей. Согласно генетическим законам вероятность рождения мальчика и девочки примерно одинакова и равна 1/2. Возможны следующие равновозможные комбинации: ММ, МД, ДМ, ДД. Первая буква означает пол старшего ребенка. Рассмотрим события : А – в семье есть мальчик, В – в семье есть девочка, С – старший ребенок девочка. Вычислим некоторые вероятности. Р(А) = 3/4 – это безусловная вероятность и находится она по классической формуле. Вероятность того, что один ребенок мальчик, при условии, что другой – девочка, равна: (А), так как возможны три комбинации МД, ДМ, ДД, а благоприятствует только первые две из них. Р_С (А) = 1/2, так как возможны две комбинации ДМ, ДД, а благоприятствует одна из них.

В

Рис. 1.5.

общем случае задача нахождения условных вероятностей решается просто. Рассмотрим, например, случай геометрических вероятностей, для которых Р(А) равна площади области А, если площадь всего прямоугольника равна единице (рис. 1.5).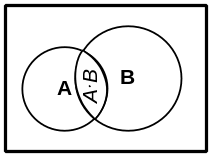

Найдем Р (А) – вероятность попасть в область А при дополнительном условии, что уже известно, что мы попали в область В. Эта вероятность будет пропорциональна отношению площади АВ к площади области В:

.

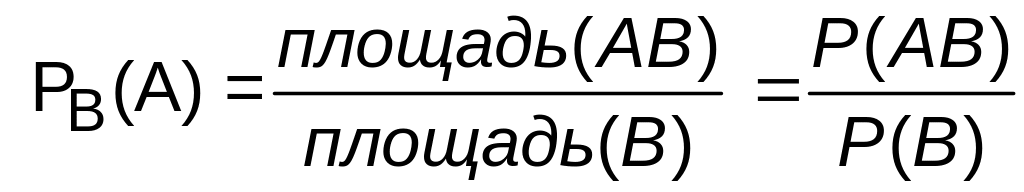Это означает, что вероятность события А вычисляется не по совокупности всех возможных исходов, а лишь по совокупности тех из них, в которых наступило событие В. Аналогично найдем Р_А (В) = .

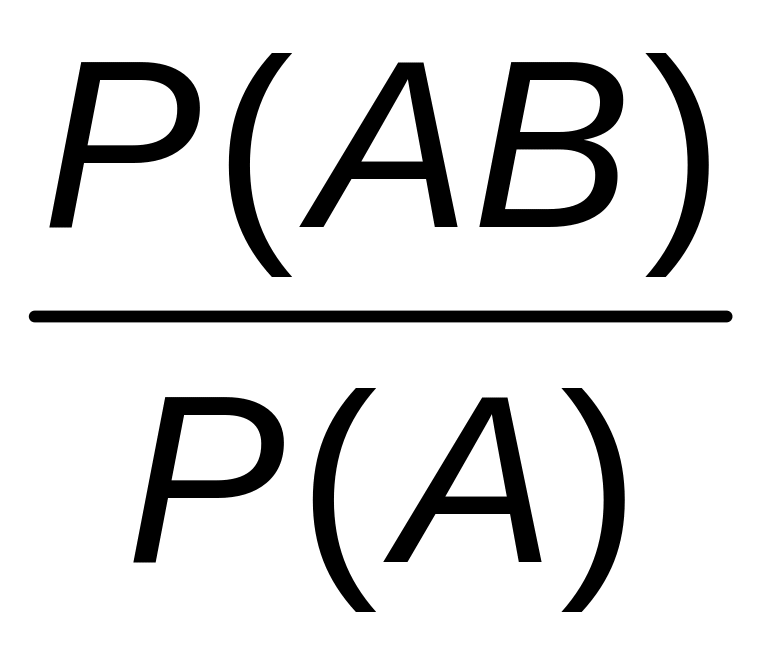Теорема 1.1. Вероятность произведения двух событий равна произведению вероятности одного из этих событий на условную вероятность другого, вычисленную при условии, что первое событие произошло.

Доказательство. Для доказательства указанного утверждения объединим полученные выше равенства и выразим из них Р(АВ):

Р(АВ) = Р(А) Р , (1.1)

если события А и В зависимые.

Если события А и В независимы, то Р и тогда вероятность произведения двух событий равна произведению вероятностей этих событий:

Р(АВ) = Р(А) Р(В), (1.2)

Замечание. Необходимо различать вероятностную и причинную зависимость. Причинная зависимость предполагает наличие направленной цепи событий: причина  следствие. Для вероятностной связи причина и следствие равноправны. События рассматриваются как результат некоторого опыта, не различая события, происходящего раньше и происходящего позже, а учитывая лишь то, как появление одного меняет вероятность появления другого.

Теорема умножения может быть сформулирована для любого числа событий.

Теорема 1.2. Вероятность произведения нескольких зависимых событий равна произведению вероятностей этих событий, причем вероятность каждого следующего по порядку события вычисляется при условии, что предыдущие имели место:

Р( = . (1.3)

Если события независимы, то

. (1.4)

Итак, прежде чем вычислять вероятность произведения совместных событий, следует выяснить зависимы они или нет.

Пример 1.10.

Имеется система четырех последовательно соединенных между собой элементов (электрическая цепь, поточная линия и т.п.). Вероятность безотказной работы (надежность) каждого элемента равна 0,9. Элементы выходят из строя независимо друг от друга. Какова надежность системы?

Решение

Пусть событие А состоит в безотказной работе (надежность) системы, а событие  – в безотказной работе i-го элемента. Для того, чтобы произошло событие А, необходимо, чтобы произошло событие и событие и событие и событие , т.е. . А так как события независимы, то применяя формулу (1.4), получим

= (0,9)⁴ 0,65.

Полученный результат означает, что последовательное соединение элементов уменьшает надежность системы.

Пример 1.11.

Проверяется партия из 20 деталей, среди которых имеется 4 бракованных. Причем изделия берутся по одному наугад и проверяются до появления первого бракованного. Какова вероятность, что бракованное изделие обнаружится на третий раз?

Решение

Введем событие А – бракованное изделие появится в третьем испытании, а событие А_i – при i-м испытании появится годное изделие. Тогда , причем события А₁, А₂, зависимы, так как выбор годного изделия уменьшает шанс выбрать годное изделие в следующем испытании. Применив формулу (1.3) имеем

.