1.6. Классическое определение вероятности

Существует класс опытов, в которых вероятность события можно вычислить, исходя из условий только самого этого опыта.

Пусть проводится эксперимент (опыт), который имеет n различных элементарных исходов, то есть при каждом испытании обязательно один из этих возможных исходов реализуется. Совокупность всех возможных исходов испытания называется пространством элементарных исходов. Те элементарные исходы, в которых интересующее нас событие наступает, называются благоприятствующими исходами этому событию.

Например, при подбрасывании игральной кости (кубика) один раз имеем шесть исключающих друг друга исходов: выпадение 1, 2, 3, 4, 5, 6 очков. Это и есть пространство элементарных исходов. Событие А –“выпадение четной цифры” имеет три благоприятствующих исхода: 2, 4, 6 очков.

Классическим определением вероятности можно воспользоваться, если число возможных исходов испытания конечно, все элементарные исходы равновозможны, несовместны и образуют полную группу.

Определение. Вероятностью события А называется отношение числа исходов, благоприятствующих событию А, к общему числу всех возможных исходов:

,

где m – число исходов, благоприятствующих событию А, n – число всех возможных исходов испытания.

В приведенном примере с подбрасыванием игральной кости Р(А) = 3/6 = = 1/2.

Классическое определение вероятности служит хорошей математической моделью тех случайных явлений, для которых важнейшим условием применения является предположение о равновозможности исходов опыта. Такие требования естественны в области азартных игр, лотерей, в организации выборочного контроля и выборочных статистических исследований. Исторически первые применения вероятностных методов относятся к XVII веку, когда разрабатывалась теория азартных игр с целью дать рекомендации игрокам. Затем эти методы стали применяться в практике страховых компаний для установления разумных страховых премий. В настоящее время практически нет области знаний, где не могли бы применяться эти методы исследования.

Подсчет числа исходов в классических случаях часто сводится к задачам комбинаторики (подразд. 1.1).

1.7. Свойства вероятностей

Из определения вероятности вытекают следующие ее свойства.

1. Вероятность любого события есть число, заключенное между нулем и единицей:

0  Р(А)  1.

Действительно, если событию А благоприятствует m исходов из возможных n исходов, то 0 m n, откуда 0 .

Вероятность достоверного события А равна единице, так как все исходы благоприятствуют событию (m=n) и Р(А) = n/n=1. Вероятность невозможного события А равна нулю, так как этому событию не благоприятствует ни один исход и Р(А) = 0/n =0 . Вероятность любого случайного события А есть положительное число, заключенное между нулем и единицей: 0 < Р(А) < 1.

2. Если А и В несовместные события, то

Р(А+В) = Р(А) + Р(В).

Пусть эксперимент имеет n равновозможных исходов, из которых исходов благоприятствуют событию А, а исходов – событию В. Так как события А и В несовместимы, то среди исходов нет благоприятствующих и тому и другому одновременно. Поэтому событию А + В благоприятствует m₁+ m₂ исходов. Следовательно,

Р(А+ В) = Р(А) + Р(В).

3. Вероятность события , противоположного событию А, равна:

Р( ) = 1 – Р (А).

В самом деле, при каждом осуществлении комплекса условий обязательно произойдет одно из событий А или , т.е. А + = (достоверное).

Cледовательно, Р (А + ) = 1, а так как события А и несовместны, то по свойству 2 имеем Р (А) + Р ( ) = 1.

Рассмотрим несколько примеров.

Пример 1.5.

В семь дней недели независимо друг от друга происходит семь событий (скажем, автомобильные аварии). Какова вероятность, что каждый день будет происходить по одному событию?

Решение

Для удобства рассуждений описанную ситуацию формализуем и представим следующим образом. Имеем семь ящиков и семь различных шаров. Тогда распределение событий по дням недели равносильно раскладке шаров по ящикам. (Подобная модель с шарами часто используется в задачах). Первый шар можно положить в любой из семи ящиков, второй – также в любой из семи и т.д., поэтому всех возможных способов раскладки шаров по ящикам будет 7⁷. Для получения числа благоприятствующих исходов разложим по одному шару в каждый ящик, а затем будем менять местами шары. Тогда число благоприятствующих случаев будет равно числу перестановок, т.е. 7!. Все элементарные исходы опыта равновозможны и, следовательно, можно воспользоваться классической формулой. В итоге имеем

Р = 0,0062.

Оказалось, что маловероятно равномерное распределение событий во времени, что согласуется с обыденным представлением о «полосе везения» и «полосе невезения» и т. п. ситуациях.

Пример 1.6.

Из M деталей N бракованных. Наугад выбирается n деталей. Какова вероятность, что среди выбранных будет m бракованных?

Решение

Так как нас интересует только состав выбора (порядок неважен), то возможных способов выбора будет . Интересующее нас событие произойдет, если m деталей будет выбрано из числа М бракованных, это можно сделать способами, и для каждого набора из m бракованных деталей будет выбрано n-m годных деталей из N-M, что можно сделать способами. Согласно комбинаторному принципу всего способов, благоприятствующих событию, будет . Искомая вероятность равна их отношению

.

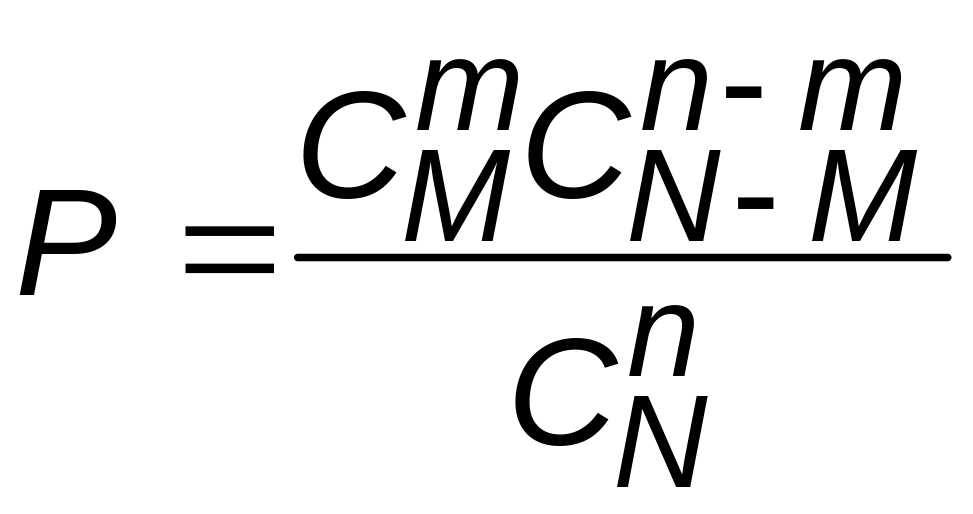Пример 1.7.

Из N билетов студент не выучил M билетов. Когда больше вероятность выбрать невыученный билет: когда тянешь билет первым или последним?

Решение

Рассмотрим событие «студент выбирает билет r-м по счету». При подсчете общего числа возможных способов выбора первых r билетов важно, какие билеты были выбраны (важен состав) и в каком порядке они выбраны, т.е. число размещений из N по r: . «Благоприятствуют» выбору невыученного билета те способы, в которых r-й билет выбран из числа невыученных М билетов и для каждого из этих М билетов предыдущие с учетом состава и порядка могут быть выбраны способами. Согласно комбинаторному принципу, всего благоприятствующих способов будет M. Тогда вероятность вытянуть невыученный билет равна:

.

Результат малоутешительный для нерадивых студентов так как не зависит от того, когда студент тянет билет: первым или последним.