6.6. Числовые характеристики системы двух случайных величин
Числовые характеристики системы случайных величин (X,Y) состоят из числовых характеристик каждой из величин, входящих в систему, и числовых характеристик, дающих представление о характере связи между величинами. Числовые характеристики каждой из величин по отдельности определяются как числовые характеристики обычных случайных величин Х и Y. Из числовых характеристик зависимости между величинами назовем лишь наиболее употребляемые.
6.6.1. Ковариация двух случайных величин
Корреляционным моментом или ковариацией случайных величин Х и Y называется математическое ожидание произведения соответствующих центрированных величин
cov (X, Y)
=
=
М((Х-М(Х)(Y-M(Y)).
Если случайные величины независимы, то их ковариация равна нулю. Обратное утверждение верно не всегда. Равенство нулю ковариации независимых случайных величин следует из теоремы о математическом ожидании произведения независимых случайных величин:
cov (X,Y)=
=
0 0 = 0.
Ковариация двух случайных величин характеризует не только степень зависимости случайных величин, но и их рассеивание вокруг точки (M(X); M(Y)).
Ковариацию часто удобно выражать через
начальные моменты случайных величин:
Таким образом, ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение математических ожиданий.
6.6.2 Коэффициент корреляции
Размерность ковариации cov(X, Y) равна произведению размерностей случайных величин Х и Y. Безразмерной характеристикой зависимости Х и Y является коэффициент корреляции
.
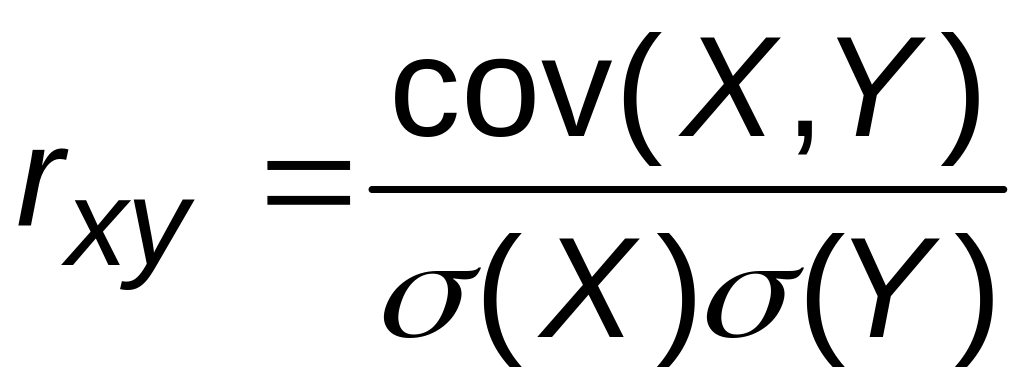Коэффициент корреляции случайных
величин Х и Y
характеризует силу зависимости этих
величин, причем только линейную
зависимость. Если
,
то случайные величины Х и Y
связаны положительной корреляцией и
при возрастании одной из них другая
также возрастает. Если
,
то корреляция отрицательна и с ростом
одной величины другая убывает. Можно
доказать, что для любых двух случайных
величин Х, Y
.
Если линейной зависимости нет, то
.
Если между Х и Y
существует функциональная линейная
зависимость
,
то
при
и
при
.
Заметим, что
означает только отсутствие линейной
зависимости между случайными величинами;
любой другой вид связи может при этом
присутствовать.
Пример 6.5.
Закон распределения системы двух
дискретных случайных величин (Х, Y)
задан таблицей. Найти ковариацию
системы и коэффициент корреляции
.
Сделать вывод о тесноте зависимости между случайными величинами Х и Y.
Х У |
1 |
2 |
4 |
0 |
0,1 |
0 |
0,1 |
2 |
0 |
0,3 |
0,3 |
5 |
0,2 |
0 |
0 |
Решение.
Ковариация вычисляется по формуле
.
Прежде всего найдем законы распределения
для Х и Y (п.
6.3).
Суммируя вероятности , стоящие в первом, затем во втором и третьем столбцах таблицы, получим:
.
Ряд распределения для Х имеет вид
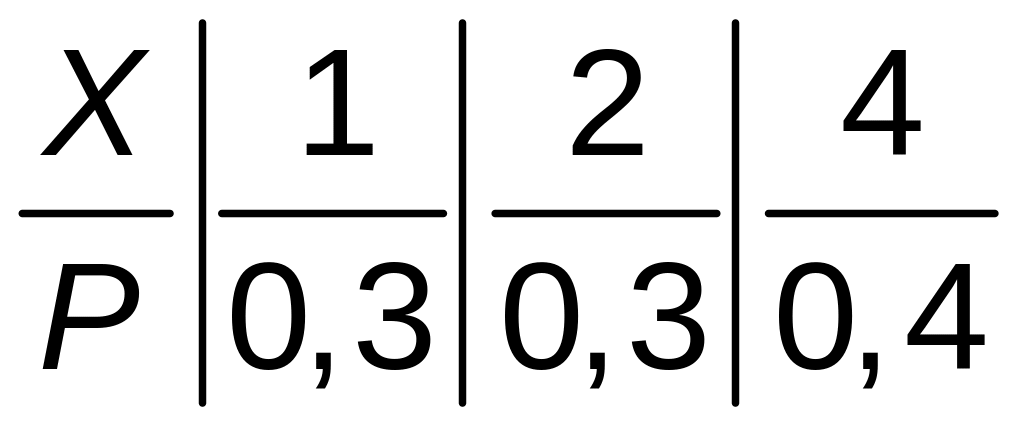
М(Х) =
D(X) = M(X - (M(X)) .
.
D(X)
= 7,9-(2,5)
.
Среднее квадратическое отклонение
Аналогично находим ряд для Y, суммируя вероятности по строкам таблицы:
.
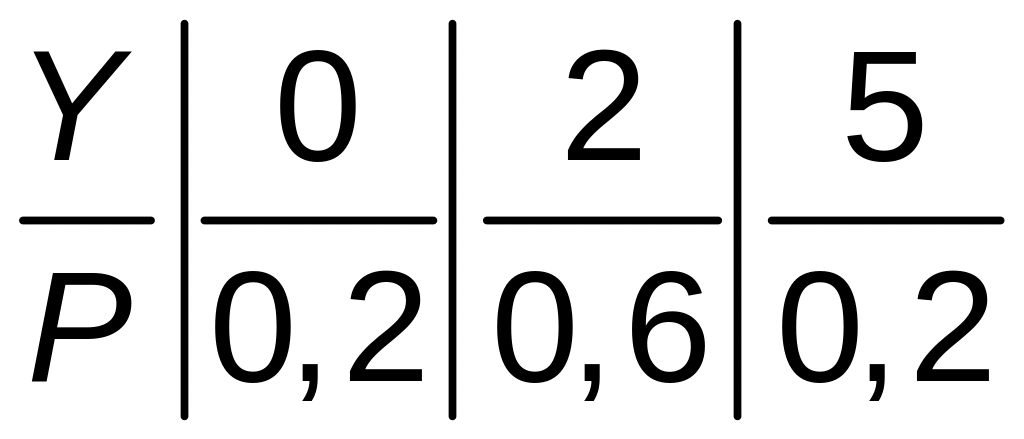M(Y)=
.
Находим математическое ожидание произведения случайных величин Х и Y:
Ковариация сov(X,Y)
= M(XY)
– M(X)M(Y)
= 4,6 – 2,5
Коэффициент корреляции определяется по формуле:
=
.
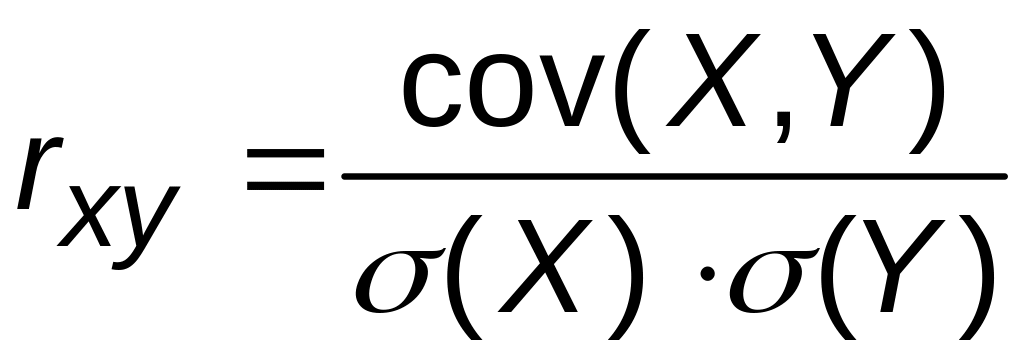Полученный результат говорит о том, что между случайными величинами Х и Y существует отрицательная линейная зависимость, т.е. при увеличении одной из них другая имеет некоторую тенденцию уменьшаться.