5. Нормальный закон распределения
Нормальный закон распределения определяется плотностью вероятности
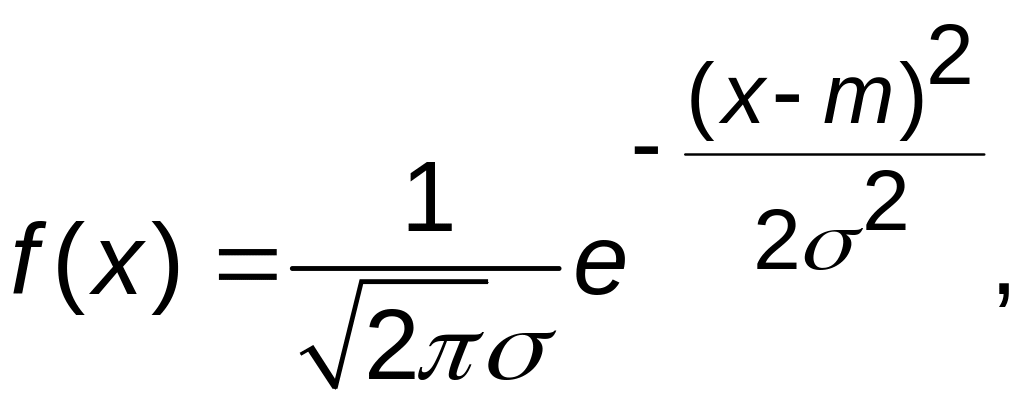(5.1)
где m и >0 – некоторые числовые параметры. В разделе 7 будут обсуждены причины, в силу которых нормальный закон распределения играет важную роль в теории вероятностей и ее приложениях.
5.1. Геометрический смысл параметров m и σ
Легко убедиться, что кривая, определяемая
функцией распределения (5.1), имеет
максимум в точке x=m,
а точки перегиба отстоят от точки x=m
на расстоянии
и при
функция (5.1) асимптотически приближается
к нулю. График функции (5.1) изображен на
рис. 5.1.
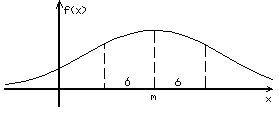
Рис. 5.1
В зависимости от величины параметров кривая плотности вероятности имеет различный вид и поэтому правильнее было бы говорить о семействе нормальных законов распределения. На рис. 5.2 показана зависимость формы кривой распределения от величины при фиксированном m.
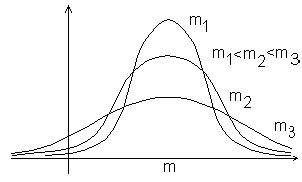
Рис. 5.2
5.2. Вероятностный смысл параметров функции распределения
Выясним теперь вероятностный смысл параметров функции распределения. Для этого вычислим математическое ожидание и дисперсию случайной величины, распределенной нормально.
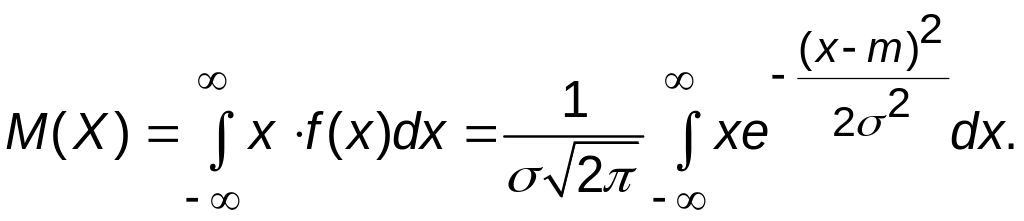
Введем новую переменную
.
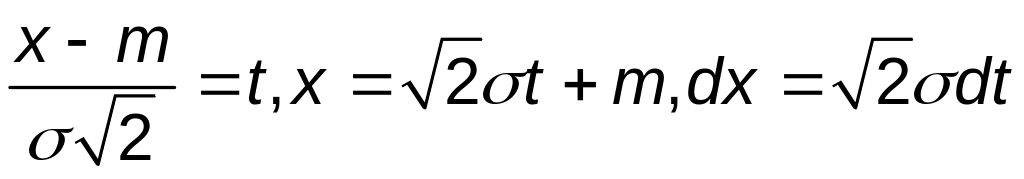Тогда
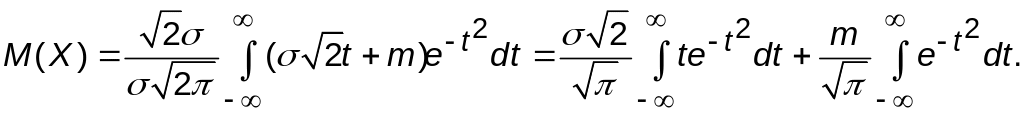
Первый интеграл равен нулю, так как под
знаком интеграла стоит нечетная функция,
а пределы интегрирования симметричны.
Второй интеграл известен как интеграл
Пуассона:
.
Поэтому M(Х)=m.
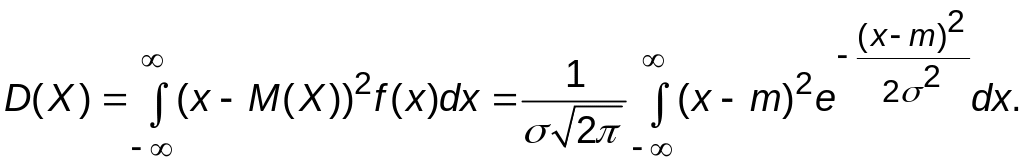
Если сделать ту же замену переменных и выполнить необходимые преобразования, то можно убедиться, что
.
Итак, параметры нормального закона
распределения m и
равны соответственно математическому
ожиданию и среднему квадратическому
отклонению случайной величины
распределенной по этому закону. Так как
параметры однозначно определяют
нормальный закон распределения, то для
нормального закона часто используют
обозначение
.
5.3. Вероятность попадания случайной величины в заданный интервал
Пусть случайная величина имеет закон распределения . Вычислим вероятность того, что она примет значение из интервала (a,b).
На основании свойств функции плотности вероятности можно записать:
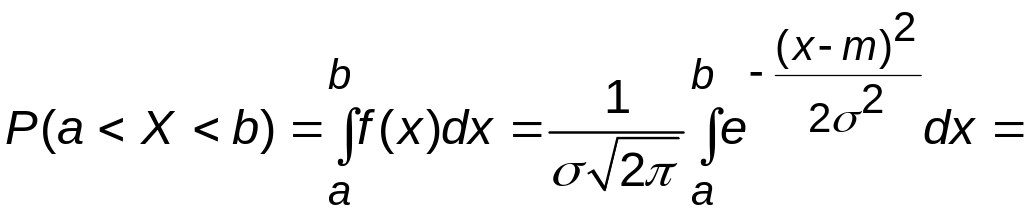
=| сделаем замену переменных
|=
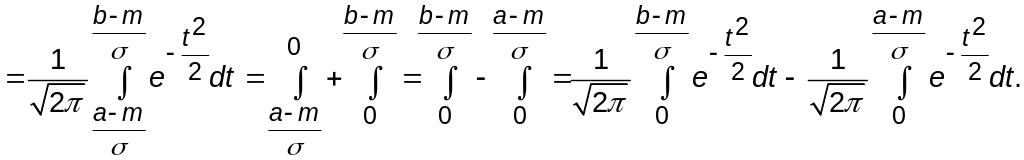
Введем в рассмотрение функцию Лапласа:
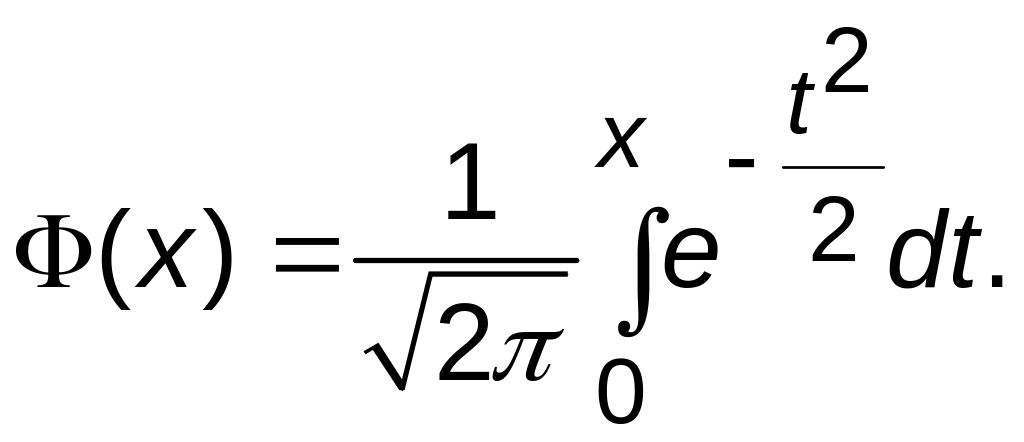
С её помощью искомую вероятность можно записать в виде
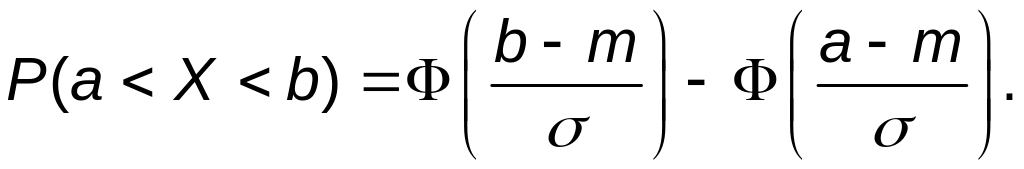(5.2)
Интеграл
в явном виде не берется, и значения
функции Ф(х) были вычислены с помощью
численных методов, а результаты сведены
в таблицу [4]. По таблице для каждого x
можно найти соответствующее значение
функции Ф(х). Функция Ф(х) нечетная,
т.е
,
графически это выглядит так (рис. 5.3).
Вследствие нечетности функции таблицы
обычно приводятся только для положительных
значений х и только из интервала
.
При значениях х>4 значения функции
Ф(х) можно брать равным 0.5.
Рис. 5.3
5.4. Вероятность отклонения случайной величины от математического ожидания
Для случайной величины, имеющей закон
распределения
,
найдем вероятность того, что отклонение
этой случайной величины от своего
математического ожидания не превысит
величины , т.е.
вычислим вероятность
Неравенство под знаком вероятности
эквивалентно неравенствам -<x-m<
или
.
Заменим в формуле (5.2)
через m-,
b – через m+,
тогда
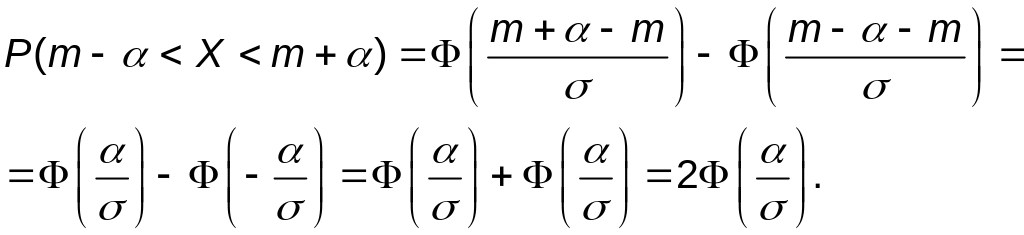
В результате получим формулу
=2
.
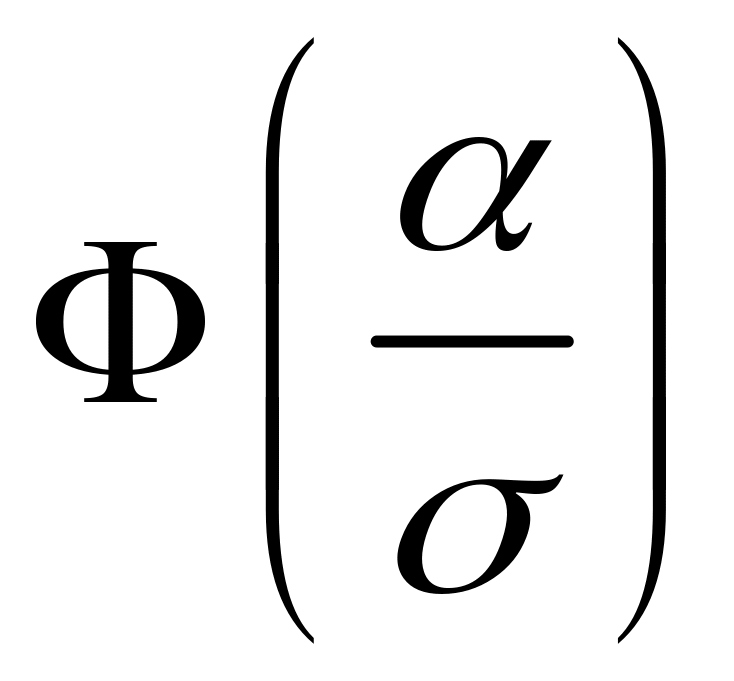(5.3)
Вероятности, определяемые формулой (5.3) применяются в теории ошибок измерений, в теории стрельб, в теории допусков и т.д. Это объясняется тем, что в этих теориях многие расчеты используют нормальный закон распределения в качестве модели для случайных ошибок, для отклонений от цели и т.д. Например, если m – расчетный размер детали, а Х – её фактический размер, то данная формула дает вероятность того, что истинный размер детали отличается от расчетного менее чем на α.
Пример 5.1.
Детали, выпускаемые цехом, по размеру диаметра распределяются по нормальному закону с параметрами: математическое ожидание равно 5 см, а дисперсия равна 0,81. Найти вероятность того, что диаметр наудачу взятой детали: а) от 4 до 7 см; б) отличается от математического ожидания не более чем на 2 см.
Решение
а) В соответствии с формулой (5.2) имеем:
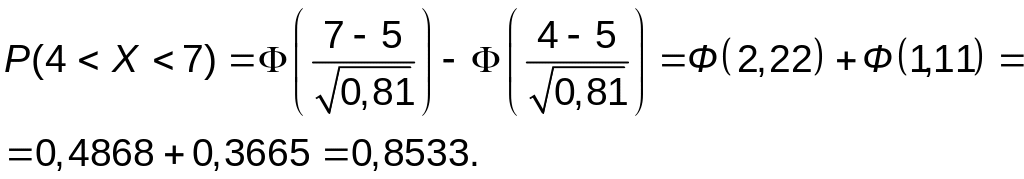
Значения Ф(2,22) и Ф(1,11) найдены по таблице значений функции Ф(х).
б) Применяя формулу (5.3) при
α=2 см,
см и m=5
см, получим
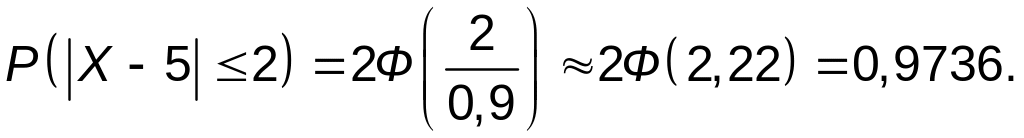
Замечание.
Для случайной величины Х
с математическим ожиданием М(Х)
и дисперсией D(Х)
случайная величина:
называется соответствующей нормированной
случайной величиной. Нормированная
случайная величина удобна тем, что
и
.
В этом можно убедиться непосредственно:
,
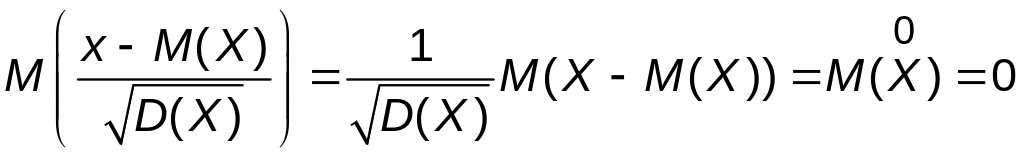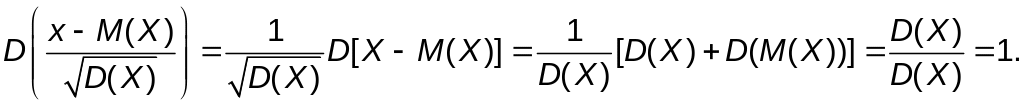
Г
Рис. 5.4
,
пронормировать, то случайная величина
будет иметь закон распределения N(0,1),
определяемый функцией плотности
вероятности
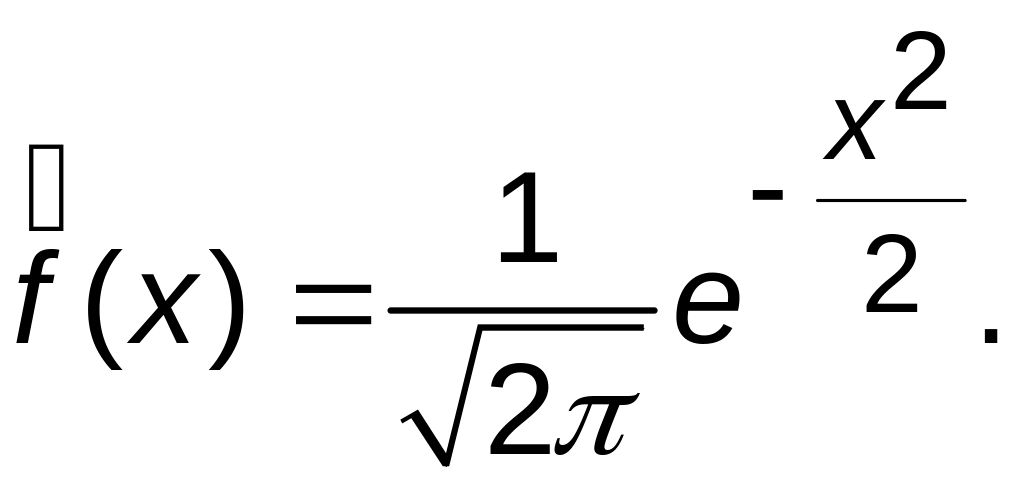
При выводе формулы (5.2)
случайная величина Х
нормировалась с помощью подстановки
.
Очевидно, что изменения масштаба не
изменяет «вероятностный механизм
явления», поэтому
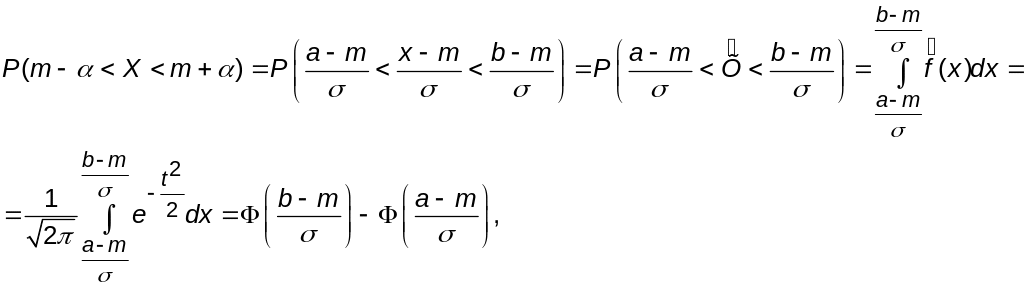
т.е. для вычисления вероятностей мы от любого закона распределения переходим к N(0,1), а для закона N(0,1) соответствующие вероятности заданы в виде таблиц функции Ф(х).