4.4. Примеры нахождения законов распределения

Рассмотрим примеры нахождения законов распределения случайных величин и их числовых характеристик.

Пример 4.7.

Составить закон распределения числа попаданий в цель при трех выстрелах по мишени, если вероятность попадания при каждом выстреле равна 0,4. Найти интегральную функцию F(х) для полученного распределения дискретной случайной величины Х и начертить ее график. Найти математическое ожидание M(X), дисперсию D(X) и среднее квадратическое отклонение (Х) случайной величины X.

Решение

1) Дискретная случайная величина Х – число попаданий в цель при трех выстрелах – может принимать четыре значения: 0, 1, 2, 3. Вероятность того, что она примет каждое из них, найдем по формуле Бернулли при: n=3, p=0,4, q=1-p=0,6 и m=0, 1, 2, 3:

.

Получим вероятности возможных значений Х: ;

;

.

Составим искомый закон распределения случайной величины Х:

Х	0	1	2	3
Р	0,216	0,432	0,288	0,064

Контроль: 0,216+0,432+0,288+0,064=1.

Построим многоугольник распределения полученной случайной величины Х. Для этого в прямоугольной системе координат отметим точки (0; 0,216), (1; 0,432), (2; 0,288), (3; 0,064). Соединим эти точки отрезками прямых, полученная ломаная и есть искомый многоугольник распределения (рис. 4.1).

х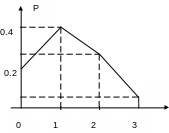

Рис. 4.1.

2) Если х 0, то F(х)=0. Действительно, значений, меньших нуля, величина Х не принимает. Следовательно, при всех х 0 , пользуясь определением F(х), получим F(х)=P(X<x)=0 (как вероятность невозможного события).

Если 0<x , то F(X)=0,216. Действительно, в этом случае F(х)=P(X<x)= = P(- <X 0)+P( 0<X<x)=0,216+0=0,216.

Если взять, например, х=0,2, то F(0,2)=P(X<0,2). Но вероятность события Х<0,2 равна 0,216, так как случайная величина Х лишь в одном случае принимает значение меньшее 0,2, а именно 0 с вероятностью 0,216.

Если 1<x , то

Действительно, Х может принять значение 0 с вероятностью 0,216 и значение 1 с вероятностью 0,432; следовательно, одно из этих значений, безразлично какое, Х может принять (по теореме сложения вероятностей несовместных событий) с вероятностью 0,648.

Если 2<x , то рассуждая аналогично, получим F(х)=0,216+0,432 + + 0,288=0,936. Действительно, пусть, например, х=3. Тогда F(3)=P(X<3) выражает вероятность события X<3 – стрелок сделает меньше трех попаданий, т.е. ноль, один или два. Применяя теорему сложения вероятностей, получим указанное значение функции F(х).

Если x>3, то F(х)=0,216+0,432+0,288+0,064=1. Действительно, событие X является достоверным и вероятность его равна единице, а X>3 – невозможным. Учитывая, что

F(х)=P(X<x)=P(X 3) + P(3<X<x), получим указанный результат.

Итак, получена искомая интегральная функция распределения случайной величины Х:

F(x)=

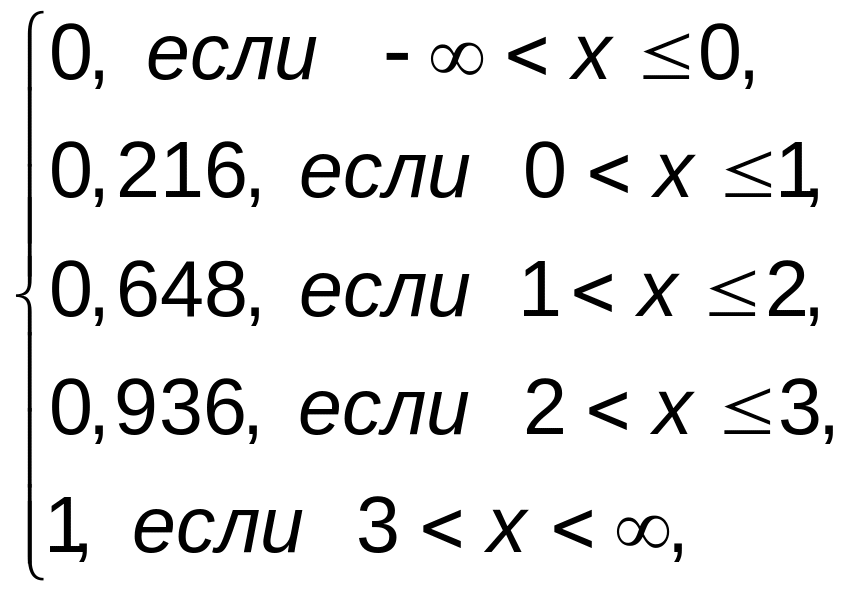
график которой изображен на рис. 4.2.

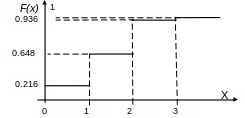
Рис. 4.2

3) Математическое ожидание дискретной случайной величины равно сумме произведений всех возможных значений Х на их вероятности:

М(Х)=0 =1,2.

То есть, в среднем происходит одно попадание в цель при трех выстрелах.

Дисперсию можно вычислить, исходя из определения дисперсии D(X)=M(X-M(X)) или воспользоваться формулой D(X)=M(X , которая ведет к цели быстрее.

Напишем закон распределения случайной величины Х :

Х2	0	1	4	9	.
Р	0,216	0,432	0,288	0,064

Найдем математическое ожидание для Х :

М(Х ) = 0 4 = 2,16.

Вычислим искомую дисперсию:

D(X) = M(X ) – (M(X)) = 2,16 – (1,2) = 0,72.

Среднее квадратическое отклонение найдем по формуле

(X) = = 0,848.

Интервал (M- ; M+ ) = (1,2-0,85; 1,2+0,85) = (0,35; 2,05) – интервал наиболее вероятных значений случайной величины Х, в него попадают значения 1 и 2.

Пример 4.8.

Дана дифференциальная функция распределения (функция плотности) непрерывной случайной величины Х:

f(x)=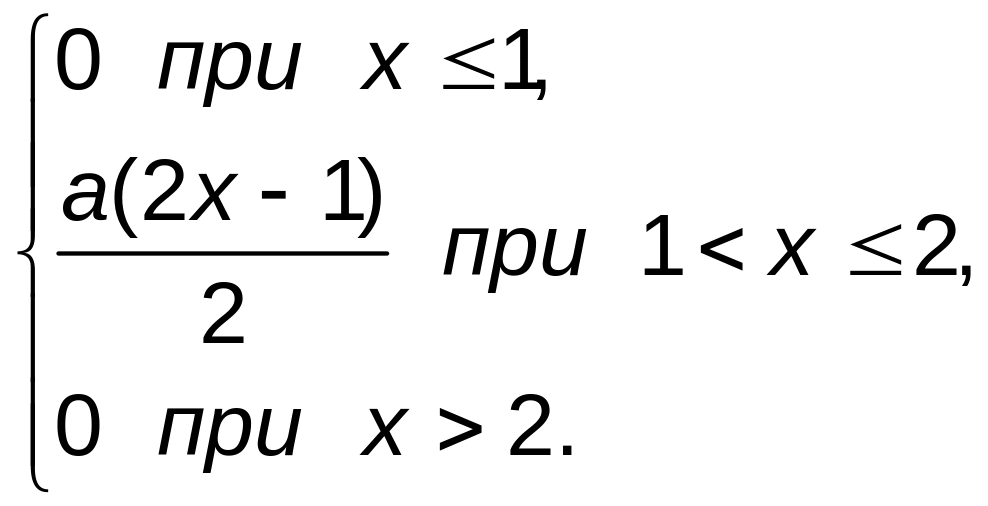

1) Определить постоянный параметр a.

2) Найти интегральную функцию F(x).

3) Построить графики функций f(x) и F(x).

4) Найти двумя способами вероятности Р(0,5<X 1,5) и P(1,5<X<3,5).

5). Найти математическое ожидание М(Х), дисперсию D(Х) и среднее квадратическое отклонение случайной величины Х.

Решение

1) Дифференциальная функция по свойству f(x) должна удовлетворять условию .

Вычислим этот несобственный интеграл для данной функции f(x):

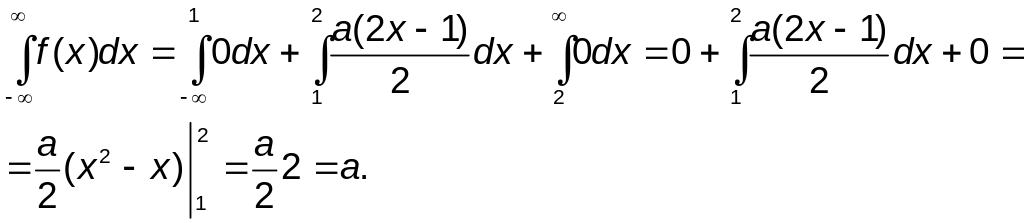
Подставляя этот результат в левую часть равенства, получим, что а=1. В условии для f(x) заменим параметр а на 1:

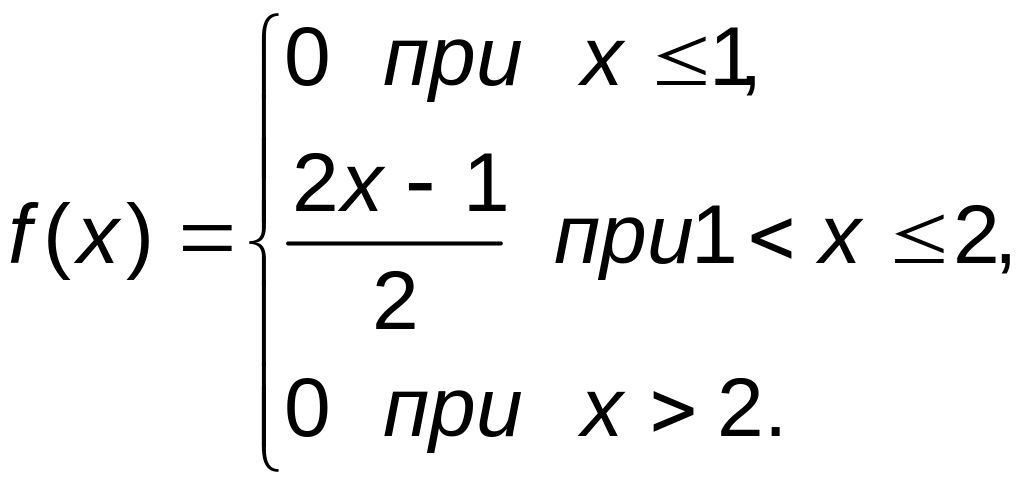
2) Для нахождения F(x) воспользуемся формулой

.

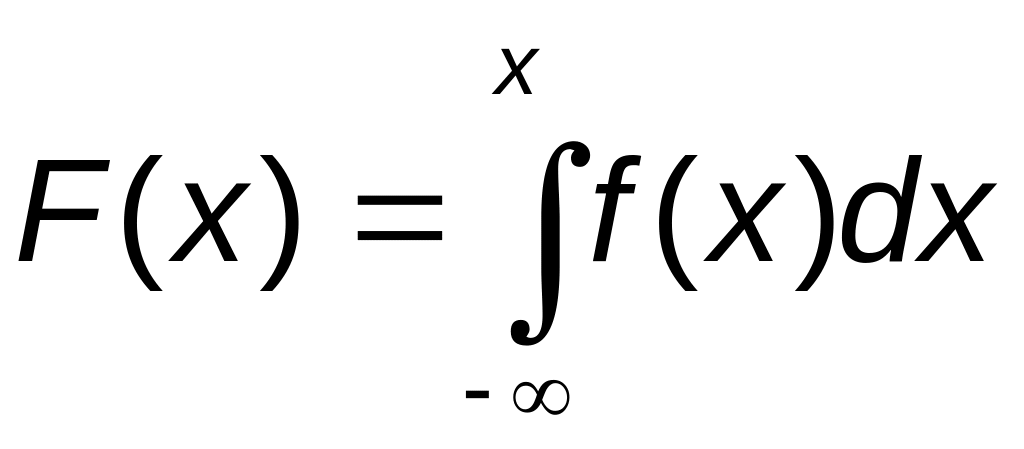Если х , то , следовательно,

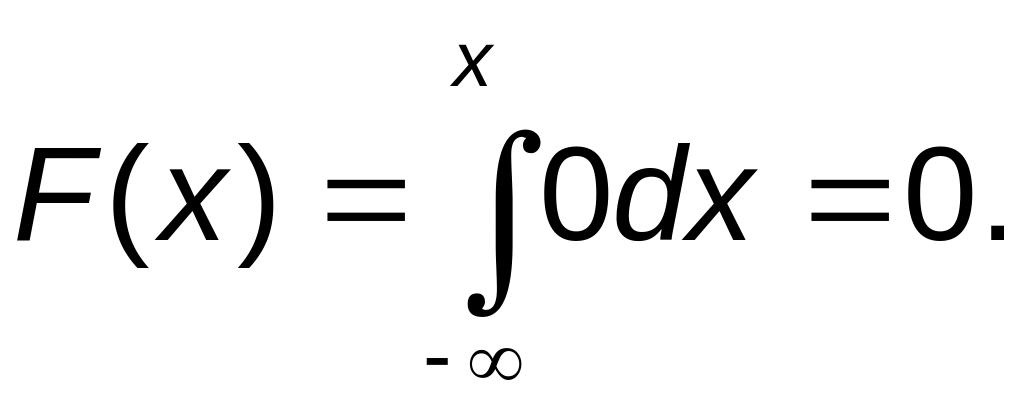
Если 1 то

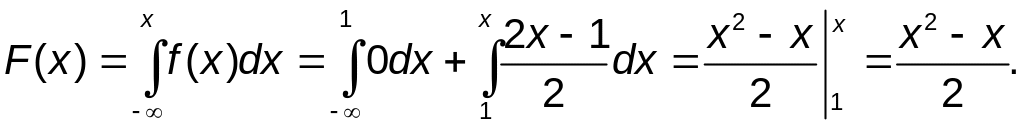
Если x>2, то

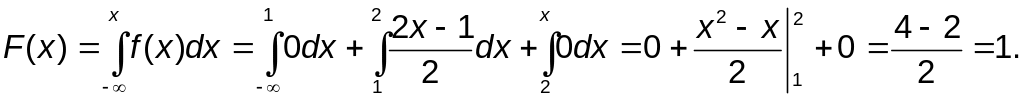
Итак, искомая интегральная функция F(x) имеет вид:

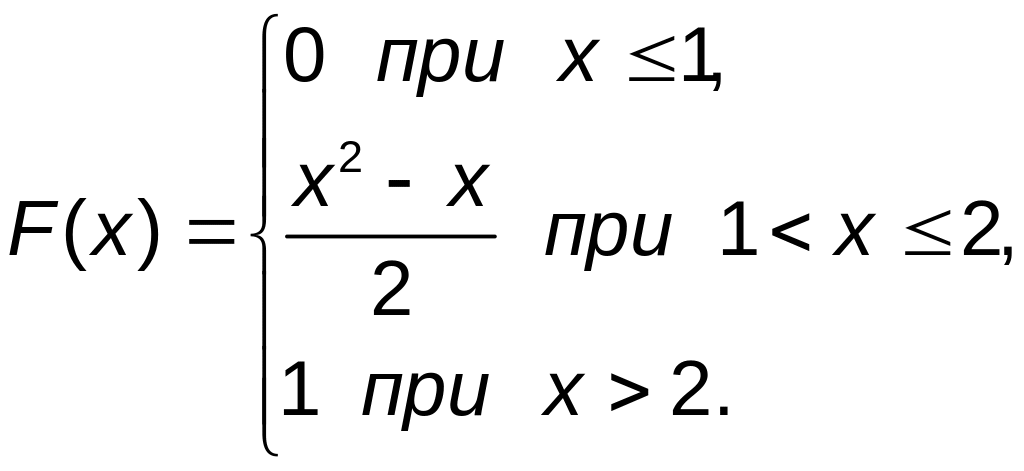
3) Построим графики функций f(x) и F(x) (рис. 4.3 и 4.4).

Рис. 4.3

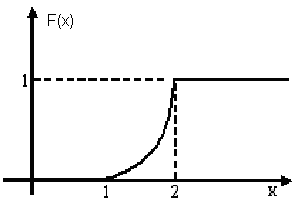
Рис. 4.4.

4) Вероятность попадания случайной величины в заданный интервал (а,b) вычисляется по формуле 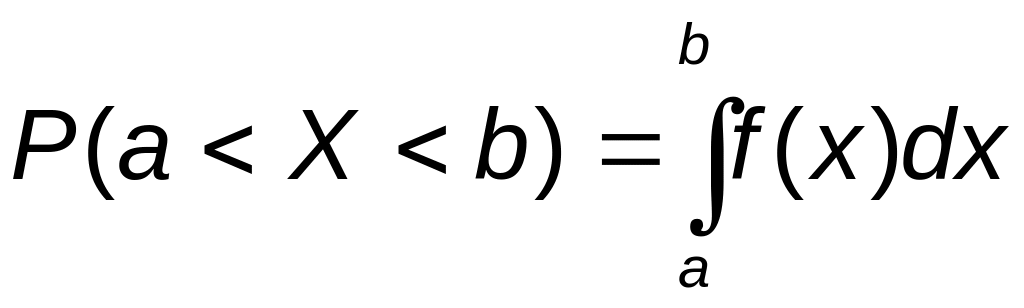, если известна функция f(x), и по формуле P(a < X <b) = F(b) – F(a), если известна функция F(x).

Найдем по двум формулам и сравним результаты. По условию а=0,5; b=1,5; функция f(X) задана в пункте 1). Следовательно, искомая вероятность по формуле равна:

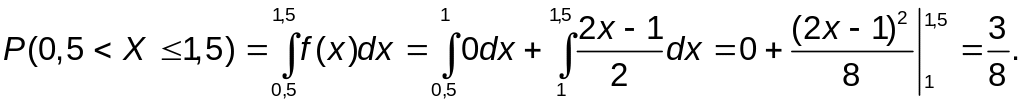
Та же вероятность может быть вычислена по формуле b) через приращение полученной в п.2). интегральной функции F(x) на этом интервале:

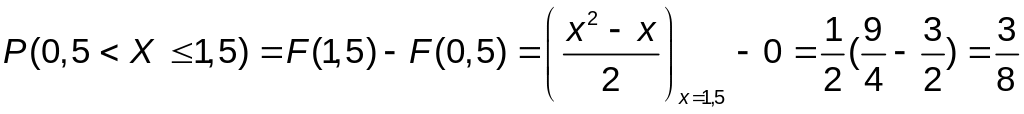, так как F(0,5)=0.

Аналогично находим

,

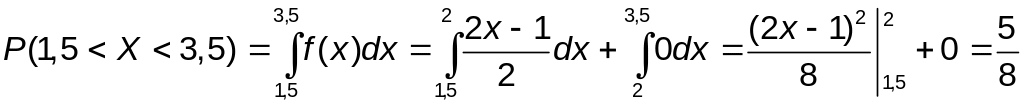или

,

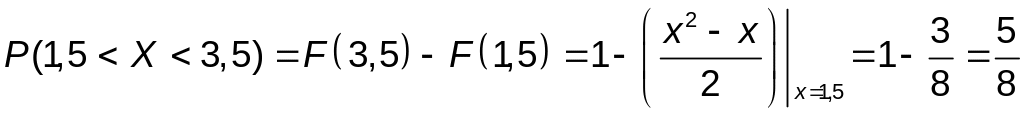так как F(3,5)=1.

5) Для нахождения математического ожидания М(Х) воспользуемся формулой 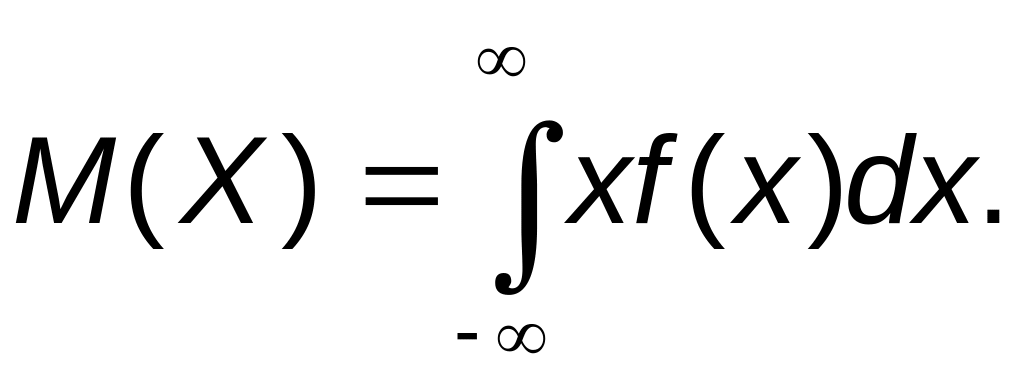Функция f(x) задана в решении пункта 1), она равна нулю вне интервала (1,2]:

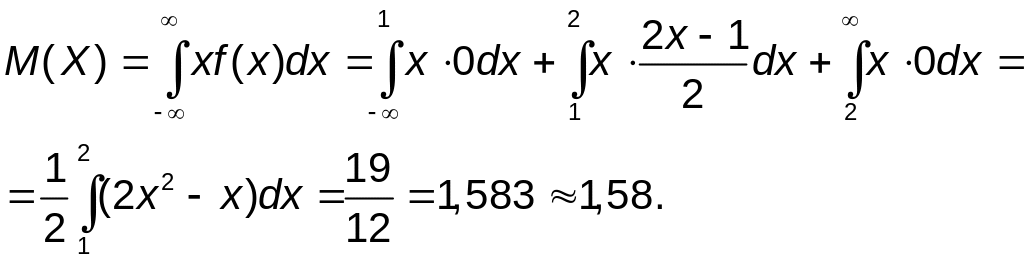
Дисперсия непрерывной случайной величины D(Х) определяется равенством

, или равносильным равенством

.

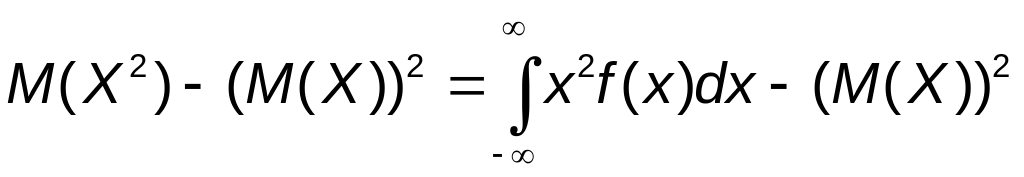Для нахождения D(X) воспользуемся последней формулой и учтем, что все возможные значения f(x) принадлежат интервалу (1,2]:

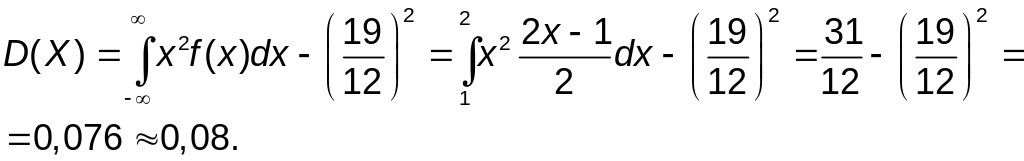
Среднее квадратическое отклонение = =0,276.

Интервал наиболее вероятных значений случайной величины Х равен

(М- ,М+ ) = (1,58-0,28; 1,58+0,28) = (1,3; 1,86).