3.2. Законы распределения дискретных случайных величин

Так как дискретная случайная величина имеет конечное или счётное множество значений, то их можно просто перечислить и указать соответствующие вероятности. Это можно сделать, например, в форме таблицы

X			…		…
P	р1	р2	…	рn	…	,

где – вероятность того, что X примет значение x_i.

Такую таблицу называют рядом распределения.

События … несовместимы, и в результате опыта одно из них обязательно происходит. Из этого следует

Для наглядности ряд распределения можно изобразить геометрически. Для этого из каждой точки откладывают вверх отрезок равный (рис. 3.1).

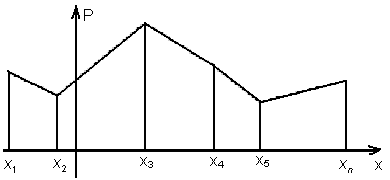
Рис. 3.1.

Пример 3.2. Индикатор события I. Эта случайная величина имеет закон распределения:

I	0	1
P	q	р

Если вероятность появления события в некотором опыте равна p, то I принимает значение 1, если событие произошло, и значение 0, если событие не произошло. I можно назвать числом появлений события в одном опыте.

Пример 3.3.

Биномиальный закон распределения. Случайная величина может принимать значения 0,1,2,…,n, и каждому значению X=m соответствует вероятность , где p+q=1. Этот закон распределения считается заданным, если известны числа n и p, через которые выражаются все вероятности. Случайную величину, подчинённую этому закону, можно назвать числом появлений события в n независимых опытах.

Пример 3.4.

Пуассоновский закон распределения. Случайная величина имеет возможные значения 0,1,2,3,…, и каждому значению Х=m соответствует вероятность 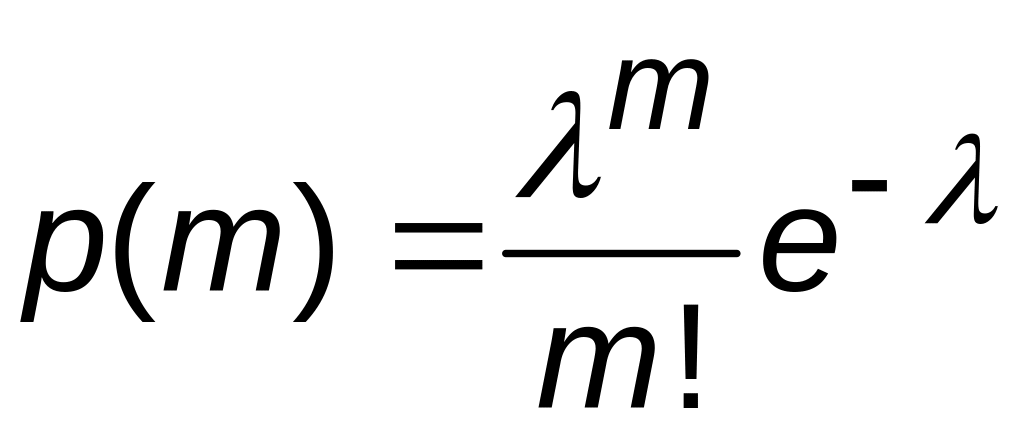, где  – некоторый параметр, вероятностный смысл которого будет указан позже.

Пример 3.5.

Гипергеометрический закон распределения. Возможные значения X: 0,1,…,n. И каждому значению X=m соответствует вероятность P(X=m)=P = 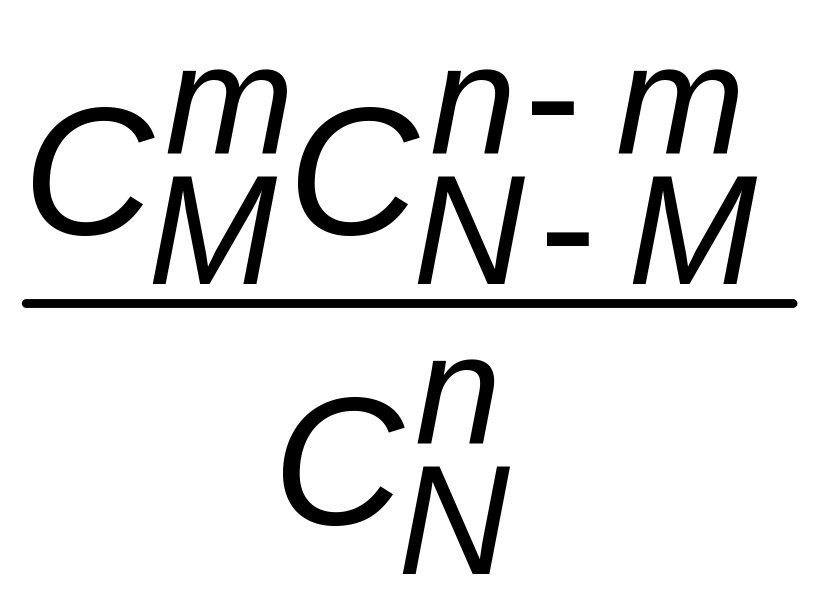. Эта случайная величина, например, равна числу m бракованных изделий среди n взятых наугад из партии объёма N, содержащей M бракованных изделий.

Пример 3.6. Геометрический закон распределения.

X	1	2	3	…	n	…
P	p	qp		…		…

Если, например, p – вероятность изготовления бракованной детали, то случайная величина X с этим законом распределения будет равна общему числу деталей до момента изготовления первой бракованной детали.

Построение ряда распределения удобно лишь для дискретных случайных величин, так как можно перечислить все возможные их значения.

3.3. Законы распределения непрерывных случайных величин

3.3.1. Интегральная функция распределения

Все по отдельности возможные значения непрерывных случайных величин перечислить нельзя – их бесконечно много. Поэтому естественно указывать вероятности не для отдельных значений, а для целых интервалов. Рассмотрим значения случайной величины Х такие, что Х<х. Вероятность события X<х зависит от x, т.е. является функцией x. Эта функция и называется интегральной функцией распределения или просто функцией распределения случайной величины и обозначается через F(х). Итак, по определению

F(х)=P(X<x).

Для наглядности можно представить себе такую картину. На числовую ось наугад бросаем точку (в соответствии с некоторым законом распределения). Тогда F(х) для каждого x указывает вероятность того, что точка упадёт левее x

Непосредственно из определения интегральной функции распределения вытекают следующие свойства F(х):

1. . Это следует из того, что F(х)=P(X<x), а вероятность P – есть число, заключённое между нулём и единицей.

Нетрудно видеть, что , так как события X<- и X< являются соответственно невозможными и достоверными.

2. Интегральная функция распределения является неубывающей, т.е. при . В самом деле, пусть . Событие можно разложить на два события: и . События эти несовместны, поэтому по теореме сложения вероятностей имеем

или

.

Так как в правой части стоит неотрицательная величина, то

Следствие 1. Вероятность того, что случайная величина X примет значение из интервала [a,b], равна приращению интегральной функции распределения на этом интервале:

Следствие 2. Если функция F(х) непрерывна, то вероятность того, что непрерывная случайная величина примет одно единственное значение, равна нулю. Это следует из того, что

при x0, следовательно,

Р(х Р(Х=х)=0.

Можно провести следующую аналогию. Геометрическая точка не имеет размера, а интервал, состоящий из точек, имеет длину, отличную от нуля. Так и для непрерывных случайных величин одно единственное значение имеет нулевую вероятность, а интервал имеет вероятность, отличную от нуля. В общем случае график функции F(х) изображен на рис. 3.2. Если рассмотреть на оси Ох интервалы одинаковой длины, то вероятность попасть в какой-то из них для случайной величины Х будет тем больше, чем больше окажется приращение функции F(х) на этом интервале.

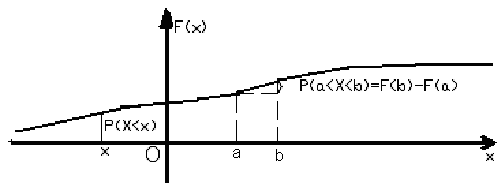
Рис. 3.2