Геометрические вероятности

Определение 1. Дано некоторое испытание с пространством элементарных исходов Ω. И Ω представлено либо в виде тела в пространстве, либо в виде плоской фигуры, либо в виде отрезка на прямой. Пусть известно, что вероятность любого события А зависит только от размера множества А, но не зависит от местоположения А в Ω. Тогда

(4.5)  , где μ – мера множества, т.е. объем в случае пространства, площадь в случае плоскости, длина в случае отрезка.

Теорема 3. Формула 4.5 действительно задает вероятность, т.е. выполняются свойства теоремы 1 §2.

Доказательство:

Проверим свойства теор.1.

1: надо проверить, что Р(А) ≥ 0.

по (4.5)  ≥ 0, т.к числитель и знаменатель не отрицательны.

2: проветим, что Р(Ω) = 1.

3: Для несовместимых событий

Пример 1. Между пунктами А и В проложен телефонный кабель длиной 10 км. На линии произошел разрыв. Из пункта А выехала ремонтная бригада, которая обследует линию со скоростью 5 км/ч. Найти вероятность того, что обрыв будет найден за полчаса.

Решение:

Представим пространство элементарных исходов в виде отрезка. Обрыв – любая точка на этом отрезке. Обозначим ее ω. Рассмотрим произвольный отрезок Н. Вероятность попадания точки в этот отрезок зависит только от длины отрезка и не зависит от его местоположения на отрезке [А,В]. Следовательно, для вычисления вероятности можем применить формулу 4.1.

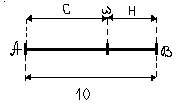
В данном случае μ – длина. За полчаса бригада проедет 2.5 км. Тогда

Р {обрыв найдут за 0.5.ч.} = 

Пример 2. Два человека договорились встретиться в определенном месте от 12 до 13 ч . Причем каждый приходит к месту встречи в случайное время между 12 и 13 часами, ждет 20 мин, а затем уходит. Найти вероятность того, что встреча состоится.

Решение:

Пусть х – время прихода 1-го человека, у – время прихода 2-го,

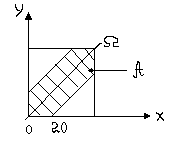
0 ≤ х ≤ 60 мин., 0 ≤ у ≤ 60 мин.

W можно представить как квадрат на плоскости. Для удобства мы перенесли начало координат в точку (12,12). Тогда событие А={встреча состоится}={(x,y), |х – у| ≤ 20 мин.}

Т. к люди приходят в случайное время, то вероятность попадания в любое множество зависит только от его площади.

m (Ω)= 60², m (Α) = 60²–40². Тогда вероятность 

Задание вероятности на дискретном пространстве элементарных исходов

Определение 2. Множество называется дискретным, если оно конечное или счетное.

Теорема 4. Пусть дано дискретное пространство элементарных исходов Ω и пусть задана функция Р(ω), удовлетворяющая следующим условиям:

1) Р(ω) ≥ 0

2) 

Тогда равенство

(4.6)   задаёт вероятность

Доказательство:

Проверим три свойства из теор.1 §2.

1)  , т.к все Р(ω) ≥ 0, следовательно, Р(А) ≥ 0.

2) Р(Ω) = 1 из свойства 2.

3) если А и В несовместны, то Р(А + В) = Р(А) + Р(В). Проверим:

Т .к множества А и В не пересекаются.

Пример 3. Вероятность выигрыша по 1 билету лотереи равна 0.1. Некто решил покупать билеты до тех пор, пока не выиграет. Найти вероятность того, что он потратит меньше, чем 20 рублей, если билет стоит 5 рублей.

Решение: Мы уже выписывали пространство элементарных исходов для такой задачи:

Ω = {В, НВ, ННВ,НННВ,…}

Обозначим эти исходы соответственно ω₁, ω₂, ω₃, … ω_i,….

Известно, что Р(ω₁) = 0.1

Функцию Р(ω) предлагается задать следующим образом:

Р(ω₂) = (1 – 0,1)× 0,1 = 0,09

Р(ω₃) = (1 – 0,1)^2× 0,1 = 0,081

……….

Р(ω_i) =(1 – 0,1) ^(i-1) ∙ 0,1.

Проверим выполнение свойств 1 и 2 теоремы 4:

1: Р(ω_i) ≥ 0

2: Σ Р(ω_i) = 0.1 ∙ 0.9º + 0.1∙ 0.9¹ + 0.1 ∙ 0.9 ²+ …= 0.1(1 + 0.9 + 0.9²+…) =

в скобках получилась бесконечная геометрическая прогрессия со знаменателем 0,9, её сумма вычисляется по соответствующей формуле

=  Свойство 2 выполняется.

Найдем вероятность нашего события :

А = { потратит меньше 20 руб.} = {купит не больше 3-х билетов} =

{ω1, ω2, ω3}

Аксиоматическое определение вероятности.

Определение 3. Пусть дано пространство элементарных исходов Ω. Пусть функция Р(А) определена на элементах этого пространства. Функция Р(А) называется вероятностью, если выполняются следующие свойства:

А1) Р(А) ≥ 0 " А (каждому событию А соответствует положительное число).

А2) Р(Ω) = 1 (вероятность достоверного события равна 1)

А3) Для несовместных событий Р(А + В) = Р(А) + Р(В)

Свойство А1) также называют аксиомой положительности, А2) – аксиомой нормированности, А3) – аксиомой аддитивности.

Будем также использовать обобщение свойства А3:

Пусть А₁ , А₂, …, А_n – счетное множество попарно несовместных событий, т.е А_i ∙ А_j = Ø при i ≠ j. Тогда 

В дальнейшем, при проверке того, задает ли некоторая функция вероятность, будем проверять свойства А1, А2, А3.