Задачи для самоконтроля к §9

1. Станок – автомат выпускает 30% деталей высшего сорта. Найти вероятность того, что из 6 случайно отобранных деталей будет:

а) 4 высшего сорта; б) хотя бы 4 высшего сорта.

2. Что более вероятно выиграть у равносильного противника:

а) три партии из четырёх или хотя бы три из пяти;

б) три партии из четырёх или пять из восьми;

3. Вероятность выиграть хотя бы по одному лотерейному билету из трёх равна 0,271. Какова вероятность выиграть по всем трём билетам?

§ 10 Предельные теоремы в схеме Бернулли.

Предположим, что вероятность успеха в испытаниях по схеме Бернулли равна 0,1. Требуется вычислить вероятность того, что в 1000 испытаниях успехов будет 500. По формуле Бернулли такая вероятность равна

Однако вычислить значение такого выражения практически невозможно. Получается, что пользоваться формулой Бернулли при больших n достаточно трудно, т.к. числа там получаются и громадные и очень маленькие. Возникает вопрос, нельзя ли как - то упростить вычисления?

10.1 Локальная теорема Муавра – Лапласа.

Теорема 1. Пусть проводятся испытания по схеме Бернулли, при этом вероятность успеха “достаточно большая” – 0,1 < p ≤ 0,9. Кроме того, произведение n ∙ p ∙ q ≥ 9. При этих условиях, а так же при конечном, но достаточно большом n (порядка нескольких десятков), справедлива приближенная формула Муавра-Лапласа (локальная):  10.1

Функция φ (х) протабулирована, кроме того легко вычисляется на компьютере или на калькуляторе. Среди нужных нам свойств функции

φ(х) отметим два :

1) φ(х) – чётная функция, т.е. φ(х) = φ(-х);

2) 

Замечание : Эта приближённая формула тем точнее, чем больше n и чем ближе вероятность успеха p к 0,5.

Пример 1. Игральную кость бросают 80 раз. Найти вероятность того, что цифра 4 появится 20 раз.

Решение: выполняются условия схемы Бернулли, n = 80 ; k = 20.Найти надо P₈₀(20) т.е. вычислить вероятность по формуле Бернулли сложно. Проверим условия применимости формулы 10.1:

p = 1/6 = 0,1(6) > 0,1; n ∙ p ∙q = 80 ∙ (1/6) ∙ (5/6) = 400/36 > 9 , n – достаточно большое, т.е. можем применить формулу 10.1. Тогда

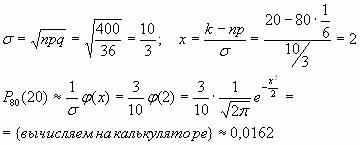
10.2 Интегральная теорема Муавра – Лапласа.

Теорема 2. В условиях предыдущей теоремы вероятность того, что в n испытаниях успехов будет от k₁ до k₂ включительно, приближенно вычисляется по формуле:

10.2 P_n(k₁,k₂) = Ф₀ (х₂) – Ф₀ (х₁), где

Ф₀ (х)=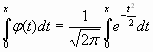 – интеграл Лапласа

Формулу 10.2 называют интегральной формулой Муавра – Лапласа.

Для вычисления Ф0 (х) пользуются специальными таблицами, т.к этот интеграл “не берется” (не выражается через элементарные функции). Часто эта функция присутствует в современных калькуляторах, всегда есть в электронных таблицах, например, в Excel.

Свойства функции Ф0 (х):

1. Эта функция нечётная, т.е. Ф0 (-х) = –Ф0 (х);

2. Ф0 (х) = 0.5, если х> 5, поэтому в таблице значений функции при x>5 нет.

Пример 2. Игральную кость бросают 80 раз. Найти вероятность того, что “4” выпадет не более 20 раз. Т.е. надо найти P₈₀(0,20). В примере 1 мы уже проверили, что условия применимости формулы 10.2 выполняются, тогда

Р₈₀ (0,20) = Ф₀ (х₂) – Ф₀ (х₁) = Ф₀ (2) – Ф₀ (–4) = Ф₀ (2) + Ф₀ (4) =

{смотрим по таблице значения фукции Ф₀ }= 0,4772 + 0,4999 = 0,9771.