6.2 Функция распределения двумерной случайной величины.

Дана двумерная случайная величина (ξ, η). Как уже говорилось, её функция распределения определяется равенством: F(ξ, η)(x,y) = P {ξ < x, η < y} ( в дальнейшем будем писать просто F(x,y) ). Т.е. это вероятность попадания случайной точки с координатами (ξ, η) в бесконечный квадрант с вершиной в точке (x,y).

Теорема 1( свойства функции распределения двумерной с.в.).

1. 0 ≤ F(x,y) ≤ 1.

2. F(x,y) – неубывающая функция по каждому аргументу.

3. F (–∞, y) = 0, F(x , – ∞) = 0, F(–∞, –∞) = 0, F(∞, ∞) = 1.

4. F(x , ∞) = F_ξ(x), F(∞, y) = Fh (y)

5. Вероятность попадания случайной точки (ξ, η) в прямоугольник P {x₁ ≤ ξ ≤ x₂, y₁ ≤ η ≤ y₂ } = F(x₂,y₂) – F(x₁,y₂) – F(x₂,y₁) + F(x₁,y₁)

Доказательство:

1) т.к это вероятность, а она всегда неотрицательна.

2) “Неубывающая по каждому аргументу” означает, что:

если х₁ < х₂   F(x₁, y) ≤ F(x₂,y);

если y₁ < y₂  F(x,y₁) ≤ F(x,y₂).

Докажем, что функция неубывающая по переменной х:

Пусть х₁ < х₂. Разобьём событие {ξ < х₂, η < у} на два непересекающихся:

 

Тогда 

По определению 1 это

Т.к. 

Аналогично доказывается неубывание по переменной у.

3) Докажем первое равенство, остальные доказываются аналогично:

F (–∞, y) = 0.

По определению 1 это Р {ξ < –∞, η < у} = Р{Ø} = 0.

4) F(x , ∞) = Р {ξ < х, η < ∞} = Р{ξ < х} = F_ξ(x).

Второе утверждение доказывается аналогично.

5) Геометрически получаем вероятность попадания в прямоугольник путём вычитания вероятностей попадания в квадранты. При этом вероятность попадания в квадрант с вершиной в точке (x₁,y₁) вычтем дважды, поэтому её надо прибавить

P {x₁ ≤ ξ ≤ x₂, y₁ ≤ η ≤ y₂ } = F(x₂,y₂) – F(x₁,y₂) – F(x₂,y₁) + F(x₁,y₁)

6.3 Непрерывные двумерные случайные величины.

Определение 3. Пусть (ξ, η) – непрерывная двумерная случайная величина. Она, кроме функции распределения, может быть задана двумерной ( совместной ) плотностью распределения р(x,y).

В свою очередь, функцию распределения можно найти как

Теорема 2 (свойства плотности распределения)

1) Р(x,y) ≥ 0.

2) 

3) 

4)   , 

Пример 2. Плотность распределения системы двух случайных величин ξ и η задаётся следующим выражением:

Найти:

1) коэффициент а;

2) функцию распределения;

3) плотности каждой из компонент;

4) вероятность попадания в квадрат   .

Решение:

1) Воспользуемся свойством 2 теоремы 2:

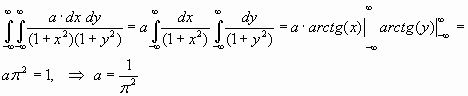
2)

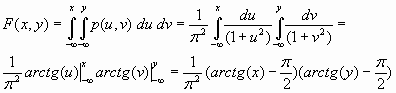
3)

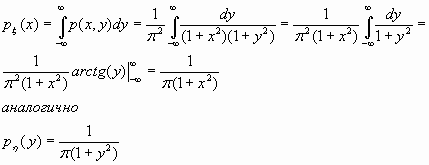
4) вероятность 

Вычислим эти величины отдельно:

Подставим эти значения и получим :

§7 Ковариация и корреляция.

Определение 1. Пусть дана двумерная с.в. (ξ, η) ( или две одномерные случайные величины ξ и η). Ковариация случайных величин ξ, η определяется равенством:

cov (ξ, η) = M [(ξ – M ξ)( η – M η)]

Иногда используют обозначение к(ξ, η).

Теорема 1(свойства ковариации)

1) сov (ξ, ξ) = Dξ

2) сov (ξ, η) = M(ξ× η) – Mξ× Mη

3) если ξ, η – независимы, то сov (ξ, η) = 0 ( независимость трактуется как отсутствие взаимного влияния друг на друга, и отсутствие причин, влияющих на обе случайные величины)

Доказательство:

1) по определению 1: cov (ξ, ξ) = M[(ξ - M ξ)( ξ - M ξ)] = M[(ξ - M ξ)²] = Dξ

2) сov (ξ, η) = M [(ξ – M ξ)( η – M η)] = M[ξ× η – η× Mξ – ξ× Mη + Mξ× Mη] =

M (ξ× η) – Mξ× Mη – Mξ× Mη + Mξ× Mη = M(ξ× η) – Mξ× Mη.

3)если ξ, η – независимы, то по свойству мат. ожидания, M(ξ× η) = Mξ× Mη. Тогда сov (ξ, η) = M(ξ × η) – Mξ× Mη = Mξ× Mη– Mξ× Mη= 0.

Формулы для вычисления ковариации

Если ξ, η – дискретные с.в., ξ принимает значения из множества {х₁, х₂, …x_n}, η принимает значения из множества {y₁, y₂, …..y_k}, и P_ij = P{ξ = x_i, η = y_j}, то ковариацию вычисляют по формуле

Если ξ, η – непрерывные с.в., и p(x,y) – совместная плотность (ξ, η), тогда ковариацию вычисляют по формуле

Определение 2 . Пусть дана двумерная с.в.(ξ, η) ( или две одномерные случайные величины ξ и η). Коэффициент корреляции ξ и η вычисляется по формуле:

Теорема 2 (свойства коэффициента корреляции)

1. если ξ, η – независимы, то ρ(ξ, η) = 0

2. –1 ≤ ρ(ξ, η) ≤ 1

3. Пусть даны случайные величины ξ и η, причём η = аξ + в, где а,в– некоторые константы (т.е. η линейно зависит от ξ). Тогда ρ(ξ, η) равен либо 1, либо –1.

Замечание: Коэффициент корреляции – это количественная мера линейной зависимости между случайными величинами. Если с.в. независимы, то он равен 0. Если зависимость прямая, т.е. при возрастании ξ, возрастает η, то коэффициент корреляции положительный.Если при возрастании ξ, η убывает, то коэффициент корреляции отрицательный. Чем ближе коэффициент корреляции к границе: к –1 или к 1, тем зависимость сильнее.

Определение 3. Пусть даны случайные величины ξ₁, ξ₂, ….ξ_n . Матрица ковариаций состоит из элементов k_ij = cov (ξ_i, ξ_j), i=1,..n, j=1,...n.

К = 

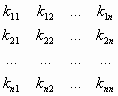
Cвойства матрицы ковариаций:

1) Т.к. cov (ξ_i, ξ_j) = cov (ξ_j, ξ_i), то матрица симметрична относительно главной диагонали.

2) cov (ξ_i, ξ_i) = Dx _i , т.е. на главной диагонали стоят дисперсии соответствующих случайных величин.

Определение 4. Пусть даны случайные величины ξ₁, ξ₂, ….ξ_n Матрица коэффициентов корреляции состоит из элементов ρ _ij = ρ (ξ_i, ξ_j), i=1,..n, j=1,...n.

R = 

Свойства корреляционной матрицы:

1) Она также симметрична относительно главной диагонали.

2) ρ _ii =1(по диагонали стоят 1)

Пример 1. Рассмотрим три случайные величины: ξ₁ – стипендия в 1-м семестре,

ξ₂ – стипендия в 2-м семестре, ξ₃ – стипендия в 3-м семестре (числа не соответствуют действительности, они подбирались из соображений простоты вычислений). Дана матрица ковариаций этих случайных величин:

К=

Найти : 1) дисперсии этих случайных величин; 2) матрицу коэффициентов корреляции.

Решение:

1) Dξ₁ = cov (ξ₁, ξ₁) = k₁₁= 36,

Dξ₂ = cov (ξ₂, ξ₂) = k₂₂= 49,

Dξ₃ = cov (ξ₃, ξ₃) = k₃₃= 36.

2) 

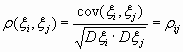
ρ ₁₁ = ρ ₂₂ = ρ ₃₃ = 1 по свойству матрицы коэффициентов корреляции. Т.к. матрица R симметрична относительно главной диагонали, найти надо, к примеру, элементы ρ ₁₂ ; ρ ₂₃ ; ρ ₁₃ :

Тогда матрица коэффициентов корреляции R:

R =