8.2. Квазимонохроматическое приближение

Основная причина, вызывающая изменение формы импульса, движущегося в виде плоской световой волны в пространственно-однородной среде с дисперсией - зависимость скорости распространения света в среде от частоты излучения. Эта зависимость описывается дисперсионной кривой k(). Нелинейность k() приводит к появлению фазовых сдвигов между различными компонентами спектра сигнала по мере его распространения и как следствие, к деформации импульса.

Обычно для математического описания таких явлений применяют аппарат интегралов Фурье. Возможность такого описания следует из линейности волнового уравнения.

Падающий на среду импульс представляют в виде набора плоских монохроматических волн

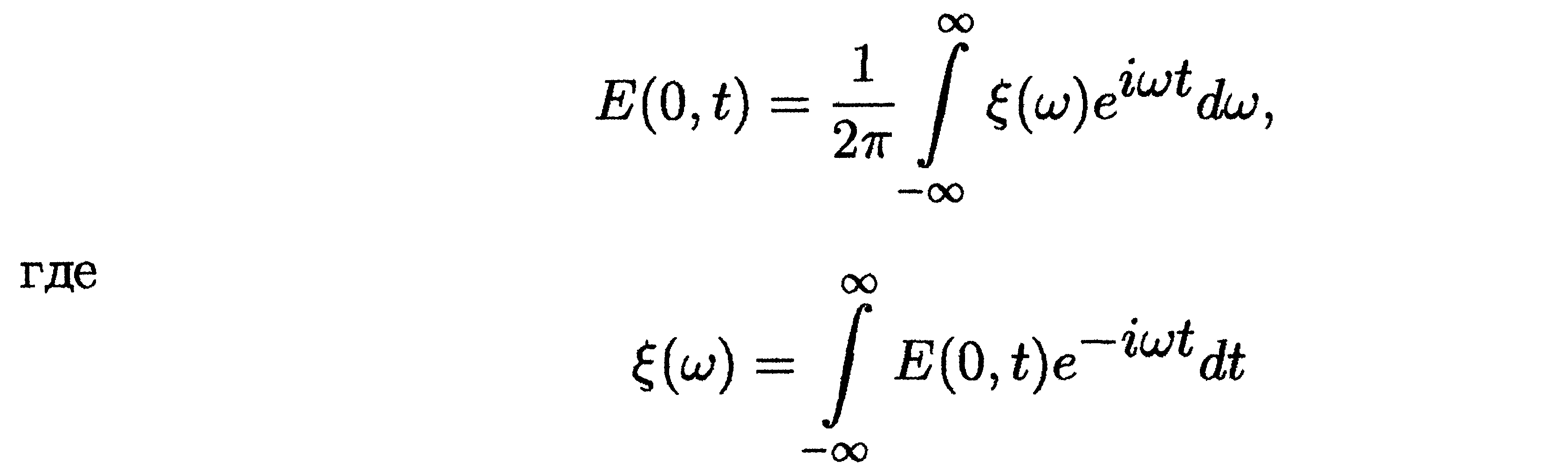
- преобразование Фурье исходного импульса.

Если при распространении в среде импульс не затухает, то амплитуда сигнала после прохождения им расстояния L представляет собой суперпозицию частот, присутствующих во входном импульсе, но с другими фазовыми соотношениями и может быть записана в виде

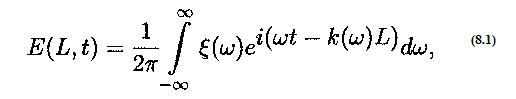
где k() волновое число. При отсутствии потерь - это вещественная функция. Все последующие рассуждения, безусловно, остаются в силе и в том случае, если имеет место затухание или усиление сигнала с коэффициентом поглощения, не зависящим от частоты. Формально это сведётся к добавлению к функции k() чисто мнимой константы, которая может быть без ущерба опущена, так как приводит всего лишь к перенормировке амплитуды результирующего сигнала.

Предположение о пространственной однородности среды позволяет отвлечься от вопросов, связанных с поляризацией излучения, и считать E(L, t) одной из ортогональных проекций вектора напряженности электромагнитного поля. Повсюду в дальнейшем изложении будут рассматриваться только линейно-поляризованные волны, для которых можно ограничиться изложением скалярной теории.

Если дисперсионная кривая среды известна точно, например, измерена с помощью рефрактометра, то применение формулы (8.1) для импульса, спектр которого может быть выражен в аналитическом виде, в принципе, исчерпывает задачу. Известно, однако, лишь несколько модельных случаев, для которых расчёты по формуле (8.1) удалось довести до конца в аналитическом виде. В подавляющем большинстве практически важных случаев явный вид кривой k() неизвестен, поэтому формальное выражение (8.1) оказывается неконструктивным и необходимо искать приближения, которые позволяли бы до конца исследовать конкретные задачи.

Общего рецепта интегрирования (8.1), по-видимому, не существует. Есть, однако, весьма актуальный для практики случай, когда формула (8.1) допускает существенное упрощение. Это случай квазимонохроматических импульсов, Фурье-спектр которых заметно отличен от нуля только в достаточно узкой полосе частот ; вблизи некоторой несущей частоты ₀, то есть при выполнении условия /₀ << 1. Лазерные импульсы, как правило, удовлетворяют этому критерию, поскольку условие генерации в лазере выполняется для сравнительно узкой полосы частот вблизи максимума спектрального контура усиления активной среды. В этом случае интегрирование в формуле (8.1) достаточно провести в узкой полосе частот шириной ; с центром вблизи ω₀, заменив реальную дисперсионную кривую k() другой кривой, хорошо совпадающей с ней в частотном интервале ;. Поскольку при таком подходе аппроксимировать k() надо лишь на небольшом частотном интервале, то лучший способ сделать это состоит в том, чтобы разложить дисперсионную кривую (которая предполагается известной) в ряд по степеням  и удержать в нём несколько первых членов. Коэффициенты разложения, за исключением нулевого, часто называют дисперсионными параметрами первого, второго и т.д. порядков. Таким образом,

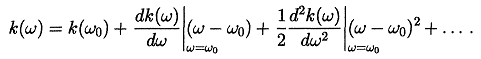(8.2)

В квазимонохроматическом приближении амплитуду световой волны исходного сигнала можно представить в виде произведения медленно меняющейся огибающей f(0,t) и высокочастотного множителя с несущей частотой ₀

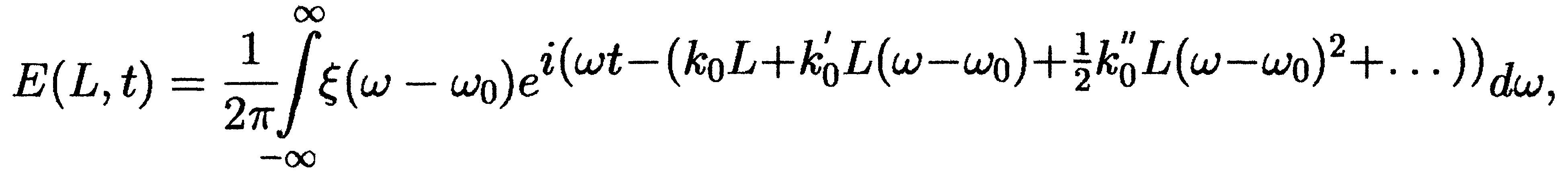
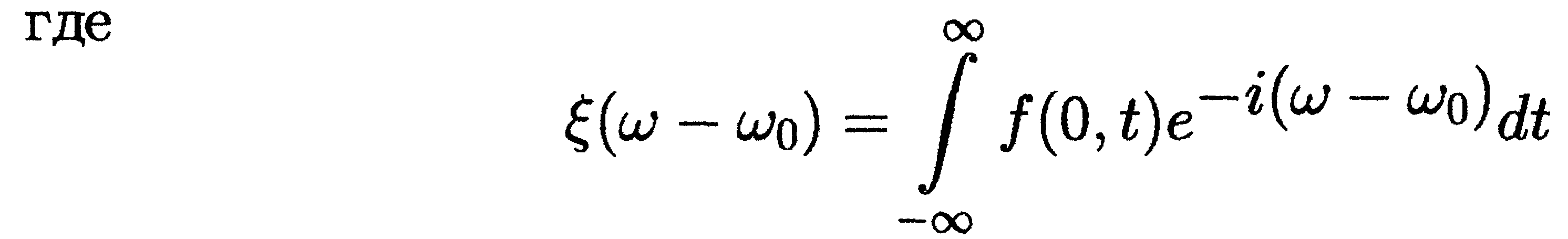
После прохождения в среде расстояния L выражение для амплитуды световой волны примет, с учётом (8.2), следующий вид:

- преобразование Фурье огибающей импульса, а штрихом обозначены производные функции k(), причем индекс 0 означает, что их значения вычислены на частоте ₀.

для которой имеет место следующее интегральное представление:

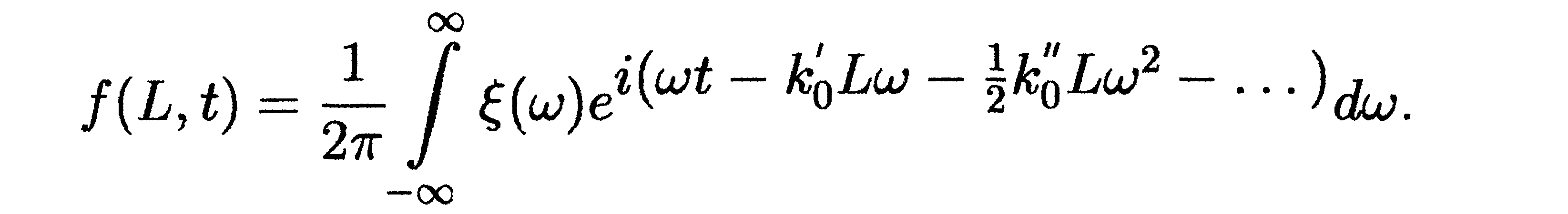
Так же как и для входного сигнала, в выражении для E(L, t) можно выделить высокочастотную часть и медленно меняющийся сомножитель f(L,t) - огибающую импульса

В дальнейшем все изменения формы сигнала удобно будет записывать в «смещённом» времени

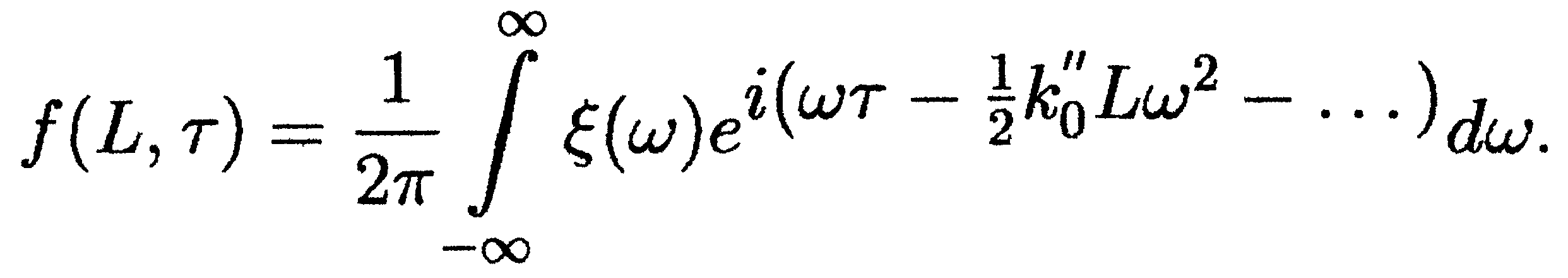
Из малости частотного интервала  следует, что наибольший вклад в деформацию огибающей результирующего сигнала будет вносить первое ненулевое, нелинейное по , слагаемое в разложении (8.2), поэтому и рассматриваемую нами модель часто называют первым неисчезающим приближением теории. В общем случае таким слагаемым будет уже квадратичный по ; член разложения (8.2), что позволяет пренебречь остатком ряда и избавиться от многоточия в показателе экспоненты. При этом нахождение огибающей упрощается до

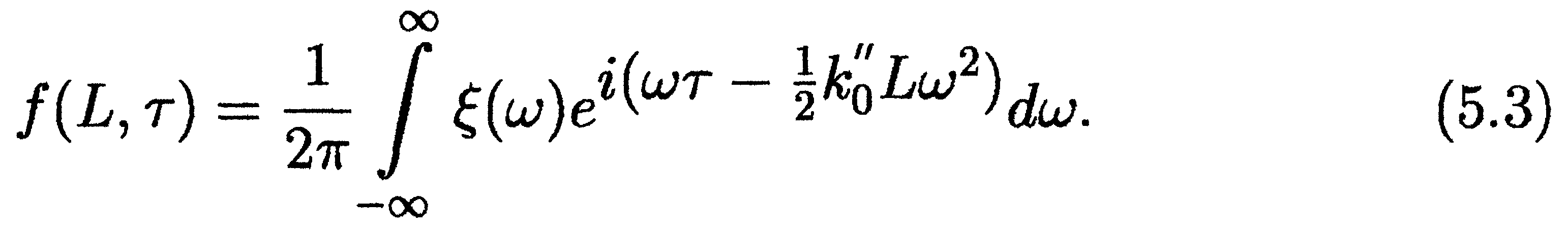
Порядковый номер последнего члена разложения (8.2), который используется для вычисления f(L,), называется порядком квазимонохроматического приближения, что даёт основание называть (8.3) вторым приближением.

Формула (8.3), как правило, и используется в литературе в качестве отправной точки при выполнении практических расчётов деформации лазерных импульсов в диспергирующей среде [1—5]. Из этой формулы видно, что при равенстве нулю k₀^ - второй производной волнового вектора по частоте, никакой деформации импульса в среде не происходит. Временной профиль огибающей на расстоянии L воспроизводит начальный профиль с задержкой t_L. Такая ситуация соответствует случаю линейной зависимости показателя преломления среды от длины волны излучения. Это даёт возможность использовать понятие «групповой скорости», как скорости распространения неискаженной огибающей сигнала в среде с дисперсией .

Для нелинейной дисперсионной кривой параметр будет обычно принимать ненулевые значения, что и приведёт к искажениям огибающей импульса по мере его распространения в среде. При этом понятие «групповая скорость» в определённых ситуациях теряет привычный смысл.