180

Глава 3 основы небесной механики

§ 3.1. Закон всемирного тяготения. Задача двух тел

Основные законы движения тел позволили И. Ньютону сформулировать и математически доказать следующую теорему: “Силы, которыми главные планеты постоянно отклоняются от прямолинейного движения и удерживаются на своих орбитах, направлены к Солнцу и обратно пропорциональны квадратам расстояния от его центра”.

Доказав далее, что сила, удерживающая планеты на их орбитах, тождественна с силой тяжести, действующей на поверхности Земли, Ньютон обобщил эту теорему и выразил ее в форме закона всемирного тяготения:

“Каждые две частицы материи притягивают взаимно друг друга, или тяготеют друг к другу, с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними”.

Математически закон всемирного тяготения Ньютона записывается так:

,

(3.1)

где F — сила притяжения частиц материи, m₁ и m₂ — массы частиц, r — расстояние между ними, G— коэффициент пропорциональности, равный силе, с которой притягиваются друг к другу две частицы с единичными массами и находящиеся на единичном расстоянии друг от друга. Коэффициент G называется постоянной тяготения, или гравитационной постоянной, он равен 6,67 · 10 ^11 Нм² /кг².

Основные закономерности в поступательном движении небесных тел можно установить из исследования задачи двух тел, под которой понимается задача изучения движения этих тел под действием силы взаимного тяготения. При этом тела считаются точечными.

Пусть тела имеют массы m₁ и m₂. Введем прямоугольную декартову систему координат, в которой зададим положение каждого тела радиус-векторами соответственно и . Обозначим через вектор расстояния между телами. Запишем закон динамики для каждого из тел:

,	(3.2)
,	(3.3)

где и — вторые производные векторов.

Отсюда _, но, учитывая, что и обозначив , получим:

.

(3.4)

Уравнение (3.4) описывает движение одного из тел относительно другого тела. Решение этого уравнения получил Ньютон.

Дифференциальное уравнение (3.4) имеет два интеграла движения:

1. Интеграл площадей

,

(3.5)

где — скорость тела. Соотношение (3.5) является следствием закона сохранения момента импульса.

2. Интеграл энергии

.

(3.6)

Соотношение (3.6) является следствием закона сохранения механической энергии.

Основные результаты решения уравнения (3.4) можно представить в виде трех обобщенных законов Кеплера.

§ 3.2. Первый обобщенный закон Кеплера. Характеристические скорости

Законы Кеплера были получены им эмпирически в результате исследования видимых движений планет. Поэтому первый закон Кеплера в формулировке, данной в § 2.2, справедлив лишь в отношении больших планет и тех тел Солнечной системы (некоторых комет, астероидов), которые движутся вокруг Солнца по замкнутым орбитам.

Если же иметь в виду движения небесных тел вообще, то на основании предыдущего параграфа этот закон надо сформулировать в следующем виде: под действием силы притяжения одно небесное тело движется в поле тяготения другого небесного тела по одному из конических сечений — кругу, эллипсу, параболе или гиперболе, при этом другое тело находится в фокусе этого сечения.

В этой формулировке первый обобщенный закон Кеплера будет справедлив уже для всех комет, орбиты которых либо эллипсы, либо параболы, либо гиперболы; он будет справедлив и для спутников больших планет, орбиты которых эллипсы, но в их фокусах находятся большие планеты, и для физических двойных звезд, обращающихся по эллиптическим орбитам вокруг общего центра масс, и т.д.

В общем виде решение уравнения (3.4) имеет вид:

,

(3.7)

где p — фокальный параметр траектории, e — эксцентриситет,  — истинная аномалия, т.е. угол между направлениями на движущееся тело и на ближайшую точку траектории — перицентр.

Величины p и e выражаются через интегралы движения следующим образом:

,	(3.8)
.	(3.9)

Как видно из (3.9), возможны три вида траекторий:

1. если 0  e 1 (h 0) — эллипс (при e = 0 — окружность);

2. если e = 1 (h = 0) — парабола;

3. если e  1 (h  0) — гипербола.

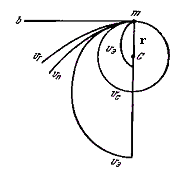
Рис. 3.1. Характеристические скорости.

 

Пусть неподвижное тело массы М, сосредоточенная в точке С, притягивает к себе в некоторый момент материальную точку массы т с силой, обратно пропорциональной квадрату расстояния r между телами (рис. 3.1). В этом случае ускорение точки т будет направлено по прямой тС, а ее дальнейшее движение будет зависеть от расстояния и от величины и направления скорости v₀, которые она имела в начальный момент (в момент начала действия притяжения массой М).

Если скорость v₀ > 0, но не превосходит некоторого предела , то точка т будет двигаться по эллипсу, в одном из фокусов которого будет находиться точка С. Плоскость эллипса будет проходить через точки С, т и направление скорости v₀ .

Форма и размеры эллипса будут различны, смотря по величине скорости v₀ . При малых v₀ эллипс будет сильно сжатым, его большая ось будет лишь немного больше, чем Cm, и точка С будет находиться в фокусе, далеком от m. Если скорость v₀ будет близка к скорости v_c , но меньше ее, то эксцентриситет эллипса будет мал, его большая полуось будет лишь немного меньше, чем Cm, точка С приблизится к центру эллипса, но останется в фокусе, далеком от т.

Если начальная скорость v₀ = v_c и будет направлена перпендикулярно к линии Cm, то точка m будет двигаться по кругу радиуса Сm.

Если v₀ > v_c , но не превосходит некоторого предела , то точка т будет двигаться по эллипсу, но точка С при этом будет находиться в фокусе, близком к m, а большая ось эллипса будет тем больше, чем ближе v₀ к .

Если v₀ = , то точка т будет двигаться по параболе, обе ветви которой уходят в бесконечность, приближаясь к направлению, параллельному оси Ст. По мере того как точка т будет удаляться от тела М, ее скорость будет стремиться к нулю.

Если v₀ > , то точка т будет двигаться по гиперболе, ветви которой уходят в бесконечность и, при очень большой начальной скорости, приближаются к направлению, перпендикулярному к оси Ст. По мере того как точка т будет удаляться по гиперболе, ее скорость будет стремиться к некоторой постоянной величине.

Наконец, в предельных случаях, когда v₀ = , точка т будет двигаться по прямой тb, а когда v₀ = =0, то по прямой тС.

Можно показать, что скорость v точки т на любом расстоянии r от точки С получается из формулы

,

(3.10)

где а — большая полуось траектории.

Скорость v_c называется 1-й характеристической или циклической (круговой) скоростью, а — 2-й характеристической или параболической скоростью. Скорость эллиптического движения v_э заключена в пределах 0 < v_э < , а гиперболическая скорость v_r > .

Если рассматривать движение искусственного спутника вблизи поверхности Земли, то 1-я характеристическая скорость называется 1-й космической скоростью и равна 7,9 кмс, а 2-я характеристическая скорость — 2-й космической, равной 11,2 кмс.
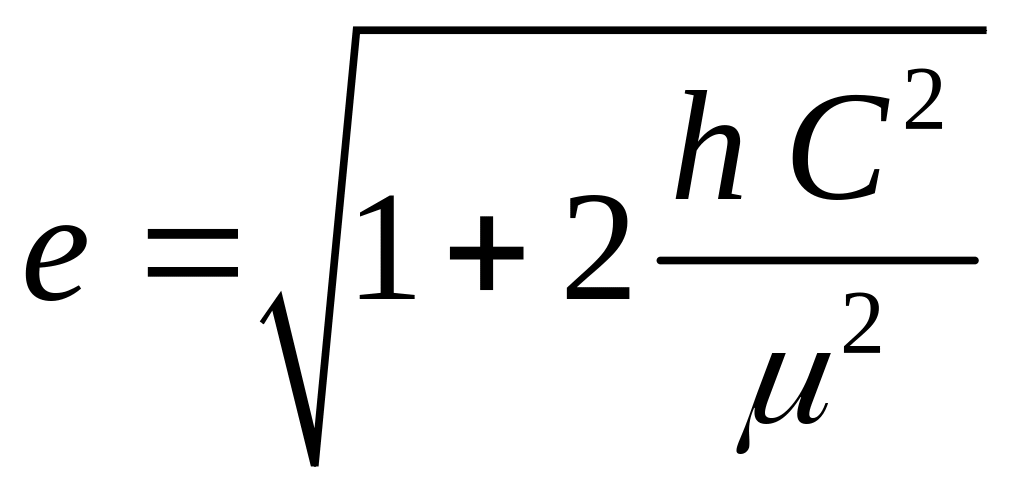