14. Частичные пределы. Верхний и нижний пределы.

Число (или символ  или ) называется частичным пределом последовательности , если оно (он) является пределом некоторой ее подпоследовательности.

Наибольший (соотв, наименьший) из частичных пределов ограниченной последовательности называется верхним (соотв., нижним) ее пределом

15. Фундаментальные последовательности. Критерий Коши сходимости числовой последовательности.

Последовательность, удовлетворяющая критерию сходимости Коши, называется фундаментальной.

Критерий Коши. Пусть задана числовая последовательность {x_n}. Эта последовательность сходится тогда и только тогда, когда для любого числа ε > 0 существует номер N такой, что при всех n > N  и любых натуральных m выполняется неравенство 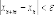 (т.е. расстояние между членами последовательности с номерами n  и n+m меньшеε).

16. Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности.

17. Критерий Коши существования предела функции.

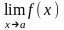Теорема (критерий Коши). Пусть функция определена на множестве и (конечная или бесконечная) точка сгущения этого множества. Для того, чтобы существовал предел ₍₁₎

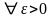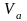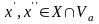
необходимо и достаточно, чтобы существовала такая окрестность точки , что для любых 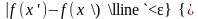. (2)

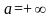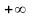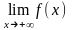Замечание 1. Если в этой теореме , то в терминах неравенств теорема может быть сформулирована следующим образом: Пусть функция определена на множестве и точка – точка сгущения этого множества . Для того, чтобы существовал предел (1’)

необходимо и достаточно, чтобы существовало такое , что . (2’) для любых 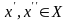таких, что .

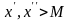18. Локальные свойства функций имеющих предел.

Определение 1. Пусть функция определена на множестве и 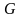– некоторое его подмножество ( 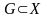). Говорят, что функция ограничена (соотв., ограничена сверху или снизу) на множестве , если его образ 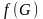есть ограниченное (соотв., ограниченное сверху или снизу) множество.

Теорема 1 (о локальной ограниченности). Пусть функция определена на множестве и - точка сгущения этого множества. Тогда если существует предел , то существует такая окрестность точки , что функция ограничена на множестве .Ниже знак числа обозначается через .

Теорема 2 (о стабилизации знака). Пусть функция определена на множестве и - точка сгущения этого множества. Тогда если существует отличный от нуля предел 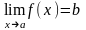, то в некоторой проколотой окрестности точки функция имеет тот же знак, что и этот предел: точнее, существует такая окрестность точки , что

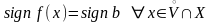
19. Теорема о пределе суперпозиции.

Теорема. Пусть функция определена на множестве , – точка сгущения множества и существует предел 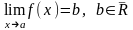(1)

Пусть, кроме того, функция определена на множестве , 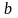– точка сгущения множества и существует предел 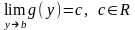. (2)

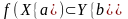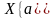Тогда, если , (3) то на множестве имеет смысл суперпозиция 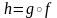и существует предел 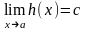. (4)

Замечание 1. Равенство (4) с учетом определения суперпозиции функций можно записать так: .

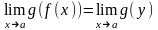Таким образом, теорема 1 указывает условия, при выполнении которых под знаком предела справа в этом равенстве можно сделать замену переменной по правилу 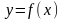, при этом зная этот предел, мы знаем и предел, стоящий слева в этом равенстве.

Замечание 2. Если – область значений функции и либо 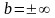, либо эта функция является строго монотонной, то условие (3) теоремы 1 заведомо выполняется. На практике именно проверка условия (3) является "камнем преткновения" для использования этой теоремы.

Д о к а з а т е л ь с т в о. Выберем произвольную окрестность 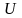точки 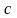. Тогда, в силу равенства (2), найдется окрестность 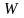точки такая, что 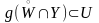(5). В свою очередь, в силу равенства (1), для окрестности точки найдется такая окрестность точки , что 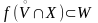, а так как 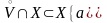и по условию , то отсюда следует, что 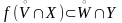(6)

Из включений (5) и (6) следует, что .

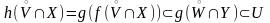Таким образом, для произвольно выбранной окрестности точки нашлась такая окрестность точки , что 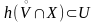. По определению предела это и означает, что имеет место равенство (4) □