
- •Множества и действия над ними.
- •Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
- •Сюрьективные, инъективные и биективные отображения. Обратное отображение.
- •Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
- •Предел числовой последовательности. Сходящиеся и расходящиеся последовательности.
- •Арифметические свойства сходящихся последовательностей.
- •Предельный переход в неравенствах (для последовательностей).
- •Монотонные последовательности. Теорема о пределе монотонной последовательности.
- •Применение теоремы о пределе монотонной последовательности к вычислению пределов.
- •Число e.
- •Бесконечно малые и бесконечно большие последовательности.
- •Лемма о вложенных отрезках.
- •Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
- •Частичные пределы. Верхний и нижний пределы.
- •Фундаментальные последовательности. Критерий Коши сходимости числовой последовательности.
- •Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности.
- •Критерий Коши существования предела функции.
- •Локальные свойства функций имеющих предел.
- •Теорема о пределе суперпозиции.
- •Односторонние пределы.
- •Бесконечные пределы и пределы в бесконечности.
- •Бесконечно малые и бесконечно большие функции.
- •Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
- •Замечательные пределы
- •Асимптоты графика функции
- •Понятие непрерывной функции. Простейшие свойства непрерывных функций, в том числе, вытекающие из свойств предела.
- •Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры
- •Равномерно непрерывные функции. Теорема Кантора.
- •Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.
- •Теоремы Вейерштрасса о непрерывных на отрезке функциях.
- •Критерий непрерывности монотонной функции. Теорема об обратной функции к непрерывной и строго монотонной функции.
- •Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции в данной точке.
- •Дифференцируемые функции. Понятие дифференциала.
- •Арифметические операции с дифференцируемыми функциями.
- •Дифференцирование сложной функции.
- •Дифференцирование обратной функции.
- •Дифференцирование элементарных функций. Таблица производных.
- •Локальный экстремум функции. Теорема Ферма.
- •Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
- •Производные и дифференциалы высших порядков.
- •Формула Тейлора для многочлена.
- •Локальная формула Тейлора (формула Тейлора с остаточным членом в форме Пеано).
- •Формула Тейлора с остаточным членом в форме Лагранжа и в форме Коши.
- •Разложение элементарных функций по формуле Тейлора.
- •Правило Лопиталя.
- •Условия монотонности функции.
- •Условия экстремума функции.
- •Условия выпуклости функции.
- •Д о к а з а т е л ь с т в о. Необходимость. Пусть функция является выпуклой. Выберем произвольно , , и покажем, что (9)
- •Точки перегиба графика функции.
- •Множество вещественных чисел (натуральные, целые, рациональные и иррациональные числа, модуль (абсолютная величина вещественного числа) и его свойства.
- •Комплексные числа.
Дифференцируемые функции. Понятие дифференциала.
Пусть функция определена в окрестности точки .
Определение
1. Если существует такая линейная
функция
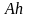 вещественного аргумента
(
вещественного аргумента
(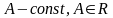 ),
что приращение
),
что приращение
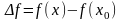 функции
может быть представлено в виде
функции
может быть представлено в виде
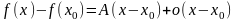 (1), где
(1), где
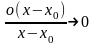 при
при
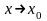 ,
то функция
называется дифференцируемой в точке
,
а соответствующая линейная функция
аргумента
,
то функция
называется дифференцируемой в точке
,
а соответствующая линейная функция
аргумента
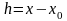 называется
ее дифференциалом в этой точке.
называется
ее дифференциалом в этой точке.
Дифференциал
функции
в точке
обычно обозначается одним из символов:
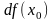 или
или
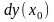 .
.
В
последнем случае имеют в виду, что
,
при этом часто опускают указание о том,
в какой точке рассматривается этот
дифференциал, т.е. для обозначения
дифференциала используют символы
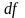 или
или
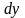 .
Таким образом,
.
Таким образом,
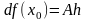 (2).
(2).
Замечание
1. Очевидно, равенство (1) можно записать
в виде
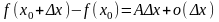 (1’), где
и
(1’), где
и
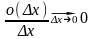 ,
(т.е.
,
(т.е.
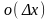 - бесконечно малая при
- бесконечно малая при
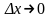 высшего порядка по сравнению с
)
или, короче, в виде
высшего порядка по сравнению с
)
или, короче, в виде
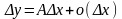 (1’’), где
(1’’), где
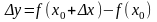 - приращение функции в точке
,
соответствующее приращению аргумента
.
- приращение функции в точке
,
соответствующее приращению аргумента
.
Замечание
2. Поскольку
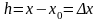 ,
то вместо (2) также пишут:
,
то вместо (2) также пишут:
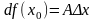 (2’)
(2’)
Теорема 1. Для того, чтобы функция была дифференцируемой в точке , необходимо и достаточно, чтобы она имела в этой точке конечную производную .
Д
о к а з а т е л ь с т в о. Необходимость.
Пусть функция
дифференцируема в точке
.
Тогда из равенства (1) следует, что
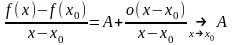
Это
означает, что существует конечная
производная
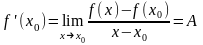 .
.
Достаточность.
Предположим, что в точке
функция
имеет конечную производную
.
Тогда из равенства
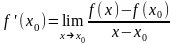 следует, что
следует, что
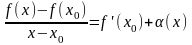 (3), где
(3), где
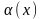 - бесконечно малая при
функция. Поэтому
- бесконечно малая при
функция. Поэтому
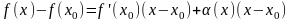 (4) и так как
(4) и так как
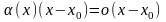 (ибо
(ибо
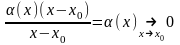 ),
то равенство (4) можно записать в
виде:
),
то равенство (4) можно записать в
виде:
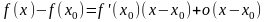 (5) в виде (1), где
(5) в виде (1), где
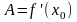 .
Таким образом, функция
дифференцируема в точке
□
.
Таким образом, функция
дифференцируема в точке
□
Замечание
3. Из доказательства теоремы видно,
что дифференциал функции в точке
есть следующая линейная функция от
приращения аргумента
:
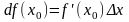 (6). А поскольку для функции
(6). А поскольку для функции
 имеем
имеем
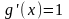 , то
, то
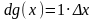 ,
т.е.
,
т.е.
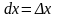 ,
,
Таким
образом, можно сказать, что
- дифференциал
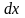 независимой переменной
и, следовательно, определению дифференциала
можно придать форму:
независимой переменной
и, следовательно, определению дифференциала
можно придать форму:
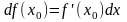 .
(7)
.
(7)
Отсюда, в частности, становится понятным, почему производную обозначают также .
Арифметические операции с дифференцируемыми функциями.
Теорема.
Пусть функции
и
определены в окрестности точки
и дифференцируемы в этой точке. Тогда
в этой точке дифференцируема и каждая
из функций
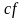
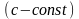 ,
,
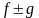 ,
,
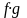 и
и
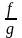 (при
(при
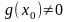 ),
причем
),
причем
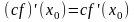 (1),
(1),
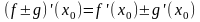 (2),
(2),
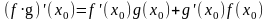 (3),
(3),
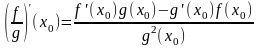 (4).
(4).
Д
о к а з а т е л ь с т в о. 1.
Дифференцируемость
функции
и равенство
(1) очевидно
будут установлены, если будут установлены
дифференцируемость функции
и равенство (3). В этом случае достаточно
будет рассмотреть функцию
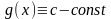 .
.
2.
Дифференцируемость
функции
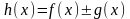 и равенство
(2) вытекают из того, что имеют место
равенства
и равенство
(2) вытекают из того, что имеют место
равенства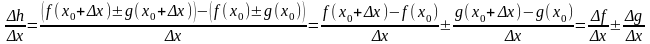 и
из того, что по условию существуют
конечные пределы
и
из того, что по условию существуют
конечные пределы
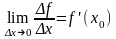 и
и
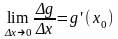 ,
при этом
следует помнить, что дифференцируемость
функции в точке
равносильна существованию конечной ее
производной в этой точке.
,
при этом
следует помнить, что дифференцируемость
функции в точке
равносильна существованию конечной ее
производной в этой точке.
3. Дифференцируемость произведения функций и равенство (3).
Пусть
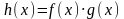 .
Тогда
.
Тогда
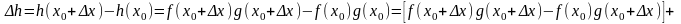
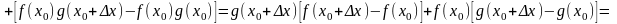
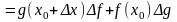 ,
и, следовательно,
,
и, следовательно,
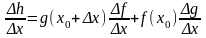 (5).
(5).
В
силу дифференцируемости функций
и
в точке
,
существуют конечные пределы
,
и
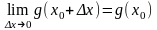 (6). Поэтому из (5) следует, что существует
конечный предел
(6). Поэтому из (5) следует, что существует
конечный предел
 (7), т.е. функция
(7), т.е. функция
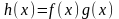 дифференцируема в точке
.
Переходя в равенстве (5) к пределу при
с учетом равенств (6) и (7) получим равенство
(3).
дифференцируема в точке
.
Переходя в равенстве (5) к пределу при
с учетом равенств (6) и (7) получим равенство
(3).
4.
Дифференцируемость
и равенство
(4). Положим
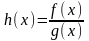 .
По крайней мере, в некоторой окрестности
точки
,
это определение корректно, так как
и функция
непрерывна в точке
.
.
По крайней мере, в некоторой окрестности
точки
,
это определение корректно, так как
и функция
непрерывна в точке
.
Далее,
имеем:

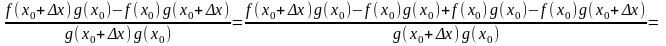
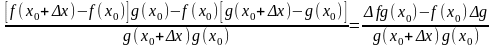 ,
и, следовательно,
,
и, следовательно,
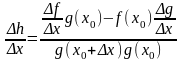 .
.
Рассуждая
теперь аналогично пункту 3 данного
доказательства, убеждаемся, что функция
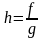 дифференцируема в точке
,
а переходя здесь к пределу при
получим также и равенство (4) □
дифференцируема в точке
,
а переходя здесь к пределу при
получим также и равенство (4) □
Замечание
(о формулах для дифференциалов, вытекающих
из формул (1) - (6)). Учитывая, что дифференциал
функции
в точке
находится по правилу
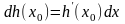 из формул (1)–(4) , умножая каждую из них
на
,
получим следующие формулы для
дифференциалов:
из формул (1)–(4) , умножая каждую из них
на
,
получим следующие формулы для
дифференциалов:
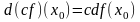 ,
(здесь
,
(здесь
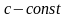 );
);
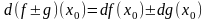 ;
;
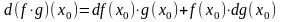 ;
;
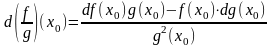 .
.
