
- •Множества и действия над ними.
- •Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
- •Сюрьективные, инъективные и биективные отображения. Обратное отображение.
- •Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
- •Предел числовой последовательности. Сходящиеся и расходящиеся последовательности.
- •Арифметические свойства сходящихся последовательностей.
- •Предельный переход в неравенствах (для последовательностей).
- •Монотонные последовательности. Теорема о пределе монотонной последовательности.
- •Применение теоремы о пределе монотонной последовательности к вычислению пределов.
- •Число e.
- •Бесконечно малые и бесконечно большие последовательности.
- •Лемма о вложенных отрезках.
- •Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
- •Частичные пределы. Верхний и нижний пределы.
- •Фундаментальные последовательности. Критерий Коши сходимости числовой последовательности.
- •Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности.
- •Критерий Коши существования предела функции.
- •Локальные свойства функций имеющих предел.
- •Теорема о пределе суперпозиции.
- •Односторонние пределы.
- •Бесконечные пределы и пределы в бесконечности.
- •Бесконечно малые и бесконечно большие функции.
- •Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
- •Замечательные пределы
- •Асимптоты графика функции
- •Понятие непрерывной функции. Простейшие свойства непрерывных функций, в том числе, вытекающие из свойств предела.
- •Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры
- •Равномерно непрерывные функции. Теорема Кантора.
- •Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.
- •Теоремы Вейерштрасса о непрерывных на отрезке функциях.
- •Критерий непрерывности монотонной функции. Теорема об обратной функции к непрерывной и строго монотонной функции.
- •Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции в данной точке.
- •Дифференцируемые функции. Понятие дифференциала.
- •Арифметические операции с дифференцируемыми функциями.
- •Дифференцирование сложной функции.
- •Дифференцирование обратной функции.
- •Дифференцирование элементарных функций. Таблица производных.
- •Локальный экстремум функции. Теорема Ферма.
- •Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
- •Производные и дифференциалы высших порядков.
- •Формула Тейлора для многочлена.
- •Локальная формула Тейлора (формула Тейлора с остаточным членом в форме Пеано).
- •Формула Тейлора с остаточным членом в форме Лагранжа и в форме Коши.
- •Разложение элементарных функций по формуле Тейлора.
- •Правило Лопиталя.
- •Условия монотонности функции.
- •Условия экстремума функции.
- •Условия выпуклости функции.
- •Д о к а з а т е л ь с т в о. Необходимость. Пусть функция является выпуклой. Выберем произвольно , , и покажем, что (9)
- •Точки перегиба графика функции.
- •Множество вещественных чисел (натуральные, целые, рациональные и иррациональные числа, модуль (абсолютная величина вещественного числа) и его свойства.
- •Комплексные числа.
Дифференцирование сложной функции.
(суперпозицию двух и более функций мы называем также сложной функцией)
Теорема.
Пусть
функция
определена на интервале
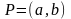 ,
а функция
определена на интервале
,
а функция
определена на интервале
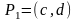 ,
причем
,
причем
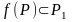 .
Тогда если функция
дифференцируема в точке
.
Тогда если функция
дифференцируема в точке
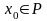 ,
а функция
дифференцируема в точке
,
а функция
дифференцируема в точке
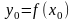 ,
то сложная функция
дифференцируема в точке
и
,
то сложная функция
дифференцируема в точке
и
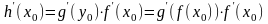 (1)
(1)
Д
о к а з а т е л ь с т в о. В силу
дифференцируемости функций
и
,
соответственно, в точках
и
 ,
имеем
,
имеем
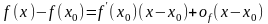 ;
;
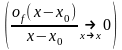 (2), и
(2), и
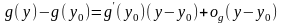 ;
;
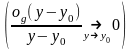 (3). Как известно
(3). Как известно
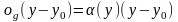 (4), где
(4), где
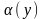 - бесконечно малая при
- бесконечно малая при
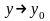 ,
причем без ущерба для общности можно
считать, что
,
причем без ущерба для общности можно
считать, что
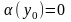 ,
то есть можно считать, что функция
непрерывна в точке
.
Из (3) и (4) следует, что
,
то есть можно считать, что функция
непрерывна в точке
.
Из (3) и (4) следует, что
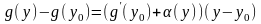 .
Подставляя сюда
,
и используя затем равенство (2), получим
.
Подставляя сюда
,
и используя затем равенство (2), получим
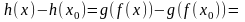
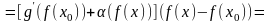
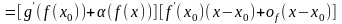 и, следовательно,
и, следовательно,
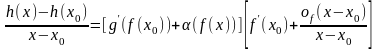 (5).
(5).
Поскольку
функция
непрерывна в точке
,
а функция
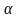 непрерывна в точке
и
,
то по теореме о непрерывности сложной
функции
непрерывна в точке
и
,
то по теореме о непрерывности сложной
функции
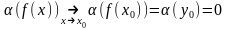 .
.
А
так как, кроме того,
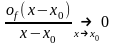 ,
то из (5) следует, что существует конечная
производная
,
то из (5) следует, что существует конечная
производная
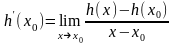 и имеет место равенство (1). Для завершения
доказательства теоремы остается
вспомнить, что существование конечной
производной
и имеет место равенство (1). Для завершения
доказательства теоремы остается
вспомнить, что существование конечной
производной
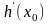 равносильно дифференцируемости функции
в точке
равносильно дифференцируемости функции
в точке
Замечание.
Пусть выполнены условия теоремы. Тогда
по определению дифференциала
(6), и, в силу равенства (1), для сложной
функции будем иметь
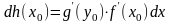 или
или
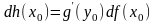 (7).
(7).
Считая
точку
произвольной (то есть заменяя
на произвольное
).
Равенства (6) и (7) записывают в виде
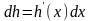 (6¢),
(6¢),
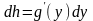 (7¢).
(7¢).
Эти формулы показывают, что формально вид дифференциала не меняется как при записи его через независимую переменную , так и при записи через зависимую переменную . В этом состоит, так называемое, свойство инвариантности дифференциала, который называют также первым дифференциалом.
Дифференцирование обратной функции.
no1. Теорема об обратной функции к непрерывной строго монотонной функции.
Прежне
всего напомним, что по
следствию из второй теоремы Больцано-Коши
если
функция
определена
и непрерывна на конечном или бесконечном
промежутке
,
то множество
ее значений
также есть
промежуток
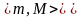 ,
где
.
,
где
.
Это утверждение дополняет следствие из второй теоремы Вейерштрасса:
Множество
значений непрерывной на отрезке
функции
является отрезком
,
где
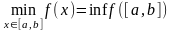 ,
,
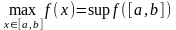 .
.
В свою очередь, последнее утверждение дополняет следующая Теорема 1 (критерий непрерывности монотонной функции). Для того, чтобы монотонная на отрезке функция была непрерывной на нем, необходимо и достаточно, чтобы множество ее значений было отрезком.
Напомним также, что справедлива следующая важная Теорема 2 (об обратной функции к непрерывной, строго монотонной). Пусть функция непрерывна и строго монотонна на отрезке . Тогда существует обратная к ней функция , которая является непрерывной и строго монотонной в том же смысле, что и функция .
Следствие. Пусть функция непрерывна и строго монотонна на произвольном промежутке . Тогда обратная к ней функция непрерывна и строго монотонна (в том же смысле что и функция ) на промежутке .
no1. Теорема о дифференцировании обратной
Теорема
3.
Пусть функция
строго монотонна и непрерывна в
окрестности
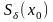 точки
.
Пусть, кроме
того, функция
дифференцируема в точке
и
точки
.
Пусть, кроме
того, функция
дифференцируема в точке
и
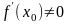 .
Тогда обратная к ней функция
дифференцируема в точке
,
причем
.
Тогда обратная к ней функция
дифференцируема в точке
,
причем
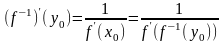 (1)
(1)
Д
о к а з а т е л ь с т в о. Из условий теоремы
следует, что существует конечный,
отличный от нуля предел
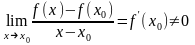 .
Тогда по теореме о пределе частного
существует конечный предел
.
Тогда по теореме о пределе частного
существует конечный предел
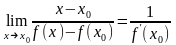 (2). Рассмотрим функцию
(2). Рассмотрим функцию
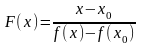 (3).
(3).
В
силу строгой монотонности функции
она определена в проколотой окрестности
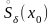 точки
.
В точке
функция
точки
.
В точке
функция
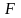 имеет конечный предел (2). Поэтому если
доопределить ее в этой точке равенством
имеет конечный предел (2). Поэтому если
доопределить ее в этой точке равенством
 ,
,
то
она будет непрерывной в этой точке.
Тогда учитывая, что функция
непрерывна в точке
(как обратная к непрерывной, строго
монотонной функции
),
по теореме о непрерывности суперпозиции
заключаем, что сложная функция
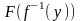 будет непрерывной в той же точке
и, следовательно,
будет непрерывной в той же точке
и, следовательно,
 (4).
(4).
Но
в силу (3) в некоторой проколотой
окрестности
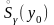 точки
имеет место равенство
точки
имеет место равенство
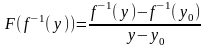 .
Поэтому из (4) следует, что функция
дифференцируема в точке
и имеют место равенства (1) □
.
Поэтому из (4) следует, что функция
дифференцируема в точке
и имеют место равенства (1) □
