
- •Множества и действия над ними.
- •Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
- •Сюрьективные, инъективные и биективные отображения. Обратное отображение.
- •Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
- •Предел числовой последовательности. Сходящиеся и расходящиеся последовательности.
- •Арифметические свойства сходящихся последовательностей.
- •Предельный переход в неравенствах (для последовательностей).
- •Монотонные последовательности. Теорема о пределе монотонной последовательности.
- •Применение теоремы о пределе монотонной последовательности к вычислению пределов.
- •Число e.
- •Бесконечно малые и бесконечно большие последовательности.
- •Лемма о вложенных отрезках.
- •Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
- •Частичные пределы. Верхний и нижний пределы.
- •Фундаментальные последовательности. Критерий Коши сходимости числовой последовательности.
- •Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности.
- •Критерий Коши существования предела функции.
- •Локальные свойства функций имеющих предел.
- •Теорема о пределе суперпозиции.
- •Односторонние пределы.
- •Бесконечные пределы и пределы в бесконечности.
- •Бесконечно малые и бесконечно большие функции.
- •Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
- •Замечательные пределы
- •Асимптоты графика функции
- •Понятие непрерывной функции. Простейшие свойства непрерывных функций, в том числе, вытекающие из свойств предела.
- •Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры
- •Равномерно непрерывные функции. Теорема Кантора.
- •Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.
- •Теоремы Вейерштрасса о непрерывных на отрезке функциях.
- •Критерий непрерывности монотонной функции. Теорема об обратной функции к непрерывной и строго монотонной функции.
- •Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции в данной точке.
- •Дифференцируемые функции. Понятие дифференциала.
- •Арифметические операции с дифференцируемыми функциями.
- •Дифференцирование сложной функции.
- •Дифференцирование обратной функции.
- •Дифференцирование элементарных функций. Таблица производных.
- •Локальный экстремум функции. Теорема Ферма.
- •Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
- •Производные и дифференциалы высших порядков.
- •Формула Тейлора для многочлена.
- •Локальная формула Тейлора (формула Тейлора с остаточным членом в форме Пеано).
- •Формула Тейлора с остаточным членом в форме Лагранжа и в форме Коши.
- •Разложение элементарных функций по формуле Тейлора.
- •Правило Лопиталя.
- •Условия монотонности функции.
- •Условия экстремума функции.
- •Условия выпуклости функции.
- •Д о к а з а т е л ь с т в о. Необходимость. Пусть функция является выпуклой. Выберем произвольно , , и покажем, что (9)
- •Точки перегиба графика функции.
- •Множество вещественных чисел (натуральные, целые, рациональные и иррациональные числа, модуль (абсолютная величина вещественного числа) и его свойства.
- •Комплексные числа.
Число e.
Предположим,
что в некотором банке годовая процентная
ставка равняется 100%. Такие ставки по
банковским вкладам действительно были
в России в первой половине 90-х годов
минувшего столетия. Далее предположим,
что если вклад пролежал на счете a
дней, то банк
начисляет за этот срок проценты по
вкладу в размере
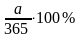 ,
т. е. пропорционально сроку вклада,
исходя из годовой ставки 100% (для простоты
считаем, что в году 365 дней). Попытаемся
выяснить, можно ли при указанных условиях
вклада получить больше 100% годовых?
,
т. е. пропорционально сроку вклада,
исходя из годовой ставки 100% (для простоты
считаем, что в году 365 дней). Попытаемся
выяснить, можно ли при указанных условиях
вклада получить больше 100% годовых?
Если мы поместим одну денежную единицу (скажем, 1 тысячу рублей) на полгода, то, сняв вклад в размере 1,5 (полутора) единиц через полгода и положив сразу же их в тот же банк, в конце года мы получим уже
(1 + 0.5)(1 + 0.5) = 2.25 единиц
то есть получим 125% годовых, что больше чем установленная банком годовая ставка.
Нетрудно
понять, что если мы в течение года будем
n
раз
переоформлять вклад через равные периоды
времени, то положив одну единицу в начале
года, в конце года мы получим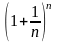 единиц, т. е. получим
единиц, т. е. получим
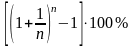 годовых. Очевидно, что при любом
натуральном n,
мы таким образом получим больше 100%
годовых. Поэтому банки начисляют проценты
по вкладам – речь идет о вкладах под
простые проценты, – пролежавшим меньше
года по специальным правилам, а именно,
так, что реальная годовая ставка при
указанной выше процедуре n
– кратного «снятия – вложения» вклада
не превышает установленной ими годовой
ставки (в нашем случае рассматривалась
ставка 100%).
годовых. Очевидно, что при любом
натуральном n,
мы таким образом получим больше 100%
годовых. Поэтому банки начисляют проценты
по вкладам – речь идет о вкладах под
простые проценты, – пролежавшим меньше
года по специальным правилам, а именно,
так, что реальная годовая ставка при
указанной выше процедуре n
– кратного «снятия – вложения» вклада
не превышает установленной ими годовой
ставки (в нашем случае рассматривалась
ставка 100%).
«Существует
ли предел последовательности
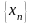 ,
,
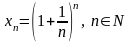 и если существует, то чему равен этот
предел»? Для того, чтобы дать ответ нам
этот вопрос понадобится следующая
лемма:
и если существует, то чему равен этот
предел»? Для того, чтобы дать ответ нам
этот вопрос понадобится следующая
лемма:
Лемма
1. Для
любого
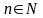 и любого
и любого
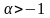 справедливо неравенство
справедливо неравенство (1)
Д о к
а з а т е л ь с т в о.
Проведем его по индукции. При n
= 1 неравенство
(1), очевидно, выполняется как равенство
(вообще при любом
(1)
Д о к
а з а т е л ь с т в о.
Проведем его по индукции. При n
= 1 неравенство
(1), очевидно, выполняется как равенство
(вообще при любом
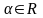 ).
Предположим,
что оно справедливо при
n
= k,
т.е. предположим, что
).
Предположим,
что оно справедливо при
n
= k,
т.е. предположим, что
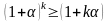 .
Тогда
.
Тогда
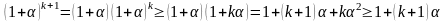 ,
т.е. оно
справедливо и при n
= k
+ 1. Таким
образом, в соответствии с методом
математической индукции неравенство
(1) верно
.
,
т.е. оно
справедливо и при n
= k
+ 1. Таким
образом, в соответствии с методом
математической индукции неравенство
(1) верно
.
Замечание 1. Обратите внимание на то, где мы при доказательстве воспользовались условием, что .
Лемма
2. Существует
предел
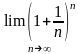 .
.
Д
о к а з а т е л ь с т в о.
Рассмотрим сначала последовательность
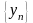 ,
,
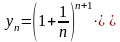 Используя неравенство
Бернулли,
при
Используя неравенство
Бернулли,
при
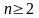 будем
иметь:
будем
иметь:
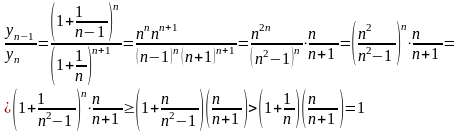
Таким
образом,
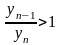 и следовательно
и следовательно
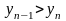 ,
то есть последовательность
- убывающая.
,
то есть последовательность
- убывающая.
Кроме
того, очевидно, что последовательность
положительная
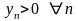 .
Следовательно, она ограничена снизу.
Поэтому существует предел
.
Следовательно, она ограничена снизу.
Поэтому существует предел
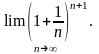 Возвращаясь к интересующей нас
последовательности
,
Возвращаясь к интересующей нас
последовательности
,
 ,
видим, что
,
видим, что
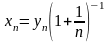 .
Поскольку существуют пределы:
.
Поскольку существуют пределы:
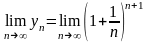 и
и
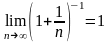 ,
то по теореме о пределе произведения
последовательностей существует и предел
,
то по теореме о пределе произведения
последовательностей существует и предел
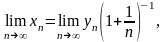 т.е.
предел
т.е.
предел
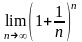 ■
■
Замечание 2. Этот предел обозначают буквой e и называют числом e. Можно доказать, что число e иррациональное. В настоящее время оно вычислено с большей степени точности в частности, в пределах первых пятнадцати знаков после запятой
e = 2,718281828459045…
