
- •Множества и действия над ними.
- •Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
- •Сюрьективные, инъективные и биективные отображения. Обратное отображение.
- •Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
- •Предел числовой последовательности. Сходящиеся и расходящиеся последовательности.
- •Арифметические свойства сходящихся последовательностей.
- •Предельный переход в неравенствах (для последовательностей).
- •Монотонные последовательности. Теорема о пределе монотонной последовательности.
- •Применение теоремы о пределе монотонной последовательности к вычислению пределов.
- •Число e.
- •Бесконечно малые и бесконечно большие последовательности.
- •Лемма о вложенных отрезках.
- •Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
- •Частичные пределы. Верхний и нижний пределы.
- •Фундаментальные последовательности. Критерий Коши сходимости числовой последовательности.
- •Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности.
- •Критерий Коши существования предела функции.
- •Локальные свойства функций имеющих предел.
- •Теорема о пределе суперпозиции.
- •Односторонние пределы.
- •Бесконечные пределы и пределы в бесконечности.
- •Бесконечно малые и бесконечно большие функции.
- •Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
- •Замечательные пределы
- •Асимптоты графика функции
- •Понятие непрерывной функции. Простейшие свойства непрерывных функций, в том числе, вытекающие из свойств предела.
- •Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры
- •Равномерно непрерывные функции. Теорема Кантора.
- •Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.
- •Теоремы Вейерштрасса о непрерывных на отрезке функциях.
- •Критерий непрерывности монотонной функции. Теорема об обратной функции к непрерывной и строго монотонной функции.
- •Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции в данной точке.
- •Дифференцируемые функции. Понятие дифференциала.
- •Арифметические операции с дифференцируемыми функциями.
- •Дифференцирование сложной функции.
- •Дифференцирование обратной функции.
- •Дифференцирование элементарных функций. Таблица производных.
- •Локальный экстремум функции. Теорема Ферма.
- •Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
- •Производные и дифференциалы высших порядков.
- •Формула Тейлора для многочлена.
- •Локальная формула Тейлора (формула Тейлора с остаточным членом в форме Пеано).
- •Формула Тейлора с остаточным членом в форме Лагранжа и в форме Коши.
- •Разложение элементарных функций по формуле Тейлора.
- •Правило Лопиталя.
- •Условия монотонности функции.
- •Условия экстремума функции.
- •Условия выпуклости функции.
- •Д о к а з а т е л ь с т в о. Необходимость. Пусть функция является выпуклой. Выберем произвольно , , и покажем, что (9)
- •Точки перегиба графика функции.
- •Множество вещественных чисел (натуральные, целые, рациональные и иррациональные числа, модуль (абсолютная величина вещественного числа) и его свойства.
- •Комплексные числа.
Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
Теорема
1 (теорема Ролля). Пусть
функция
непрерывна на отрезке
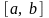 ,
дифференцируема
на интервале
,
дифференцируема
на интервале
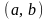 и на концах отрезка
принимает равные значения :
и на концах отрезка
принимает равные значения :
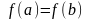 (1). Тогда существует такая точка
(1). Тогда существует такая точка
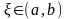 ,
что
,
что
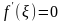 .
(2)
.
(2)
Замечание
1. Из
геометрических соображений теорема
Ролля очевидна: если выполнены условия
теоремы , то найдется такая точка
, что в точке
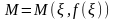 графика функции
касательная к графику параллельна оси
абсцисс и, следовательно тангенс угла
наклона касательно в этой точке равен
нулю , что равносильно (2).
графика функции
касательная к графику параллельна оси
абсцисс и, следовательно тангенс угла
наклона касательно в этой точке равен
нулю , что равносильно (2).
Д
о к а з а т е л ь с т в о. По первой теореме
Вейерштрасса (о непрерывной на отрезке
функции) функция
ограничена на отрезке
.
Следовательно числа
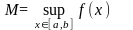 и
и
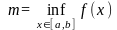 конечны.
конечны.
Если
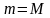 ,
то очевидно функция
является постоянной на отрезке
.
Тогда в качестве точки
,
для которой имеет место (2), можно взять
любую точку интервала
,
то очевидно функция
является постоянной на отрезке
.
Тогда в качестве точки
,
для которой имеет место (2), можно взять
любую точку интервала
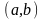 .
.
Пусть
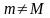 .
Тогда выполнено по крайней мере одно
из неравенств
.
Тогда выполнено по крайней мере одно
из неравенств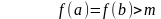 (3) и
(3) и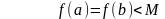 (4)
(4)
Пусть,
например, имеет место (4). По второй
теореме Вейерштрасса о непрерывной на
отрезке функции
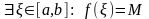 ,
при этом в силу (4)
,
при этом в силу (4)
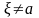 и
и
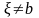 ,
т.е.
.
По определению числа
точка
является точкой глобального максимума
функции
.
Поэтому по теореме Ферма в этой точке
имеет место равенство (2) □
,
т.е.
.
По определению числа
точка
является точкой глобального максимума
функции
.
Поэтому по теореме Ферма в этой точке
имеет место равенство (2) □
Теорема
2 (Лагранжа).
Пусть функция
непрерывна на отрезке
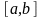 и дифференцируема на интервале
и дифференцируема на интервале
 .Тогда
найдется такая точка
,
что
.Тогда
найдется такая точка
,
что
 (5)
(5)
Замечание
2. Терема 2
также имеет простой геометрический
смысл. При выполнении ее условий на
графике функции
найдется такая точка
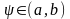 ,
что в точке
,
что в точке
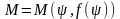 ,
касательная в которой к графику
параллельна хорде, стягивающей точки
,
касательная в которой к графику
параллельна хорде, стягивающей точки
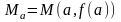 и
и
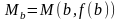 .
.
Д
о к а з а т е л ь с т в о. Рассмотрим функцию

Она
очевидно непрерывна на отрезке
,
дифференцируема на интервале
и на концах
отрезка
принимает
равные значения:
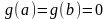 .Тогда
по теореме Ролля
.Тогда
по теореме Ролля
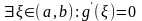 ,
т.е.
,
т.е.
 ,
а это равносильно равенству (5)□
,
а это равносильно равенству (5)□
Замечание
3. Формулу
(5) называют формулой конечных приращений
Лагранжа. Очевидно, она может быть
записана в виде
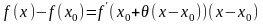
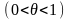
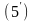
Для
этого достаточно положить в (5)
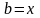 ,
,
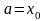 , a
, a
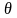 выбрать из условия
выбрать из условия
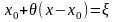 ,
т.е. положить
,
т.е. положить
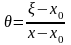 .
Нетрудно видеть, что формула
верна как при
.
Нетрудно видеть, что формула
верна как при
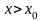 ,
так и при
,
так и при
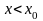 .
.
Теорема
3 (Коши). Пусть
функции
и
непрерывны на отрезке
и дифференцируемы на интервале
.
Тогда
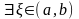 :
:
 (6)
(6)
Д
о к а з а т е л ь с т в о.
Рассмотрим
функцию
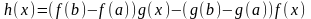 .
.
Она,
очевидно, удовлетворяет
условию
теоремы Ролля, согласно которой
 ,
т.е.
,
т.е.
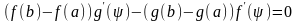 ,
что равносильно равенству (6)□
,
что равносильно равенству (6)□
Производные и дифференциалы высших порядков.
Понятие
производной порядка
.
Пусть функция
определена в некоторой окрестности
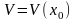 точки
и дифференцируема в этой окрестности,
т.е. дифференцируема в каждой точке
точки
и дифференцируема в этой окрестности,
т.е. дифференцируема в каждой точке
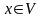 .
Тогда в окрестности
определена новая функция
.
Тогда в окрестности
определена новая функция
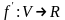 ,
которая, называется производной функции
на множестве
.
Если функция
,
которая, называется производной функции
на множестве
.
Если функция
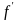 имеет в точке
производную, то ее называют второй
производной
или производной
второго порядка
функции
в этой точке и обозначают одним из
символов
имеет в точке
производную, то ее называют второй
производной
или производной
второго порядка
функции
в этой точке и обозначают одним из
символов
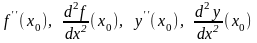 при этом часто аргумент – точку, в
которой вычисляется эта производная,
опускают. Таким образом
при этом часто аргумент – точку, в
которой вычисляется эта производная,
опускают. Таким образом
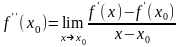 ,
при этом, если функция
дифференцируема в точке
,
т.е. имеет в ней конечную производную,
то говорят, что функция
дважды дифференцируема в этой точке.
,
при этом, если функция
дифференцируема в точке
,
т.е. имеет в ней конечную производную,
то говорят, что функция
дважды дифференцируема в этой точке.
Аналогично
понятию второй производной функции
в точке
вводится понятие третьей производной
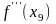 (ее обозначают также
(ее обозначают также
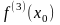 или
или
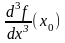 )
и, вообще производной любого порядка
.
)
и, вообще производной любого порядка
.
Точнее,
общее определение производной порядка
вводится индуктивно. А именно, если
функция
имеет в каждой точке
конечную производную
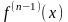 ,
то производная функции
,
то производная функции
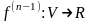 в точке
называется производной
-го
порядка функции
в точке
и обозначается одним из символов
в точке
называется производной
-го
порядка функции
в точке
и обозначается одним из символов
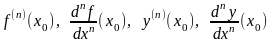 .
.
Таким
образом,
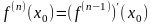
Наконец,
мы будем говорить, что функция
раз дифференцируема в точке
,
если в некоторой окрестности этой точки
она имеет конечную производную
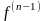 порядка
порядка
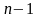 (а стало быть имеет и все производные
,
(а стало быть имеет и все производные
,
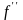 ,…,
)
и функция
дифференцируема в точке
.
,…,
)
и функция
дифференцируема в точке
.
В
соответствии с данным выше определением
производную функции
в точке
называют также первой производной
функции
в этой точке или, также, производной
первого порядка этой функции в точке
.
В дальнейшем условимся считать, что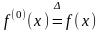 .
.
Непосредственно
из определения производной
-го
порядка вытекают следующие ее свойства: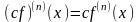 (
),
(
),
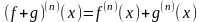 ,
где
и
–
раз дифференцируемые в точке
функции.
,
где
и
–
раз дифференцируемые в точке
функции.
Механический
смысл второй производной.
Если
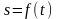 кинематический закон движения материальной
точки вдоль некоторой кривой, т.е. если
кинематический закон движения материальной
точки вдоль некоторой кривой, т.е. если
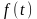 – путь, пройденный ей вдоль этой кривой
к моменту времени
– путь, пройденный ей вдоль этой кривой
к моменту времени
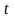 из некоторой начальной точки, то, как
известно, первая производная
из некоторой начальной точки, то, как
известно, первая производная
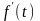 ,
если она существует, представляет собой
мгновенную скорость точки в момент
времени
.
,
если она существует, представляет собой
мгновенную скорость точки в момент
времени
.
Вместе
с тем отношение
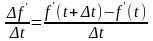 называют средним ускорением точки за
отрезок времени
называют средним ускорением точки за
отрезок времени
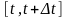 ,
а предел (если он существует)
,
а предел (если он существует)
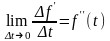 называют
ускорением точки в момент времени
.
называют
ускорением точки в момент времени
.
Таким
образом вторая производная
 – ускорение точки в момент времени
.
– ускорение точки в момент времени
.
Понятие
дифференциала порядка
.
Пусть функция
раз дифференцируема в точке
(в соответствии с данным выше определением
это означает, напомним, что в некоторой
окрестности этой точки она имеет конечные
производные до порядка
включительно, а в самой точке
имеет и конечную производную порядка
).
Тогда степенная функция
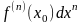 переменной
называется дифференциалом функции
в точке
порядка
и обозначается
переменной
называется дифференциалом функции
в точке
порядка
и обозначается
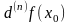 или
или
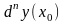 (короче также пишут
(короче также пишут
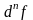 или
или
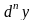 ).
).
Таким
образом, для дифференциала порядка
функции
в точке
имеем формулу
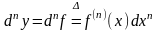 при этом понятия дифференциала и первого
дифференциала (дифференциала порядка
1) совпадают друг с другом.
при этом понятия дифференциала и первого
дифференциала (дифференциала порядка
1) совпадают друг с другом.
