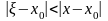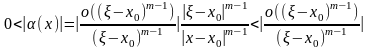- •Множества и действия над ними.
- •Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
- •Сюрьективные, инъективные и биективные отображения. Обратное отображение.
- •Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
- •Предел числовой последовательности. Сходящиеся и расходящиеся последовательности.
- •Арифметические свойства сходящихся последовательностей.
- •Предельный переход в неравенствах (для последовательностей).
- •Монотонные последовательности. Теорема о пределе монотонной последовательности.
- •Применение теоремы о пределе монотонной последовательности к вычислению пределов.
- •Число e.
- •Бесконечно малые и бесконечно большие последовательности.
- •Лемма о вложенных отрезках.
- •Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
- •Частичные пределы. Верхний и нижний пределы.
- •Фундаментальные последовательности. Критерий Коши сходимости числовой последовательности.
- •Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности.
- •Критерий Коши существования предела функции.
- •Локальные свойства функций имеющих предел.
- •Теорема о пределе суперпозиции.
- •Односторонние пределы.
- •Бесконечные пределы и пределы в бесконечности.
- •Бесконечно малые и бесконечно большие функции.
- •Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
- •Замечательные пределы
- •Асимптоты графика функции
- •Понятие непрерывной функции. Простейшие свойства непрерывных функций, в том числе, вытекающие из свойств предела.
- •Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры
- •Равномерно непрерывные функции. Теорема Кантора.
- •Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.
- •Теоремы Вейерштрасса о непрерывных на отрезке функциях.
- •Критерий непрерывности монотонной функции. Теорема об обратной функции к непрерывной и строго монотонной функции.
- •Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции в данной точке.
- •Дифференцируемые функции. Понятие дифференциала.
- •Арифметические операции с дифференцируемыми функциями.
- •Дифференцирование сложной функции.
- •Дифференцирование обратной функции.
- •Дифференцирование элементарных функций. Таблица производных.
- •Локальный экстремум функции. Теорема Ферма.
- •Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
- •Производные и дифференциалы высших порядков.
- •Формула Тейлора для многочлена.
- •Локальная формула Тейлора (формула Тейлора с остаточным членом в форме Пеано).
- •Формула Тейлора с остаточным членом в форме Лагранжа и в форме Коши.
- •Разложение элементарных функций по формуле Тейлора.
- •Правило Лопиталя.
- •Условия монотонности функции.
- •Условия экстремума функции.
- •Условия выпуклости функции.
- •Д о к а з а т е л ь с т в о. Необходимость. Пусть функция является выпуклой. Выберем произвольно , , и покажем, что (9)
- •Точки перегиба графика функции.
- •Множество вещественных чисел (натуральные, целые, рациональные и иррациональные числа, модуль (абсолютная величина вещественного числа) и его свойства.
- •Комплексные числа.
Формула Тейлора для многочлена.
Рассмотрим
некоторый многочлен степени
с вещественными коэффициентами:

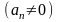 (1). Зададим
произвольное вещественное число
и в правой части равенства (1) представим
в виде
(1). Зададим
произвольное вещественное число
и в правой части равенства (1) представим
в виде
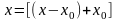 :
:
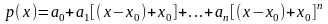 .
Раскрыв здесь квадратные скобки и
приведя подобные члены при одинаковых
степенях
.
Раскрыв здесь квадратные скобки и
приведя подобные члены при одинаковых
степенях
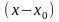 ,
в результате получим разложение
многочлена (1) по степеням
:
,
в результате получим разложение
многочлена (1) по степеням
:
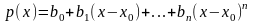 ,
(2), где
,
(2), где

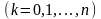 - постоянные, зависящие от исходных
коэффициентов и от числа
.
- постоянные, зависящие от исходных
коэффициентов и от числа
.
При
больших
,
на практике, указанный выше способ
разложения многочлена по степеням
весьма трудоемок. Оказывается, имеется
простой способ отыскания коэффициентов
разложения многочлена по степеням
.
Будем последовательно дифференцировать
равенство (2):

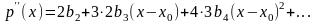
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
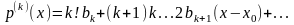
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
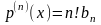 .
.
Полагая
в каждом из этих равенств
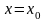 получим
получим
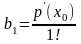
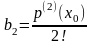
. . . . . . . . .
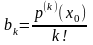
. . . . . . . . .
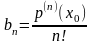
Если
кроме того положить
в (2), то считая, как обычно,
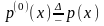 и
и
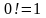 будем также иметь
будем также иметь
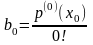 .
Таким образом, для коэффициентов
разложения (2) многочлена по степеням
имеем следующие формулы
,
.
Таким образом, для коэффициентов
разложения (2) многочлена по степеням
имеем следующие формулы
,
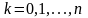 (3).
(3).
В
итоге заключаем, что разложение (2) можно
записать в виде:
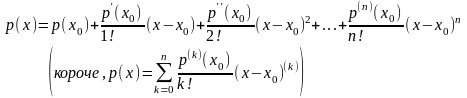 (4)
(4)
Формула
(4) называется формулой Тейлора в точке
для многочлена
 степени
.
Из вывода этой формулы следует, что
разложение многочлена по степеням
является единственным, так как коэффициенты
любого такого разложения однозначно
определяются по формулам (3).
степени
.
Из вывода этой формулы следует, что
разложение многочлена по степеням
является единственным, так как коэффициенты
любого такого разложения однозначно
определяются по формулам (3).
Формулу
Тейлора для многочлена
в
точке
 ,
то есть формулу
,
то есть формулу
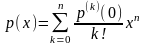 называют также формулой Маклорена.
называют также формулой Маклорена.
Локальная формула Тейлора (формула Тейлора с остаточным членом в форме Пеано).
Пусть
функция
раз дифференцируема в точке
.
Напомним, это означает, что существует
такая окрестность
точки
,
в которой определена сама функция
и существуют конечные производные
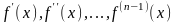 ,
,
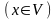 при этом в точке
существует также конечная производная
при этом в точке
существует также конечная производная
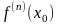 .
Поэтому, в частности, определен многочлен
.
Поэтому, в частности, определен многочлен
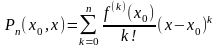 ,
который называется (
-ым)
многочленом Тейлора функции
в точке
.
Положим
,
который называется (
-ым)
многочленом Тейлора функции
в точке
.
Положим
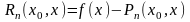 .
Тогда
.
Тогда
 Эта формула или, в более явном виде,
формула
Эта формула или, в более явном виде,
формула
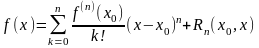 (1) называется
формулой
Тейлора
функции в точке
,
а функция
(1) называется
формулой
Тейлора
функции в точке
,
а функция
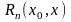 - остаточным
членом формулы Тейлора.
- остаточным
членом формулы Тейлора.
Ниже
будет доказано, что остаточный член
формулы Тейлора может быть записан в
виде
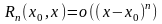 (при
)
(2).
(при
)
(2).
Остаточный
член в такой форме обычно называют
остаточным
членом в форме Пеано,
а формулу Тейлора с остаточным членом
в такой форме, т. е. формулу
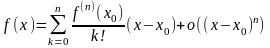 (3)
называют, соответственно, формулой
Тейлора с остаточным членом в форме
Пеано или,
также, локальной
формулой Тейлора.
(3)
называют, соответственно, формулой
Тейлора с остаточным членом в форме
Пеано или,
также, локальной
формулой Тейлора.
Лемма
1. Пусть
функция
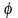 раз дифференцируема в точке
и
раз дифференцируема в точке
и
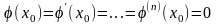 (4),
тогда
(4),
тогда
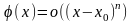 (5)
(5)
Д
о к а з а т е л ь с т в о (по индукции).
При
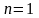 в силу дифференцируемости функции
в точке
имеем
в силу дифференцируемости функции
в точке
имеем
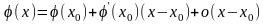 .
А так как по
условию (4)
.
А так как по
условию (4)
 ,
то это
означает, что
,
то это
означает, что
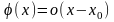 ,
таким образом,
при
утверждение леммы справедливо.
,
таким образом,
при
утверждение леммы справедливо.
Предположим,
что оно справедливо при
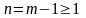 ,
и покажем, что тогда оно справедливо и
при
,
и покажем, что тогда оно справедливо и
при
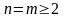 .
.
Действительно,
поскольку при
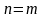 по условию (4), в частности,
по условию (4), в частности,
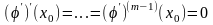 ,
то по индукционному предположению для
функции
,
то по индукционному предположению для
функции
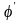 справедливо
справедливо
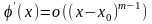 (6)
(6)
Далее,
так как функция
раз дифференцируема в точке
и
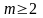 ,
то для любой точки
из некоторой окрестности
,
то для любой точки
из некоторой окрестности
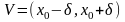 имеет
место формула конечных приращений
Лагранжа
имеет
место формула конечных приращений
Лагранжа
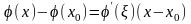 ,
(7) где
точка
,
(7) где
точка
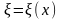 лежит между точками
и
.
Но так как
лежит между точками
и
.
Но так как
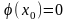 ,
то из формул (6) и (7) следует, что
,
то из формул (6) и (7) следует, что
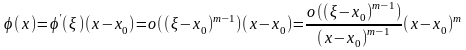 .
.
Полагая
здесь
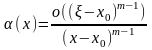 будем иметь
будем иметь
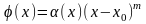 .
Поэтому равенство (5) при
будет
доказано, если будет показано, что
.
Поэтому равенство (5) при
будет
доказано, если будет показано, что
 (8)
(8)
Действительно, так как точка лежит между точками и , то
|
(9) |
и, следовательно,
|
(10) |
Остаётся
заметить, что в силу (9)
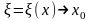 при
и, значит,
при
и, значит,
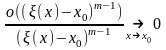
Тогда по принципу двух милиционеров из (10) следует (8)
Теорема 1. Если функция раз дифференцируема в точке , то для нее имеет место формула Тейлора с остаточным членом в форме Пеано (3).
Д о к а з а т е л ь с т в о. Достаточно заметить, что при выполнении условий теоремы функция
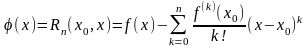
Удовлетворяет условиям леммы 1
Замечание 1. Вот другая, равносильная формулировка теоремы 1: Если функция имеет в точке конечные производные до порядка включительно, то для нее имеет место локальная формула Тейлора (3).