
- •Множества и действия над ними.
- •Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
- •Сюрьективные, инъективные и биективные отображения. Обратное отображение.
- •Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
- •Предел числовой последовательности. Сходящиеся и расходящиеся последовательности.
- •Арифметические свойства сходящихся последовательностей.
- •Предельный переход в неравенствах (для последовательностей).
- •Монотонные последовательности. Теорема о пределе монотонной последовательности.
- •Применение теоремы о пределе монотонной последовательности к вычислению пределов.
- •Число e.
- •Бесконечно малые и бесконечно большие последовательности.
- •Лемма о вложенных отрезках.
- •Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
- •Частичные пределы. Верхний и нижний пределы.
- •Фундаментальные последовательности. Критерий Коши сходимости числовой последовательности.
- •Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности.
- •Критерий Коши существования предела функции.
- •Локальные свойства функций имеющих предел.
- •Теорема о пределе суперпозиции.
- •Односторонние пределы.
- •Бесконечные пределы и пределы в бесконечности.
- •Бесконечно малые и бесконечно большие функции.
- •Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
- •Замечательные пределы
- •Асимптоты графика функции
- •Понятие непрерывной функции. Простейшие свойства непрерывных функций, в том числе, вытекающие из свойств предела.
- •Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры
- •Равномерно непрерывные функции. Теорема Кантора.
- •Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.
- •Теоремы Вейерштрасса о непрерывных на отрезке функциях.
- •Критерий непрерывности монотонной функции. Теорема об обратной функции к непрерывной и строго монотонной функции.
- •Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции в данной точке.
- •Дифференцируемые функции. Понятие дифференциала.
- •Арифметические операции с дифференцируемыми функциями.
- •Дифференцирование сложной функции.
- •Дифференцирование обратной функции.
- •Дифференцирование элементарных функций. Таблица производных.
- •Локальный экстремум функции. Теорема Ферма.
- •Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
- •Производные и дифференциалы высших порядков.
- •Формула Тейлора для многочлена.
- •Локальная формула Тейлора (формула Тейлора с остаточным членом в форме Пеано).
- •Формула Тейлора с остаточным членом в форме Лагранжа и в форме Коши.
- •Разложение элементарных функций по формуле Тейлора.
- •Правило Лопиталя.
- •Условия монотонности функции.
- •Условия экстремума функции.
- •Условия выпуклости функции.
- •Д о к а з а т е л ь с т в о. Необходимость. Пусть функция является выпуклой. Выберем произвольно , , и покажем, что (9)
- •Точки перегиба графика функции.
- •Множество вещественных чисел (натуральные, целые, рациональные и иррациональные числа, модуль (абсолютная величина вещественного числа) и его свойства.
- •Комплексные числа.
Предельный переход в неравенствах (для последовательностей).
Лемма
1. Если
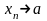 ,
,
 и
и
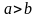 ,
то существует такой номер
,
то существует такой номер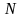 ,
что
,
что
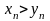
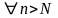 .
.
Д о к а з а т е л ь с т в о разбирается на лекции.
Теорема
2 (о предельном
переходе в неравенстве). Если
каждая из последовательностей
и
сходится и
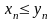 ,
то
,
то
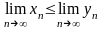 .
.
В
самом деле, элементы последовательности
{yn - xn}
неотрицательны, а поэтому неотрицателен
и ее предел 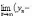
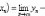
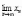 .
Отсюда следует, что
.
Отсюда следует, что
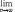

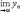
Замечание.
Из того,
что
,
и
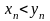 ,
в общем случае, следует только, что
,
а не то, что
,
в общем случае, следует только, что
,
а не то, что
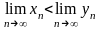 .
Для этого достаточно рассмотреть,
например, следующие последовательности
и
:
.
Для этого достаточно рассмотреть,
например, следующие последовательности
и
:
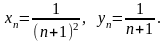
Теорема
3 (принцип
двух милиционеров).
Если
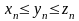
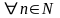 ,
а последовательности
и
,
а последовательности
и
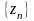 сходятся и
имеют один и тот же предел, то сходится
и последовательность
,при
этом
сходятся и
имеют один и тот же предел, то сходится
и последовательность
,при
этом
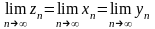 .
.
Д
о к а з а т е л ь с т в о
Пусть
и
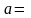
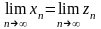 .
(8)
Требуется доказать, что
.
(8)
Требуется доказать, что
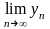 (9).
Для этого выберем произвольное
и покажем, что
такое,
что
(9).
Для этого выберем произвольное
и покажем, что
такое,
что
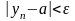 (10)
Поскольку имеют место равенства (8), то
найдется такой номер
,
что
и
(10)
Поскольку имеют место равенства (8), то
найдется такой номер
,
что
и
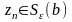 ,
а так как
,
то отсюда следует, что
,
а так как
,
то отсюда следует, что
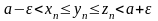 .
Следовательно
.
Следовательно
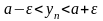 ,
что равносильно (10), а это в силу
произвольности
(9) □
,
что равносильно (10), а это в силу
произвольности
(9) □
Монотонные последовательности. Теорема о пределе монотонной последовательности.
Определение 1. Последовательность называется
а)
возрастающей,
если
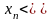
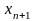 ;
;
б)
неубывающей,
если
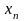
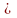 ;
;
в) убывающей, если ;
г)
невозрастающей,
если
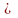 ;
;
д) монотонной, если она относится к одному из указанных выше типов а) – г);
е) строго монотонной, если она является либо возрастающей, либо убывающей.
Теорема 1. Всякая ограниченная монотонная последовательность сходится.
Поскольку
всякая сходящаяся, и даже необязательно
монотонная, последовательность
ограничена, то из этой теоремы вытекает
такое Следствие.
Для того,
чтобы монотонная последовательность
была сходящейся, необходимо и достаточно,
чтобы она была ограниченной.
Всякая неубывающая последовательность
,
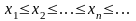 ограничена снизу (числом
ограничена снизу (числом
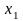 ).
Следовательно, для ее ограниченности
достаточно, чтобы она была ограниченной
сверху. Поэтому справедливы следующие
уточнения теорема и ее следствия.
).
Следовательно, для ее ограниченности
достаточно, чтобы она была ограниченной
сверху. Поэтому справедливы следующие
уточнения теорема и ее следствия.
Теорема
2. Всякая
неубывающая,
ограниченная сверху числовая
последовательность
сходится, при этом
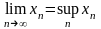
Следствие. Для того, чтобы неубывающая числовая последовательность была сходящейся необходимо и достаточно, чтобы она была ограничена сверху.Аналогично, для невозрастающих последовательностей справедливы следующие утверждения:
Теорема
3. Всякая
невозрастающая,
ограниченная снизу числовая
последовательность
сходится, при этом
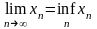
Следствие. Для того, чтобы невозрастающая числовая последовательность была сходящейся необходимо и достаточно, чтобы она была ограничена снизу.
Применение теоремы о пределе монотонной последовательности к вычислению пределов.
П
р и м е р 1.
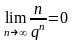 ,
если q
> 1. Действительно, здесь
=
,
если q
> 1. Действительно, здесь
=
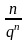 ,
.
Поэтому
=
,
.
Поэтому
=
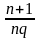 ,
(1) а
так как
,
(1) а
так как
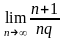 =
=
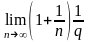 =
=
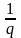
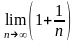 =
< 1, то найдется номер N,
такой, что при
> N
будем иметь
=
< 1, то найдется номер N,
такой, что при
> N
будем иметь
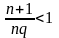 и следовательно, при тех же
<
.
Следовательно, если отбросить первые
N
членов рассматриваемой последовательности,
то оставшиеся ее члены будут составлять
монотонно убывающую последовательность,
которая к тому же ограничена снизу (все
ее члены положительные) и в силу этого
сходится (теорема 3). Поскольку отбрасывание
конечного числа членов последовательности
не влияет на ее сходимость, то это
означает, что сходится и исходная
последовательность.
и следовательно, при тех же
<
.
Следовательно, если отбросить первые
N
членов рассматриваемой последовательности,
то оставшиеся ее члены будут составлять
монотонно убывающую последовательность,
которая к тому же ограничена снизу (все
ее члены положительные) и в силу этого
сходится (теорема 3). Поскольку отбрасывание
конечного числа членов последовательности
не влияет на ее сходимость, то это
означает, что сходится и исходная
последовательность.
Найдем
теперь ее предел. Пусть
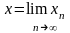 .
Тогда с учетом равенства (1) будем иметь
.
Тогда с учетом равенства (1) будем иметь
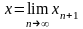 =
=
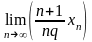 =
∙
=
∙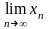 =
=
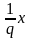 .
Поэтому
.
Поэтому
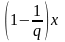 = 0 и, следовательно,
= 0 □
= 0 и, следовательно,
= 0 □
С
л е д с т в и е 1.
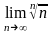 = 1. Д
о к а з а т е л ь с т в о. При фиксированном
по доказанному в 1-м примере
= 1. Д
о к а з а т е л ь с т в о. При фиксированном
по доказанному в 1-м примере
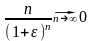 (здесь
(здесь
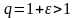 ).
Поэтому найдется
).
Поэтому найдется
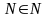 такое, что
при
будем иметь
такое, что
при
будем иметь
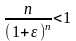 и, следовательно,
и, следовательно,
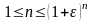 при
.
А тогда
при
.
А тогда
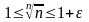 при
и тем более
при
и тем более
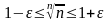 при
.
при
.
В силу произвольности это и означает, что = 1 □
С
л е д с т в и е 2.
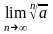 = 1
при любом а > 0.
= 1
при любом а > 0.
П
р и м е р 2.
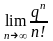 = 0 (здесь
= 0 (здесь
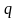 - любое действительное число,
- любое действительное число,
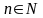 ,
,
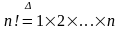 )
)
