
- •Множества и действия над ними.
- •Понятие отображения, образ и прообраз множества при отображении, суперпозиция отображений, сужение отображения, график отображения.
- •Сюрьективные, инъективные и биективные отображения. Обратное отображение.
- •Аксиома непрерывности множества вещественных чисел. Точные грани числовых множеств.
- •Предел числовой последовательности. Сходящиеся и расходящиеся последовательности.
- •Арифметические свойства сходящихся последовательностей.
- •Предельный переход в неравенствах (для последовательностей).
- •Монотонные последовательности. Теорема о пределе монотонной последовательности.
- •Применение теоремы о пределе монотонной последовательности к вычислению пределов.
- •Число e.
- •Бесконечно малые и бесконечно большие последовательности.
- •Лемма о вложенных отрезках.
- •Подпоследовательности. Теорема Больцано-Вейерштрасса об ограниченной последовательности.
- •Частичные пределы. Верхний и нижний пределы.
- •Фундаментальные последовательности. Критерий Коши сходимости числовой последовательности.
- •Предел функции: два определения и их эквивалентность. Теоремы о пределе функции, вытекающие из теорем о пределе числовой последовательности.
- •Критерий Коши существования предела функции.
- •Локальные свойства функций имеющих предел.
- •Теорема о пределе суперпозиции.
- •Односторонние пределы.
- •Бесконечные пределы и пределы в бесконечности.
- •Бесконечно малые и бесконечно большие функции.
- •Символы о-малое и о-большое, эквивалентные б.М. И б.Б.
- •Замечательные пределы
- •Асимптоты графика функции
- •Понятие непрерывной функции. Простейшие свойства непрерывных функций, в том числе, вытекающие из свойств предела.
- •Точки разрыва функции и их классификация. Примеры: функция Дирихле и другие примеры
- •Равномерно непрерывные функции. Теорема Кантора.
- •Теоремы Больцано-Коши о промежуточных значениях непрерывной функции.
- •Теоремы Вейерштрасса о непрерывных на отрезке функциях.
- •Критерий непрерывности монотонной функции. Теорема об обратной функции к непрерывной и строго монотонной функции.
- •Понятие производной, ее геометрический и механический смысл. Уравнение касательной к графику функции в данной точке.
- •Дифференцируемые функции. Понятие дифференциала.
- •Арифметические операции с дифференцируемыми функциями.
- •Дифференцирование сложной функции.
- •Дифференцирование обратной функции.
- •Дифференцирование элементарных функций. Таблица производных.
- •Локальный экстремум функции. Теорема Ферма.
- •Теоремы о среднем значении для дифференцируемых функций: теоремы Роля, Лагранжа и Коши.
- •Производные и дифференциалы высших порядков.
- •Формула Тейлора для многочлена.
- •Локальная формула Тейлора (формула Тейлора с остаточным членом в форме Пеано).
- •Формула Тейлора с остаточным членом в форме Лагранжа и в форме Коши.
- •Разложение элементарных функций по формуле Тейлора.
- •Правило Лопиталя.
- •Условия монотонности функции.
- •Условия экстремума функции.
- •Условия выпуклости функции.
- •Д о к а з а т е л ь с т в о. Необходимость. Пусть функция является выпуклой. Выберем произвольно , , и покажем, что (9)
- •Точки перегиба графика функции.
- •Множество вещественных чисел (натуральные, целые, рациональные и иррациональные числа, модуль (абсолютная величина вещественного числа) и его свойства.
- •Комплексные числа.
Дифференцирование элементарных функций. Таблица производных.
nо 1. Таблица производных
Элементарные
функции (за исключением функций
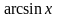 и
и
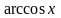 )
дифференцируемы в своих областях
определения, причем справедливы следующие
формулы (они обосновываются в следующих
пунктах):
)
дифференцируемы в своих областях
определения, причем справедливы следующие
формулы (они обосновываются в следующих
пунктах):
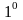 .
.

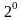 .
.

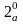 .
.

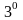 .
.
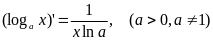
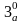 .
.
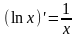
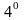 .
.
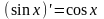
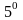 .
.

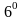 .
.

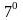 .
.
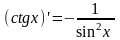
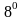 .
.
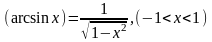
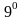 .
.
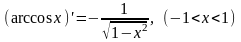
 .
.
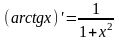
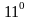 .
.
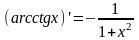
nо 2. Показательная и логарифмическая функции.
Здесь
будут установлены формулы
,
,
и
из предыдущего пункта. Прежде всего,
напомним, что
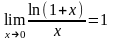 (1) и
(1) и
 (2)
(2)
Теперь
используя равенство (2) и то, что постоянную
можно выносить за знак предела получим:
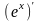 =
=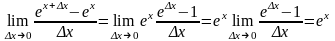 .
Таким образом установлена
формула
.
.
Таким образом установлена
формула
.
Далее,
так как функция
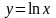 является обратной к функции
является обратной к функции
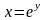 ,
по формуле для производной обратной
функции имеем:
,
по формуле для производной обратной
функции имеем:
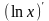 =
= .
Следовательно,
установлена и формула
.
.
Следовательно,
установлена и формула
.
Для
вывода формулы
установим формулу дифференцирования
показательно-степенной функции
 где
где
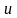 и
и
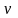 – дифференцируемые на некотором
промежутке
– дифференцируемые на некотором
промежутке
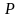 функции, причем
функции, причем
 на
.
на
.
Используя
формулу для производной сложной функции,
формулы
и
,
а также формулу для производной
произведения функций будем иметь
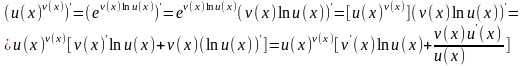
Таким
образом,
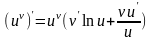 .
.
В
частности, если здесь
 ,
а
,
а
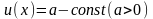 ,
то
,
то
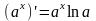 ,
т.е. установлена
и формула
.
,
т.е. установлена
и формула
.
Формула
вытекает из
формулы 20
в силу формулы дифференцирования
обратной функции:
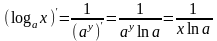 (здесь
(здесь
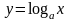 ,
,
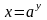 ).
).
nо 3. Производная степенной функции.
Предварительно
представив степенную функцию
 (
(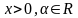 )
в виде
)
в виде
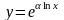 ее производную вычислим с помощью
формулы дифференцирования сложной
функции:
ее производную вычислим с помощью
формулы дифференцирования сложной
функции:
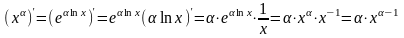 Формула
,
таким образом, также доказана.
Формула
,
таким образом, также доказана.
nо 4. Тригонометрические функции.
Используя
формулу
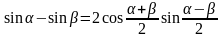 ,
а также
известный замечательный предел
,
а также
известный замечательный предел
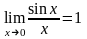 ,
по
определению производной с учетом
непрерывности функции
,
по
определению производной с учетом
непрерывности функции
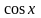 будем
иметь
будем
иметь
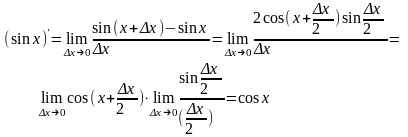
Далее,
по правилу дифференцирования сложной
функции получим

Производные
от функции
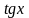 и
и
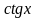 вычисляются с использованием установленных
выше формул
и
и формул дифференцирования частного.
Читателю предлагается сделать это
самостоятельно.
вычисляются с использованием установленных
выше формул
и
и формул дифференцирования частного.
Читателю предлагается сделать это
самостоятельно.
nо 5. Обратные тригонометрические функции.
Формулы
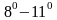 выводятся с помощью формулы для
производной обратной функции и одной
из соответствующих
выводятся с помощью формулы для
производной обратной функции и одной
из соответствующих
 .
.
Например,
функция
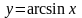
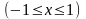 является
обратной к функции
является
обратной к функции
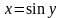 ,
(
,
(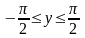 ).
Поэтому
).
Поэтому
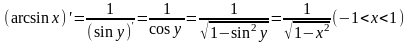 .(Перед
радикалом здесь берется знак «+»,
поскольку
.(Перед
радикалом здесь берется знак «+»,
поскольку
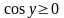 при
).
Аналогично вычисляется производная
от функции
при
).
Аналогично вычисляется производная
от функции
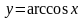 .
.
Далее,
функция
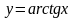
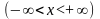 является обратной к функции
является обратной к функции
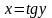
 .
Поэтому
.
Поэтому
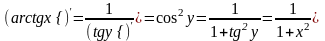 .
Аналогично вычисляется производная от
функции
.
Аналогично вычисляется производная от
функции
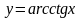 .
.
Локальный экстремум функции. Теорема Ферма.
Определение
1. Пусть
функция
определена
на множестве
и
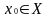 .
Говорят, что в точке
.
Говорят, что в точке
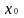 функция
имеет локальный минимум
(локальный
максимум)
,
если существует такая окрестность
этой точки,
что
функция
имеет локальный минимум
(локальный
максимум)
,
если существует такая окрестность
этой точки,
что
 (
( ),
(1) при
этом точку
называют точкой
локального
минимума
(локального
максимума)
функции.
),
(1) при
этом точку
называют точкой
локального
минимума
(локального
максимума)
функции.
Замечание
1. Если
внутренняя точка множества
,
т.е. если она принадлежит ему вместе с
некоторой своей окрестностью то в
условии (1) вместо «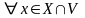 »
можно писать «
»
можно писать «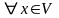 »,
считая без ущерба для общности, что
»,
считая без ущерба для общности, что
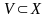 .
.
Замечание 2. Если в точке функция имеет или локальный минимум или локальный максимум, то говорят, что она имеет в этой точке локальный экстремум, при этом точку называют точкой локального экстремума.
Замечание
3. Всякая
точка максимума (минимума) фуркции
на множестве
, т.е. всякая
точка
,
для которой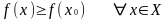 ;
(
;
( ),
иногда называется точкой
глобального минимума (глобального
максимума)
функции
на множестве
.
),
иногда называется точкой
глобального минимума (глобального
максимума)
функции
на множестве
.
Очевидно, что всякая точка глобального экстремума, т.е. глобального максимума или глобального минимума, является также и точкой локального экстремума.
Теорема
1(Ферма).
Пусть функция
определена на множестве
,
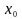 -
внутренняя точка множества
и функция
дифференцируема в этой точке .Тогда,
если
– точка локального экстремума этой
функции, то
-
внутренняя точка множества
и функция
дифференцируема в этой точке .Тогда,
если
– точка локального экстремума этой
функции, то
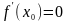 (2)
(2)
Д
о к а з а т е л ь с т в о. Для определенности
будем считать , что
─ точка
локального минимума . Тогда
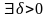 такое, что
такое, что
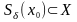 (
─
внутренняя
точка
)
и
(
─
внутренняя
точка
)
и
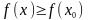
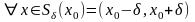 .
.
Поэтому

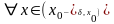 (3)
(3)
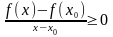
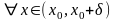 .
(4)
.
(4)
Из
неравенства (3) , в силу дифференцируемости
функции
в точке
и теоремы
о предельном переходе в неравенстве,
очевидно следует, что
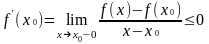 (5), а
из неравенства (4) , в силу того же, в
свою очередь, следует , что
(5), а
из неравенства (4) , в силу того же, в
свою очередь, следует , что
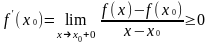 (6).
Из неравенств
(5) и (6) и вытекает равенство (2) □
(6).
Из неравенств
(5) и (6) и вытекает равенство (2) □
