Обработка результатов измерений

1. Вычислить среднее время падения маятника и занести его в табл. 7.1.

2. Вычислить погрешность измерения времени падения, занося все промежуточные значения в табл. 7.1.

3. Округлить полученный результат и записать его в окончательном виде с погрешностью.

4. Вычислить по формуле (7.1) момент инерции маятника Максвелла.

5. Вычислить абсолютную погрешность измерения момента инерции маятника, как косвенного измерения. При этом удобно вычислить сначала относительную погрешность

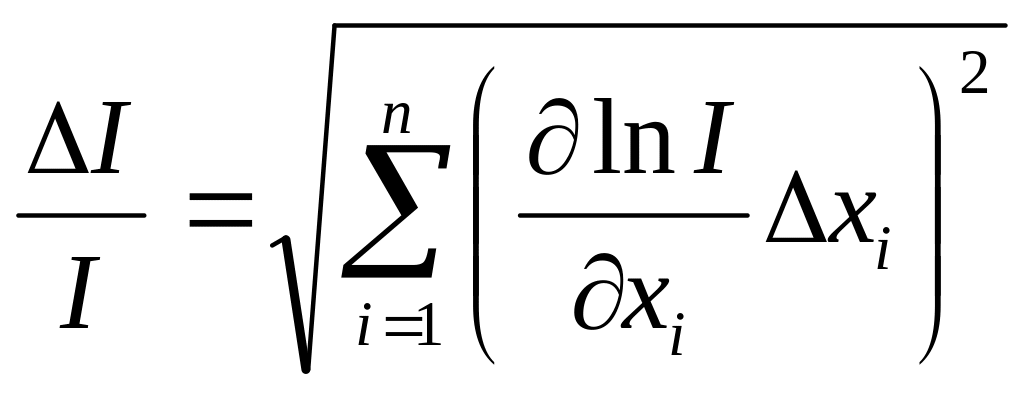
где x_i – независимые аргументы функции I, измеренные с погрешностью .

Таким образом, после несложных преобразований и с учетом   получаем

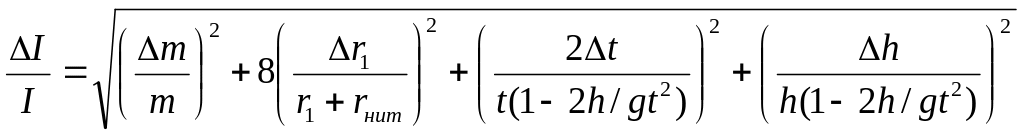
Такой способ вычислений удобен тем, что можно оценить по отдельности относительный вклад в суммарную погрешность погрешностей каждой из измеряемых величин и пренебречь теми слагаемыми, вклад которых невелик, т.е. величина которых на три-четыре и больше порядков меньше остальных.

Зная относительную погрешность измерения, легко найти и абсолютную погрешность.

6. Вычислить теоретическое значение момента инерции маятника по формуле (7.3).

7. Записать окончательный результат вычислений момента инерции с погрешностью и теоретическое значение этой величины. Сопоставить их.

8. Вычислить кинетическую энергию маятника Максвелла в момент прохождения им нижней точки по (7.2) и сравнить ее с потенциальной энергией mgh для проверки выполнения закона сохранения энергии.

Контрольные вопросы и задания

1. Что такое момент инерции твердого тела относительно заданной оси?

2. Сформулируйте основной закон динамики твердого тела.

3. Что такое момент силы и как определить его направление?

4. Как направлено угловое ускорение при вращательном движении твердого тела?

5. Провести аналогию между характеристиками вращательного и поступательного движения.

Литература: [1, § 28, 29, 32, 34]; [2, § 33-35, 36, 37, 79]; [4, § 4.1-4.3 ]; [5].

Лабораторная работа № 8

Определение момента инерции твердых тел с помощью крутильных колебаний

Цель работы – экспериментальное определение моментов инерции твёрдых тел относительно различных осей вращения.

Приборы и принадлежности: крутильный маятник FPM-05, твёрдые тела различной формы, блок миллисекундомера.

Краткие сведения из теории

П

Рис.15.1

ри описании вращательного движения твёрдого тела вводится понятие момента инерции – физической величины, характеризующей распределение масс в теле и являющейся, наряду с массой, мерой инертности тела при вращательном движении. Моментом инерции тела относительно некоторой оси называется величина, равная сумме произведений элементарных масс на квадраты их расстояний от данной оси:

.

Если вещество в теле распределено непрерывно, то вычисление его момента инерции сводится к вычислению интеграла

где dm – масса элемента объема тела, находящегося на расстоянии r от оси вращения.

Рассмотрим в качестве примера плоскую прямоугольную пластинку со сторонами a и b и массой m.

Рис. 8.1

Разобьем пластину на бесконечно узкие полоски шириной dx и массой каждая (рис. 8.1).

Момент инерции пластинки относительно оси z, лежащей в плоскости пластины и проходящей через ее центр масс равен

В ряде случаев нахождение момента инерции значительно упрощается, если воспользоваться теоремой Штейнера: момент инерции тела относительно произвольной оси z равен моменту инерции относительно оси z_C, параллельной данной и проходящей через центр масс тела, плюс произведение массы тела на квадрат расстояния a между осями:

Найдем теперь момент инерции однородного прямоугольного параллелепипеда относительно оси z, проходящей через центр масс параллелепипеда (рис. 8.2):

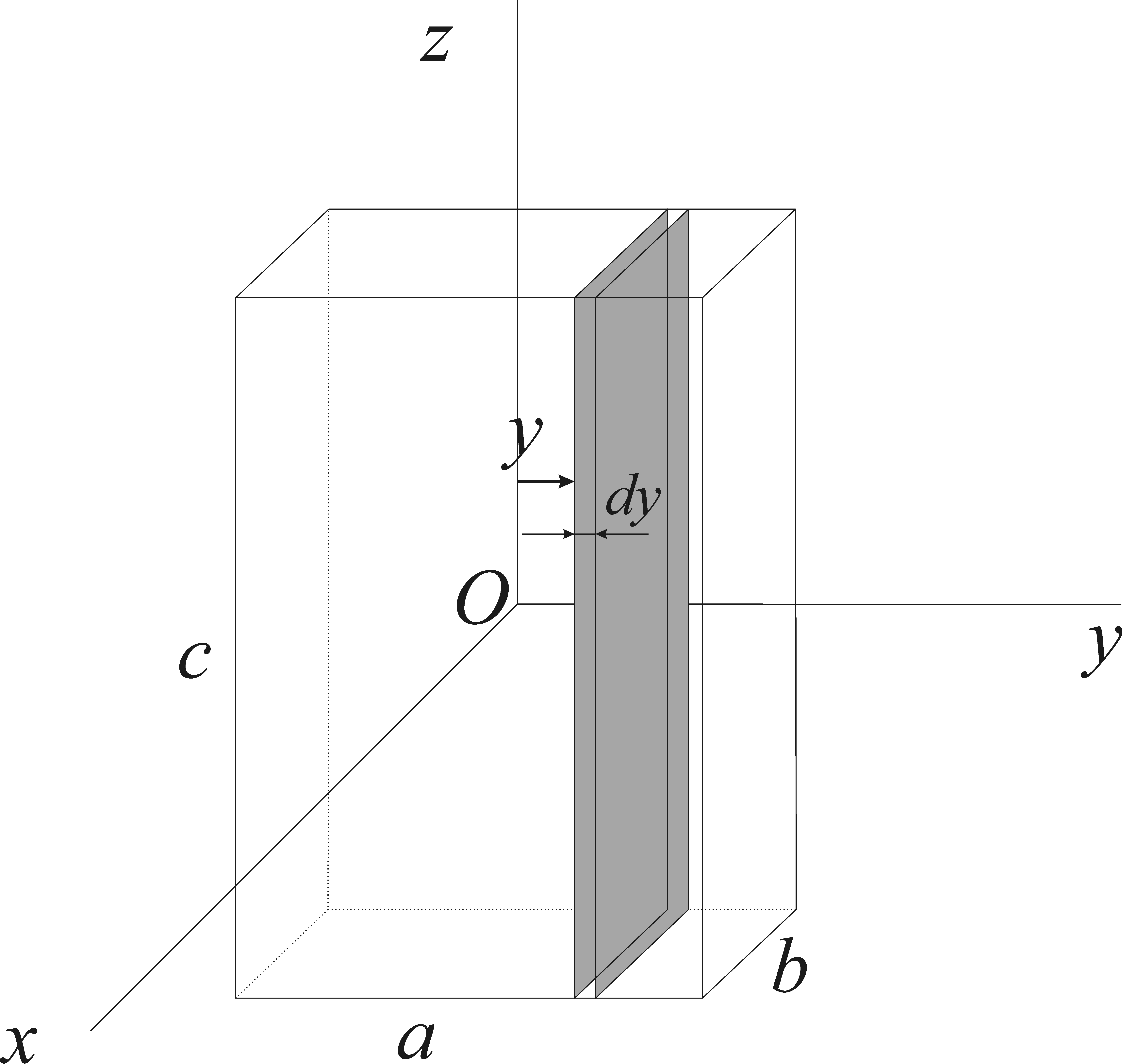
Рис. 8.2

Для этого разобьем параллелепипед на бесконечно тонкие пластинки, параллельные плоскости zx, толщиной dy и массой каждая. Согласно теореме Штейнера момент инерции такой пластинки относительно оси z равен

Для параллелепипеда, интегрируя, получаем

Таким образом,

Аналогично можно показать, что моменты инерции параллелепипеда относительно осей x и y равны

Момент инерции тела относительно произвольно ориентированной оси v, проходящей через центр масс тела, определяется соотношением где - направляющие косинусы.

Для момента инерции однородного прямоугольного параллелепипеда относительно оси АВ (диагональ параллелепипеда) получаем:

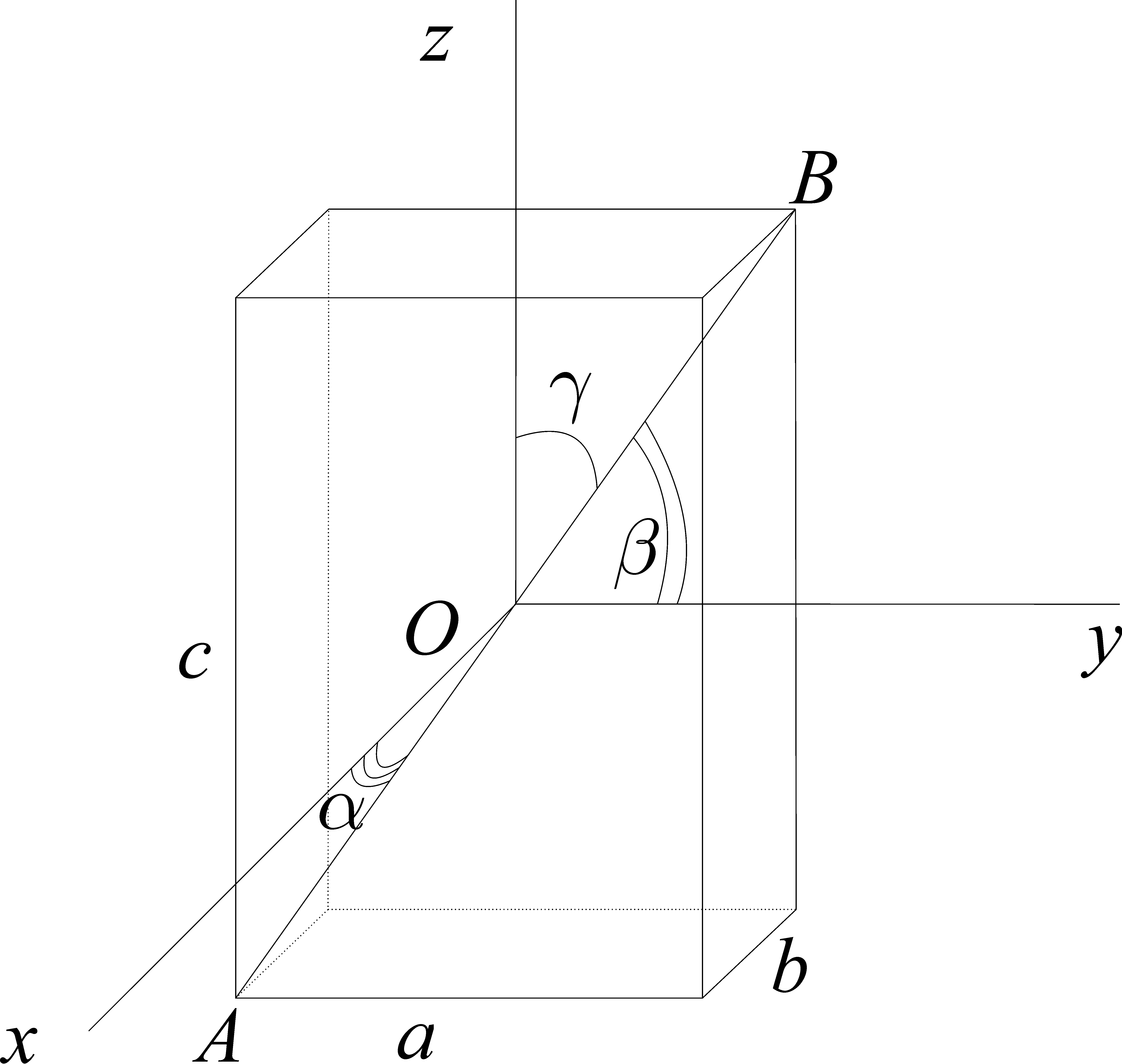
Рис. 8.3

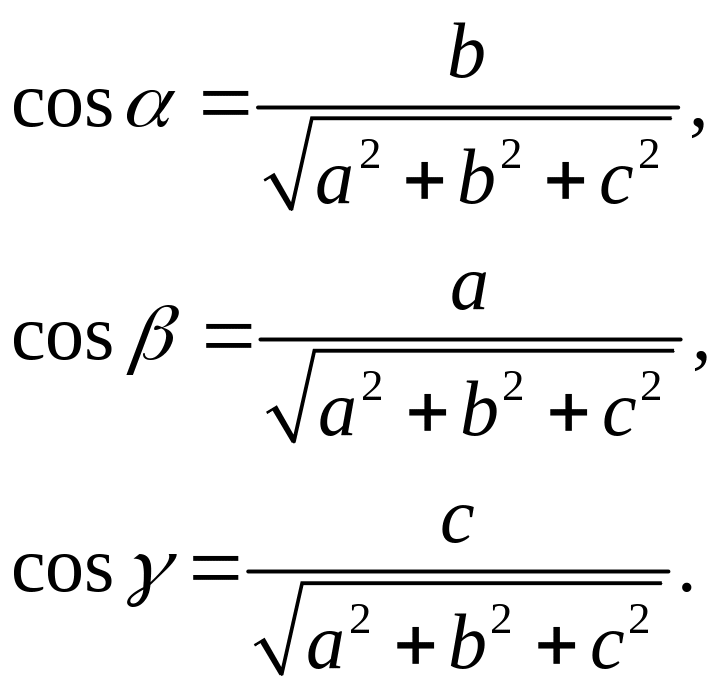
Тогда, подставляя (8.1 – 8.3), получаем