14 Электродинамика медленных процессов в плазме. Ионно – звуковые волны. Магнитная гидродинамика.

14.1 Ионно-звуковые волны малой амплитуды. Ионы очень слабо влияют на высокочастотные волновые процессы в плазме благодаря большому отличию масс электронов и ионов. Однако, влияние ионов чрезвычайно существенно для низкочастотных волн. Сейчас рассмотрим одну из таких ситуаций. Пусть имеется сильная неизотермичность изотропной плазмы. Равновесное максвелловское распределение устанавливается в газе в результате столкновений между частицами. В плазме с малой частотой столкновений время свободного пробега частиц очень велико и она может долго находиться в неравновесном состоянии. Особенно долго может сохраняться двухтемпературное состояние. Распределения электронов и ионов при этом максвелловские, но температура электронов не равна температуре ионов . В экспериментах очень часто выполняется неравенство >> , Это связано с тем, что при многих методах нагрева плазмы первоначально нагреваются электроны, а затем энергия постепенно передается от электронов к ионам. Законы сохранения энергии и импульса при упругих столкновениях показывают, что обмен энергиями между частицами одного сорта происходит в раз быстрее, чем обмен энергиями между электронами и ионами. Поэтому быстрее всего устанавливается максвелловское распределение в каждой из компонент (электронной и ионной) порознь. После этого происходит медленное выравнивание температур. Рассмотрим сейчас двухкомпонентную плазму, в которой выполнено условие >> и будем интересоваться медленным (низкочастотным) процессом, в котором упорядоченные скорости электронов и ионов одного порядка малости (в высокочастотных процессах упорядоченная скорость электронов гораздо больше, чем скорость ионов, допустимо использования приближения неподвижных ионов). Такие медленные волны впервые были исследованы Ленгмюром и Тонксом (1929 г.). Напишем линеаризованные уравнения движения горячих электронов и холодных ионов (будем интересоваться волнами малой амплитуды):

, . (14.1)

В уравнении движения ионной компоненты отсутствует учет члена , так как . Если просуммировать эти уравнения, то получим

.

Так как и скорости и одного порядка малости в низкочастотных процессах (доказательство этого будет сделано в конце раздела 14.1), то слагаемым можно пренебречь и написать

. (14.2)

Получился «гибрид»: в левой части уравнения (14.2) стоят величины, относящиеся к ионам, а в правой части стоят величины, относящиеся к электронам. Пренебрежение членом указывает на то, что это можно сделать и в уравнении движения электронов (пренебрежение инерцией электронов):

. (14.2.А)

Из этого уравнения следует, что электрическое поле потенциально

, , , (14.2.В)

Уравнение состояния для давления возьмем в виде

,

где величины, отмеченные индексом нуль характеризуют однородное стационарное невозмущенное состояние, . Из уравнения (14.2.В) следует .

Закон Кулона

позволяет найти связь . (14.3)

Уравнение движения (14.1) дает возможность получить взаимосвязь между и

. (14.4)

Из (14.3) и (14.4) получаются представления для фурье – образов

, . (14.5)

Подстановка этих представлений в уравнение неразрывности

после перехода к фурье – образам дает дисперсионное уравнение ,(14.6)

где 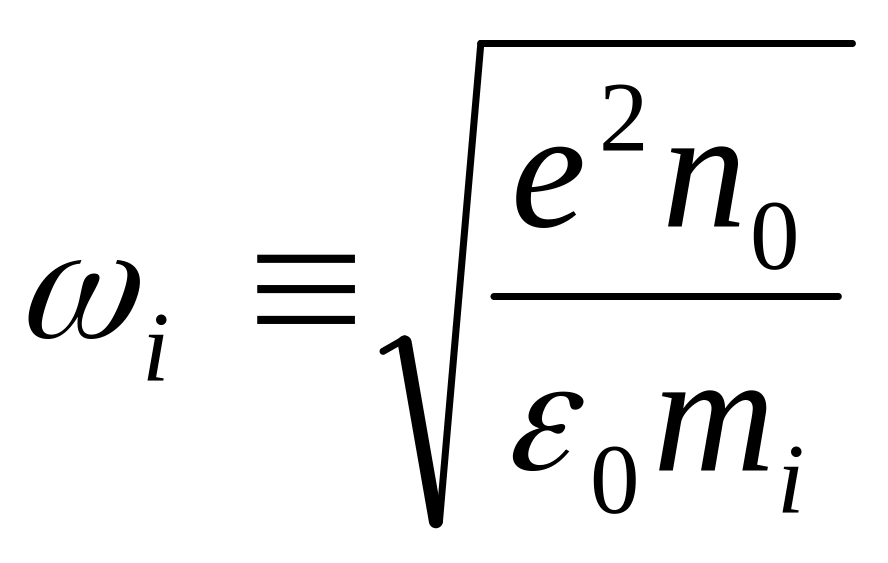- ионная плазменная частота. Решение уравнения (14.6) можно представить в виде , либо ,

где - скорость ионного звука, она определяется температурой электронов массой ионов. Отметим некоторые дисперсионные свойства:

1. При 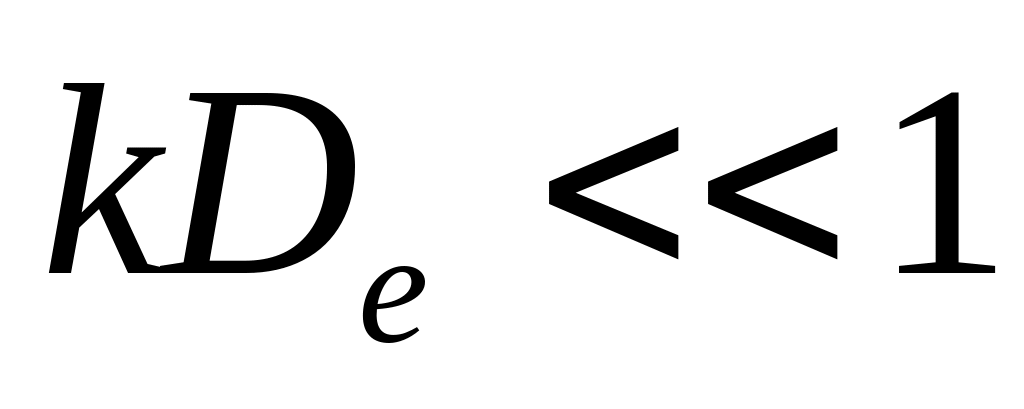(длинноволновое приближение или пренебрежение влиянием дисперсии в таком приближении электро - нейтральность нарушается слабо) 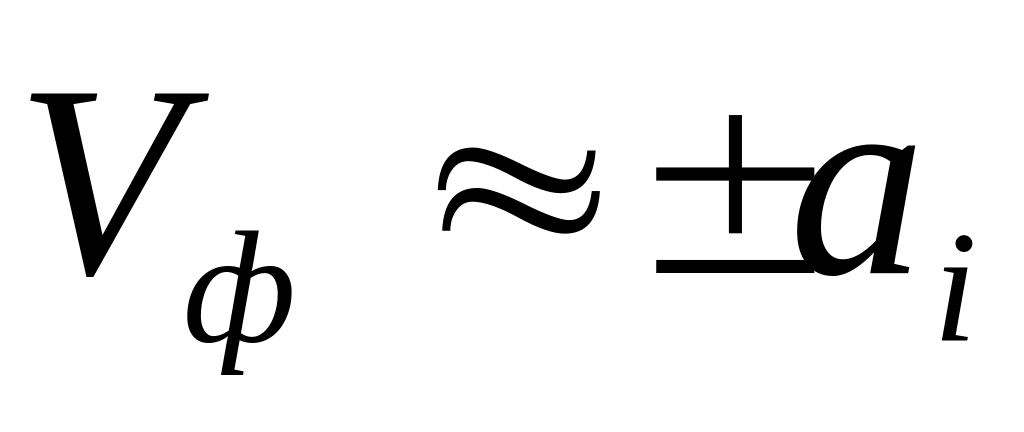- фазовая скорость близка к скорости ионного звука. Именно по этой причине волна называется ионно – звуковой.

2. При имеет место .

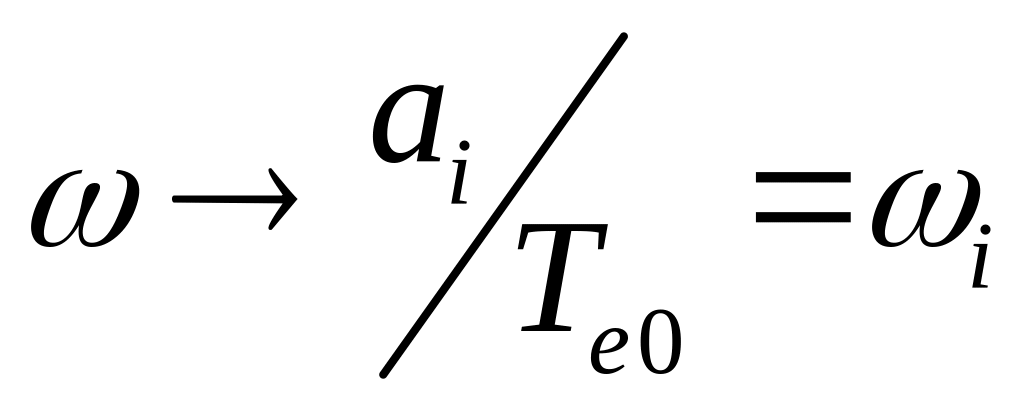3. В рассматриваемом описании процесса 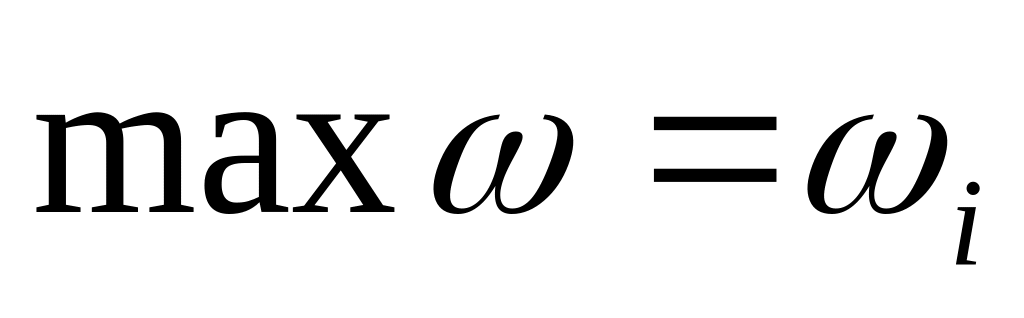, т.е. не возможен переход к бесконечно высоким частотам. Нет предельного перехода свойств среды в свойства вакуума. Такая ситуация типична для идеализированного описания медленных процессов (аналогичным примером может служить магнитная гидродинамика).

Обсудим теперь условия применимости ионно – звукового приближения.

• (приближение низких частот).

• (большая неизотермичность плазмы). Нарушение этого условия приводит к возникновению сильного затухания волны (в частности, существенна роль затухания Ландау).

• .

• .

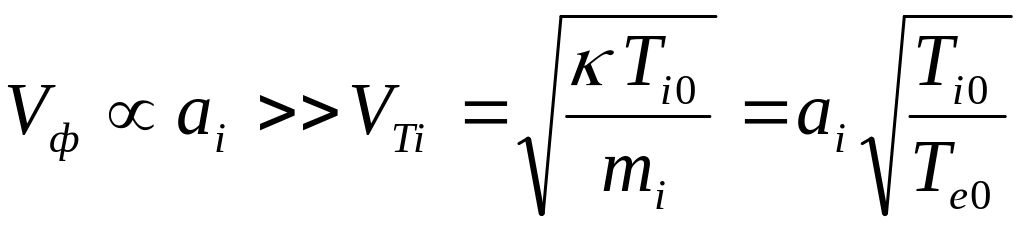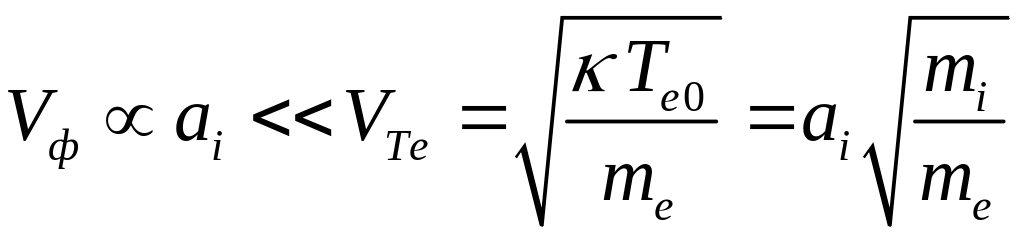Обсудим пренебрежение членом в уравнении движения электронов. Это можно делать при условии, что упорядоченные скорости электронов и ионов являются величинами одного порядка малости. Покажем это. Имеем оценку

С учетом уравнения неразрывности получаем

.

Согласно(14.5) имеем

,

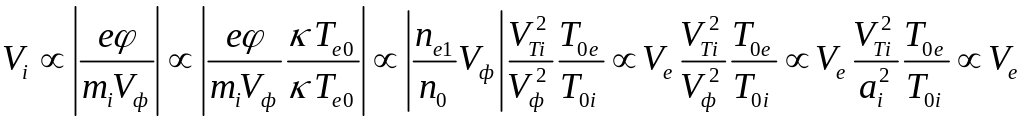где .

Таким образом, имеет место соотношение между скоростями электронной и ионной компонент в ионно-звуковых волнах:

14.2. Нелинейные простые длинноволновые ионно-звуковые воны. Рассмотрим одномерные нелинейные длинноволновые ионно-звуковые возмущения. В такой ситуации хорошо выполняется условие квазинейтральностии и имеется слабое отличие концентрации электронов от концентрации ионов. Для нелинейных одномерных волн уравнение (14.2) в такой ситуации имеет вид

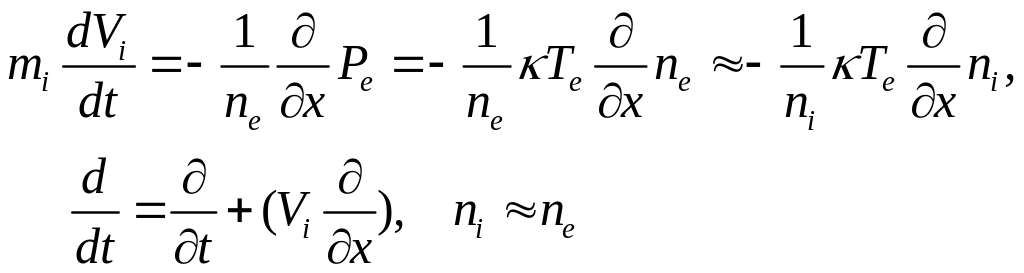. (14.7)

Совместно с уравнением неразрывности

(14.7а)

получили замкнутую систему уравнений в частных производных для двух функций. Если сделать линеаризацию этой системы, то можно убедиться в отсутствии дисперсии (дисперсионное уравнение имеет вид ). Ниже индекс опустим. Найдем частное решение этой системы в виде простой волны (волны Римана):

.

Уравнение неразрывности (14.7а) и уравнение движения(14.7) можно представить в виде

. . (14.8)

Исключив из этой системы , получим соотношение

. (14.9)

Система (14.8), (14.9) приводится к одному уравнению для функции

,или .

Это уравнение можно представить в характеристической форме в виде обыкновенных дифференциальных уравнений ,

которые справедливы на линиях, называемых характеристиками: .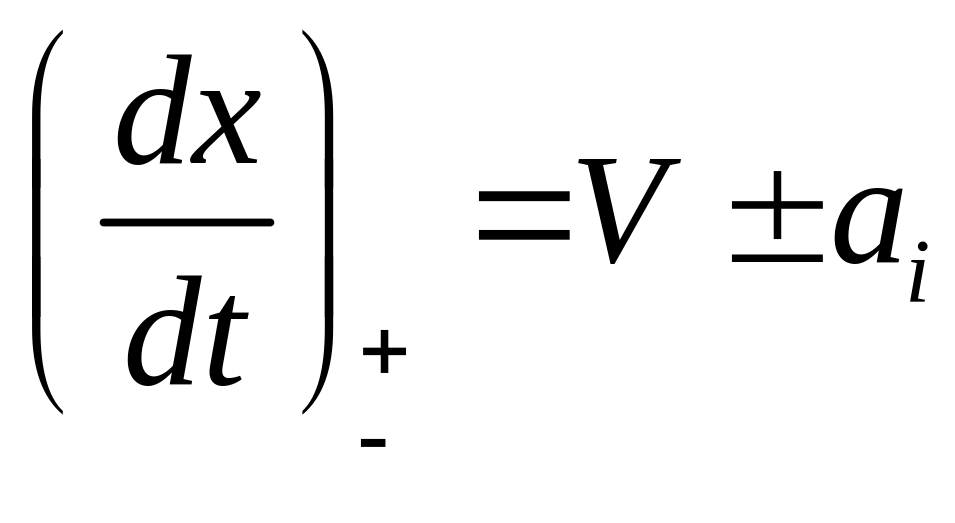

Знаки + и – соответствуют волнам, распространяющимся в сторону соответственно. На характеристиках имеет место представление .

Если вместо функции находить (это преобразование называется преобразованием годографа (изобажения), hodos греческ. - путь), то уравнения для характеристик можно проинтегрировать по времени и получить представление для «пути»:

.

Для нахождения простой волны последнее представление необходимо «обратить» и найти , а затем найти , решив уравнение (14.9):

.

Можно показать, что частное решение в виде простой волны имеет физический смысл в областях, где заканчивается нелинейное взаимодействие волн идущих навстречу друг другу, и реализуется нелинейное распространение одной простой волны в одну сторону.

14.3. Нелинейные стационарные ионно-звуковые волны. Нелинейные ионно- звуковые волны опишем системой уравнений

, (14.10)

,(14.11) , (14.12)

. (14.13)

Из уравнения движения электронной компоненты (14.10) получим представление

.

Ниже ограничимся рассмотрением одномерного процесса, приведя уравнения (14.11) - (14.13) к виду , (14.14) , (14.15)

. (14.16)

Стационарной волной называется волна вида , это волна распространяется с постоянной скоростью в сторону и при этом не изменяет свой «профиль». Исследуем свойства таких волн. Введем обозначения и систему (14.14)-(14.15) представим в виде обыкновенных дифференциальных уравнений

, .

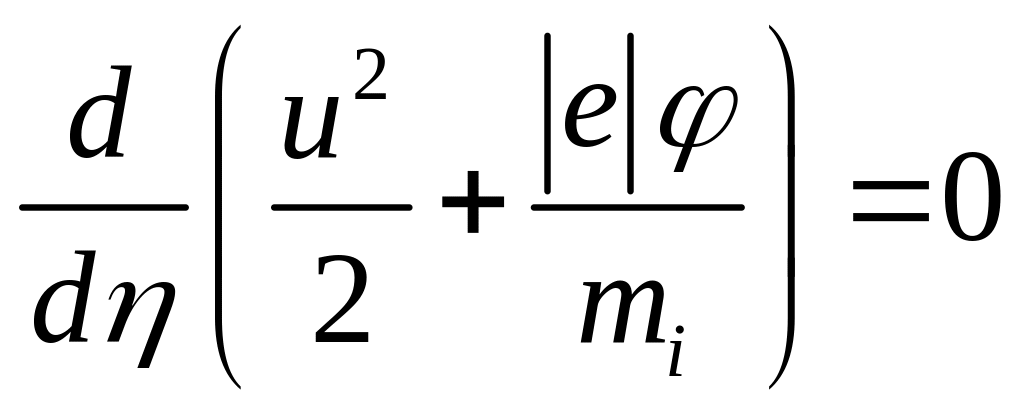Имеем .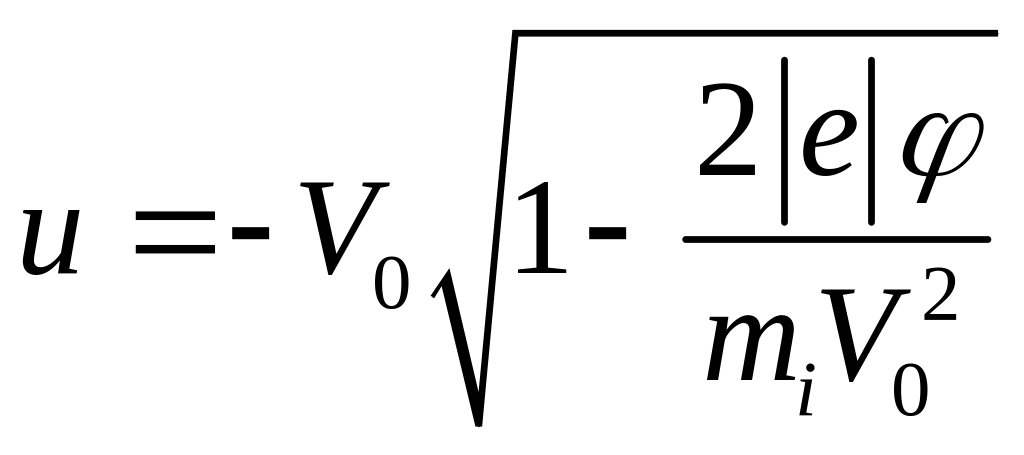

Следствием последних соотношений является представление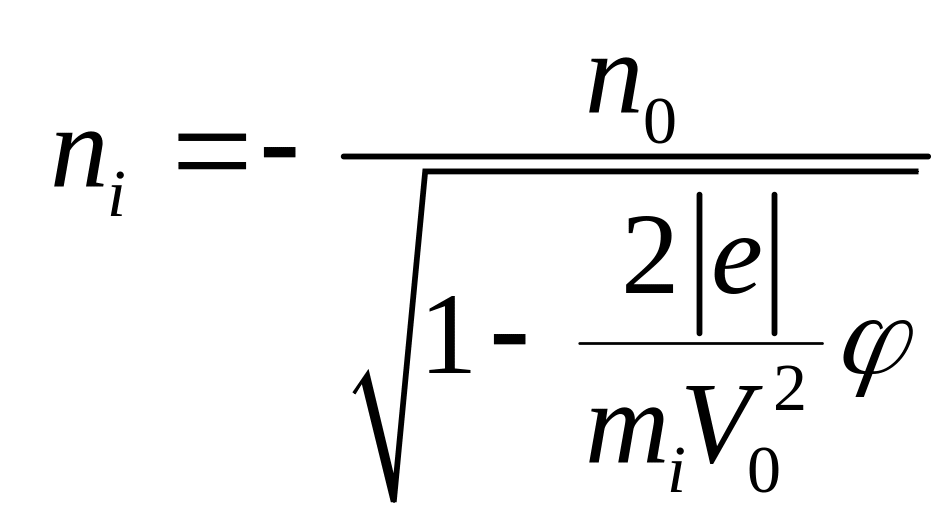 . (14.17)

Следует отметить, что в рамках нашего рассмотрения имеется ограничение на величину потенциала

,

так как при нарушении этого неравенства поля становятся мнимыми величинами.

С учетом представления (14.17) уравнение (14.16) приводится к виду

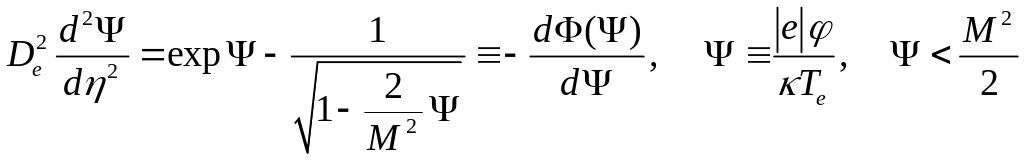, (14.18)

где 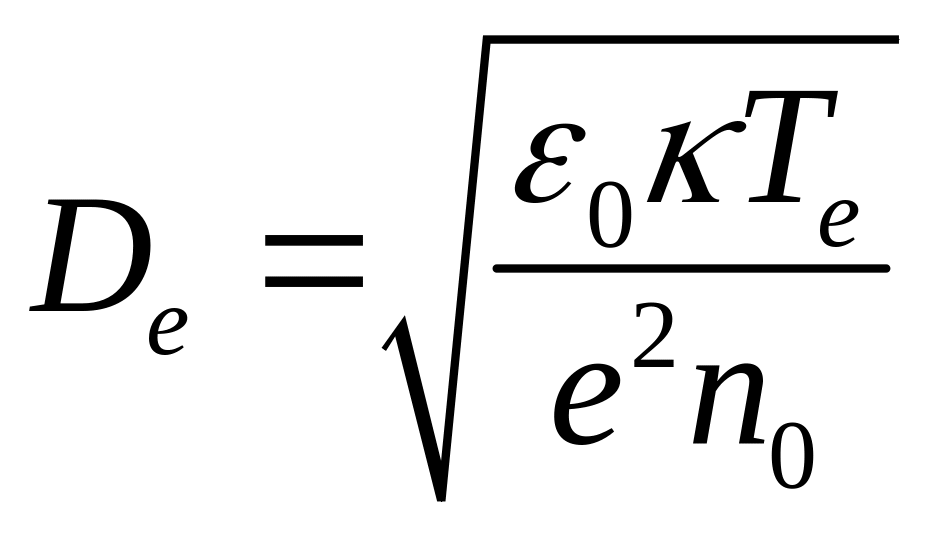- радиус Дебая, - ионно-звуковое число Маха, Для обеспечения вещественности полей в рамках рассматриваемой идеализации имеется ограничение на величину сверху:

. (14.19)

Отметим, что в случае слабой нелинейности допустимо разложение правой части в ряд Тейлора, при этом ограничение (14.19) отсутствует (это соответствует идеализации Кортевега- де Вриза 1895 г. при описании волн в мелком водоеме).

В нашей задаче функция имеет вид.

. (14.20)

Ниже ограничимся рассмотрением случая («сверх ионно- звуковое» течение плазмы), когда функция имеет вид «ямы» а не «горба». Величину константы в (14.20) возьмем такой: , чтобы выполнялось условие . При этом имеем

.

График изображен на Рис. 13.7-13.9.

Уравнение (14.18) является аналогом уравнения движения материальной точки массой в потенциальной «яме» , когда роль координаты играет , а роль времени играет .

Проинтегрируем (14.18), приняв во внимание представление

.

Здесь штрихом обозначена производная по аргументу. Приходим к соотношению, связывающему между собой и

, (14.20.А) при (14.20.Б)

где . Плоскость с координатными осями и называется фазовой плоскостью. Особые точки дифференциального уравнения (14.18) это: седло ( ) и центр ( )На Рис. 13.7-13.9 изображен фазовый портрет – семейство линий при некотором фиксированном значении числа . Стрелочками отмечено направление эволюции при увеличении . Случай соответствует фазовой траектории, проходящей через начало координат . Это соответствует непериодическому уединенному (локализованному) стационарному решению. Оно называется солитоном. Внутри фазовой траектории, описывающей солитон, имеются замкнутые траектории при . Эти фазовые траектории соответствуют периодическим стационарным решениям. Имеются также фазовые траектории, «уходящие» на бесконечность, такие ситуации физически не реализуемы.

Интегрирование (14.20) позволяет найти зависимость

.

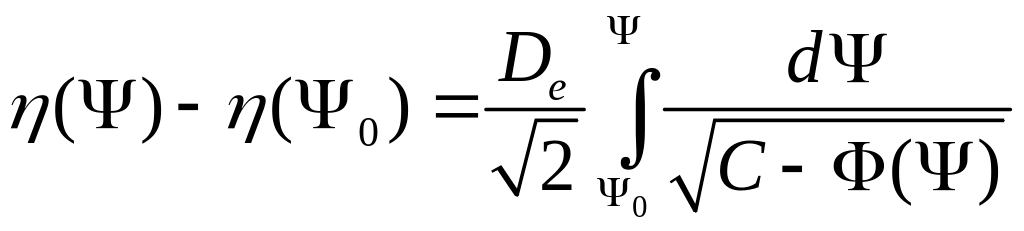Из этого уравнения можно получить нелинейное дисперсионное уравнение. Максимальное значение функции реализуется при выполнении условия (см. (14.20.Б)):

, .

Согласно (14.9) максимально возможное (критическое) значение безразмерного потенциала . При этом фазовая траектория роходит через начало координат и точку на оси абсцисс. В результате имеем уравнение для определения критического значения ионно-звукового числа Маха .

Такая ситуация реализуется в непериодическом решении (солитоне) –см. Рис.13.7. Таким образом, стационарный ионно-звуковой солитон реализуется при выполнении условия .

На Рис.13.7 – 13.9 изображены различные ситуации для случаев .

В случае необходимо уточнять постановку задачи: учитывать дополнительные факторы (существование нестационарного процесса, диссипацию, кинетические эффекты, отражение частиц от потенциального барьера…). В окрестности будет происходить резкое изменение свойств волны. Следует отметить, что ограничение сверху на число типично и для других задач о стационарных волнах в средах с дисперсией при наличии сильной нелинейности. В случае проявления слабой нелинейности имеется ограничение только снизу . На Рис.13.10.Б изображено семейство потенциалов при различных значениях . Заштрихованная область физически не реализуема, там . На Рис.13.7 – Рис.13.10 изображены ситуации, соответствующие трем случаям: . Периодические стационарные волны реализуются во всех ситуациях при . Уединенная волна реализуется только при . Студентам самостоятельно получить нелинейное дисперсионное уравнение.

14.4. Основные положения магнитной гидродинамики (МГД). Исследуем низкочастотные процессы в плазме при наличии однородного внешнего постоянного магнитного поля. Если характерные времена таких движений (например, периоды колебаний) велики по сравнению со временем свободного пробега частиц, то плазма ничем не отличается от обычной жидкости или газа и подобно им описывается уравнениями сплошной среды. Приближением сплошной среды можно пользоваться в том случае, если характерные пространственные масштабы возмущений гораздо больше длинны свободного пробега частиц. Специфика плазмы проявляется во внешнем магнитном поле и связана она с тем, что плазма – хороший проводник электричества. Это обусловлено возбуждением токов индукции, которые совместно с магнитным полем оказывают влияние на проводящую среду. Благодаря медленности процесса существенна роль движения тяжелых частиц – ионов. В таких процессах происходит движение больших масс вещества. Сейчас ограничимся изучением плазмы как единой, сплошной среды, не вникая в рассмотрение движения ее компонент (такое приближение отличается от ситуации, рассмотренной в пункте 14.1, где использовалась идеализация двухкомпонентной среды). Шведский физик Х. Альфвен первым обратил внимание на специфическую роль магнитного поля при движении проводящей среды (в том числе и плазмы). В область применений магнитной гидродинамики входят очень разнообразные объекты – от жидких металлов до солнечной и космической плазмы. Очень широко применяются МГД эффекты для решения прикладных задач (генераторы, бесконтактные динамические расходомеры, измерители скорости, ракетные движители, движители морских судов, насосы…). Магнитная проницаемость сред, о которых идет речь в магнитной гидродинамике, мало отличается от . Система уравнений Максвелла имеет вид

,

где - плотность тока свободных и связанных зарядов в плазме. Материальная связь является обобщенным законом Ома.

14.5. Обобщенный закон Ома для медленных нерелятивистских процессов. Рассмотрение начнем в штрихованной системе координат, движущейся вместе с плазмой. Относительно такой системы плазма неподвижна .

Такая система координат должна быть «локальной» - она в различных точках среды перемещается с различной скоростью и различным ускорением. Ограничимся ниже нерелятивистским приближением

.

Для описания медленных МГД процессов (критерии медленности будут даны ниже) используем закон Ома в очень простой форме , (14.1)

где - электропроводность плазы. Отметим особенности материальной связи (14.1) в движущейся системе координат:

• линейность,

• локальность (связь алгебраическая),

• изотропность ( - скаляр, а не тензор).

Тот факт, что - это линейное соотношение и уравнения Максвелла – линейные, не должно создавать иллюзий, что в магнитной гидродинамике не будут учтены нелинейные эффекты. Дело в том, что в (14.1) необходимо сделать преобразование перехода в лабораторную систему координат (это приведет к нарушению линейности). Для нерелятивистских процессов с точностью до членов порядка имеем представления , ,

- внешнее магнитное поле (ниже будем считать ). Для плотностей токов имеем представления , ,

где - заряд, концентрация, скорость - ой компоненты в плазме. С точностью до членов порядка имеем представления , ,

где - плотность электрических зарядов. Ниже ограничимся приближением слабого нарушения электронейтральности: и получим обобщенный закон Ома для медленных процессов в плазме . (14.2)

Это представление можно получить на основе преобразования Лоренца (см. раздел 12.7) 4-х вектора плотности тока : , (14.2.А)

где - тензор Лоренца, в соотношении (14.2.А) следует ограничиться учетом членов порядка .

Выясним, к каким ограничением приводит, использованное неравенство . С этой целью сделаем оценку полей, считая, что плазма состоит из электронов и положительных ионов

, .

Это приводит к неравенству, характеризующему слабое нарушение электонейтральности плазмы

,

где параметр в медленных процессах является величиной порядка единицы.

Закон Ома (14.2) содержит произведение неизвестных функций . Тем самым, здесь имеет место учет нелинейности. Тот факт, что в закон Ома вошла новая неизвестная функция (упорядоченная скорость плазмы), делает систему уравнений Максвелла совместно с законом Ома незамкнутой системой уравнений. Возникает необходимость введения в рассмотрение дополнительных уравнений, содержащих (это будут уравнения динамики плазмы).

14.6. Уравнения динамики плазмы. Перейдем к дальнейшему замыканию системы уравнений магнитной гидродинамики, привлекая уравнения динамики плазмы. Как уже отмечалось выше, плазму будем рассматривать как единый «коллектив», не различая отдельные компоненты.

1). Уравнение движения плазмы

, (14.3)

где - плотность и скорость плазмы, - плотность электрических зарядов, . В уравнении (14.3) нет слагаемого, учитывающего упругие соударения между частицами плазмы, так как такие соударения не приводят к изменению полного импульса системы. В результате соударений происходит обмен импульсами между отдельными частицами и различными компонентами плазмы. В уравнении движения (14.3) не учитывается диссипация за счет влияния вязкости. Нелинейность содержится в левой части (14.3) и в членах правой части. В уравнение движения входят две новые неизвестные функции и . Необходимо добавить дополнительные уравнения для описания этих функций (уравнение неразрывности и уравнение состояния).

2). Уравнение неразрывности (закон сохранения массы) можно использовать в двух эквивалентных формах

(14.4)

отметим наличие нелинейности в (14.4).

3). Уравнение состояния для давления

, либо ,

где - температура и энтропия. Простейшим видом уравнения состояния является уравнение состояния совершенного газа ,

где - газовая постоянная.

4). Уравнение для плотности внутренней энергии используем в виде

,

где - энтальпия (тепловая функция) и плотность работы сил давления при изменении объема плазмы, - работа сил давления, - учет влияния потока тепла , - диссипация за счет электропроводности плазмы. Простейший вид связи и , .это закон Фурье – Ньютона:

,

где - коэффициент теплопроводности. В случае волн малой амплитуды используется линейное приближение: считается, что не зависит от . Для описания сильных нелинейных тепловых эффектов учет такой зависимости необходим. Примером может служить эволюция огненного шара при ядерном взрыве.

5). Уравнение состояния для плотности внутренней энергии .

Такое локальное соотношение предполагает отсутствие «релаксации» - задержки во времени при установлении колебательной и вращательной долей энергии. При описании МГД процессов широко используется приближение совершенного газа ,

где - удельная теплоемкость при постоянном удельном объеме .

В случае пренебрежения диссипацией за счет вязкости и теплопроводности, и при использовании модели совершенного газа будем пользоваться линеаризованной системой уравнений МГД без сторонних источников: ,

(во втором уравнении сделано пренебрежение током смещения , условие такого пренебрежения будет обсуждаться ниже),

, , , , ,

где - линейное приближение скорости звука, ,диссипация за счет конечной электропроводности учтена.

В задачах о МГД волнах источниками полей могут быть заданные функции в системе уравнений Максвелла и в системе уравнений динамики плазмы (источник массы, источник импульса, источник энергии).