13.2. Уравнения электродинамики быстропеременных процессов в плазме. Диэлектрическая проницаемость однородной изотропной плазмы.

1). Электромагнитные поля в плазме могут создаваться как внешними источниками, так и внутренним неоднородным и нестационарным распределением зарядов. В плазме возникает самосогласованное взаимодействие заряженных частиц и поля. Основой системы уравнений, описывающей процессы в плазме, являются уравнения Максвелла (сами по себе эти уравнения не замкнуты и они должны быть дополнены уравнениями динамики)

Эту систему необходимо дополнить уравнениями, описывающими материальные связи в плазме. В качестве таких дополнительных уравнений можно использовать уравнения динамики плазмы, как сплошной среды. Интересуясь сейчас свойствами быстропеременных полей в плазме, ограничимся следующим приближением. Ионы, как тяжелые частицы, будем считать неподвижными. Электронную компоненту опишем системой уравнений динамики (уравнений сплошной среды).

,

это уравнение движения. Здесь - давление электронной компоненты, - частота упругих соударений электронов с частицами других сортов (ионами и нейтральными частицами), , - внешнее магнитное поле, . Уравнение движения – это нелинейное уравнение в частных производных.

Простейшее уравнение состояния для давления, это уравнение состояния совершенного газа

,

где - постоянная Больцмана. Ниже пренебрежем влиянием изменения температуры, и уравнение состояния для давления используем в виде

. .

Здесь и ниже индексом нуль будем отмечать однородные невозмущенные значения полей.

Концентрация и скорость связаны уравнением неразрывности

.

В невозмущенном состоянии электронную компоненту будем считать неподвижной и однородной. Поля в невозмущенном состоянии обозначаем индексом ноль. Интересуясь в этом разделе полями малой амплитуды, произведем линеаризацию:

,

,

где - частота столкновений электронов с ионами и нейтральными частицами.

2). Диэлектрическая проницаемость однородной изотропной плазмы. Пусть сторонние источники отсутствуют. Рассмотрим распространение плоских монохроматических поперечных волн в плазме, когда поля изменяются по закону

.

При этом имеют место соотношения

где экспоненциальный множитель опущен. Дифференциальные уравнения в частных производных с постоянными коэффициентами превратятся в алгебраические уравнения для комплексных амплитуд. Уравнения Максвелла примут вид

, , .

Уравнение движения для поперечных волн в изотропной плазме принимает вид

.

Следует подчеркнуть, что в уравнение движения для поперечных волн не входит сила газового давления, так как она параллельна вектору . В рассматриваемой здесь идеализации конечность температуры электронной компоненты не влияет на поперечный волновой процесс. Из уравнения непрерывности для поперечной волны следует, что - не происходит возмущения концентрации электронов. Поэтому . Для поперечных волн уравнение неразрывности не участвует в описании процесса. Получили систему четырех однородных алгебраических уравнений для четырех комплексных амплитуд . Условие разрешимости системы – равенство нулю детерминанта (это характеристическое уравнение):

, ,

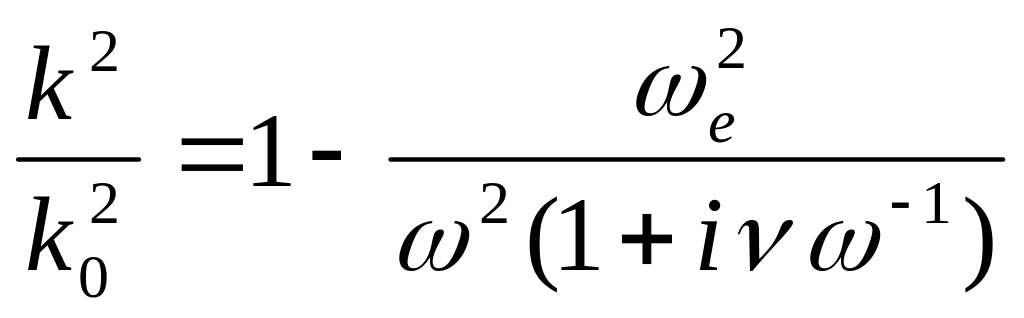где 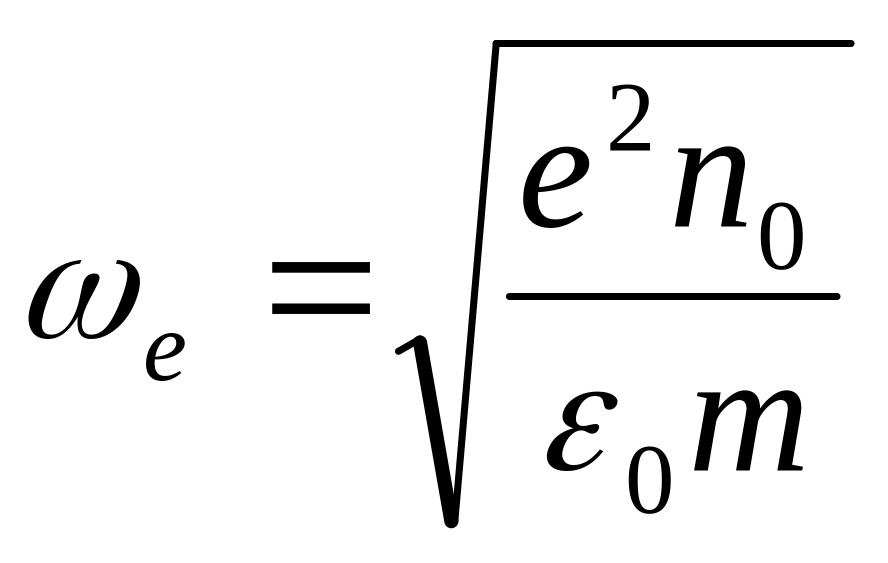- электронная плазменная частота - показатель преломления (не путать с концентрацией). Дисперсионное уравнение позволяет найти .

Из системы уравнений

следует представление . Поэтому из дисперсионного уравнения получается представление для показателя преломления и для относительной комплексной диэлектрической проницаемости . Таким образом, имеем

.

Зависимость от - это признак наличия временной дисперсии, а зависимость от волнового числа - это признак наличия пространственной дисперсии. В рассматриваемой ситуации Волновой поперечный процесс (ситуация, когда ) в изотропной плазме не обладает пространственной дисперсией, так как .

При имеет место предельный переход к вакууму: .

Воспользуемся соотношением

Имеющим Фурье – аналог .

Выражение для комплексной функции представим в виде

Рассмотрим два предельных случая

А). Пусть , тогда

случай соответствует отсутствию потерь, электропроводность (в рассмотренном приближении единственный механизм диссипации это потеря энергии у электронной компоненты при упругих соударениях с ионами и нейтральными частицами). Если при и плазменная частота удовлетворяет условию , то обращается в нуль при (Рис.13.1а). Если же , не обращается в нуль (Рис.13.1б), причем как в случае 11.1а и 11.1б имеет место универсальный предельный переход к вакууму: при .

Выясним основные дисперсионные закономерности при :

,

Имеет место свойство: при . На Рис. 13.2 показана зависимость фазовой (а) и групповой (б) скоростей от частоты. В области скорости и становятся чисто мнимыми (это область непрозрачности плазмы).

Б). Если то получим приближенные формулы

что соответствует отсутствию временной дисперсии. В рамках такого приближения нельзя переходить к пределу при конечных значениях . Нельзя так же делать предельный переход , так как существует ограничение .

Выясним условия применимости линеаризации

,

из уравнения следует оценочное соотношение .

В уравнении движения при линеаризации использовалось условие

.

Не трудно убедиться, что приведенные выше неравенства выполняются при условии

.

13.3. Дебаевское экранирование. В следующем разделе понадобится понятие радиус Дебая. Оно уже обсуждалось раньше в разделе 13.1 на основе приближенных оценочных исследований. Обсудим сейчас это понятие подробнее. Характерная длина, описывающая пространственный масштаб экранирования, впервые была введена Дебаем и Хюккелем (1923 г.) при рассмотрении процессов в сильных электролитах. В дальнейшем это понятие было перенесено в электродинамику плазмы. Рассмотрим идеализированную электростатическую ситуацию (строго говоря, это выходит за рамки данного раздела 13, так как в этом разделе рассматриваются быстропеременные процессы).

Пусть в начале координат закреплен точечный заряд , и он окружен плазмой. Будем рассматривать плазму как две взаимодействующие сплошные среды. Требуется найти установившееся статическое распределение потенциала поля. Потенциал удовлетворяет уравнению

,

где штрихом отмечены возмущенные значения полей, - заряд электрона. Для статической ситуации , уравнения движения электронной и ионной компонент имеют вид нелинейных уравнений

. (13.3.А)

Для описания давления используем уравнение состояния совершенного газа

.

Здесь - постоянная Больцмана. Ниже ограничимся идеализацией . Так как в электростатике , то нелинейные уравнения движения принимают вид

.

Получаем нелинейные представления для концентраций

.

Уравнение (13.3А) принимает вид неоднородного нелинейного уравнения

. (13.3.Б)

Построим решение , удовлетворяющее граничным условиям

.

Для описания процессов в плазме наибольший интерес представляет ситуация, когда потенциальная энергия взаимодействия заряженных частиц мала по сравнению с их кинетической энергией (это есть условие газового приближения):

.

В такой ситуации уравнение (13.3.Б) становится приближенно линейным однородным уравнением. Так как невозмущенное состояние однородно и заряд - точечный, то будет иметь место сферическая симметрия

, ,

где 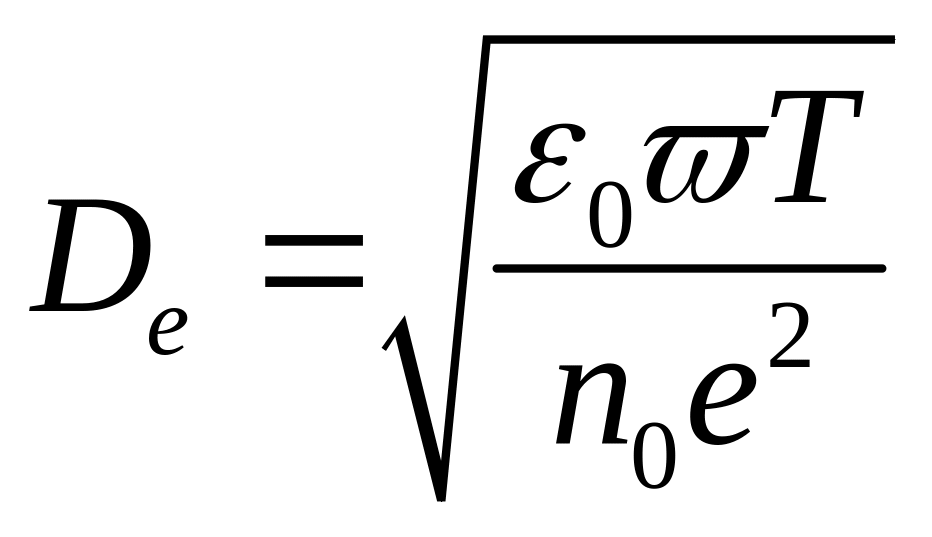- введенный ранее радиус экранирования Дебая. .

Постоянную выбираем из требования предельного перехода к кулоновскому полю при (строго говоря, в полученном приближенном решении нельзя делать переход к случаю так как при этом нарушается неравенство ): .

Потенциал в области экспоненциально мал. Здесь поле заряда экранировано полем зарядов противоположного знака. Это обеспечивает электронейтральность плазмы при . Электронейтральность нарушается в области .

Полученное таким образом приближенное решение пригодно на больших расстояниях, когда и это решение применимо в малой окрестности около заряженной частицы. На промежуточных расстояниях это приближенное решение не пригодно.

13.4. Продольные плазменные колебания в холодной плазме. Нелинейные стационарные продольные плазменные волны в холодной плазме. Продольные плазменные волны малой амплитуды в горячей плазме.

1). Продольные плазменные колебания в холодной плазме. В случае продольного процесса рассмотрим быстропеременные поля, считая ионную компоненту неподвижной. Закон Кулона возьмем в виде

где - невозмущенная концентрация электронной компоненты плазмы, - возмущенное значение ее. В случае полей малой амплитуды , используем уравнение неразрывности

и уравнение движения в линеаризованном виде (ограничимся сейчас приближением холодной изотропной плазмы: , без учета влияния столкновений ).

Применяя операцию к этому уравнению, и учитывая закон Кулона, получим уравнение для нахождения .

Решение этого уравнения описывает гармонический процесс с плазменной частотой

.

Решение имеет специфический вид произведения двух функций, каждая из которых зависит только от одного аргумента. Это не волновое, а колебательное явление (отсутствует процесс распространения), описанный Ленгмюром (1926 г.). Эти колебания называют плазменными, или ленгмюровскими. Иногда их называют электростатическими, так как электрическое поле потенциально: . Однако, на самом деле эти колебания не являются статическими, так как . Для плоских монохроматических волн (Фурье – образов полей) получается дисперсионное уравнение, в которое не входит волновое число поэтому частота не зависит от волнового числа :

.

Поэтому групповая скорость равна нулю

.

Описанное плазменное колебание – это предельный случай волнового процесса при .

Рассмотрим уравнение Кулона в виде

,

которое для Фурье – образа дает , последнее справедливо, так как для продольной волны . Следовательно, , . Значит, для продольных полей имеет место свойство

.

Этим свойством обладают не только продольные колебания, но и волновые продольные поля в изотропной плазме.

2). Нелинейные стационарные продольные плазменные волны в холодной плазме. Нелинейные одномерные плазменные волны в холодной плазме опишем системой уравнений

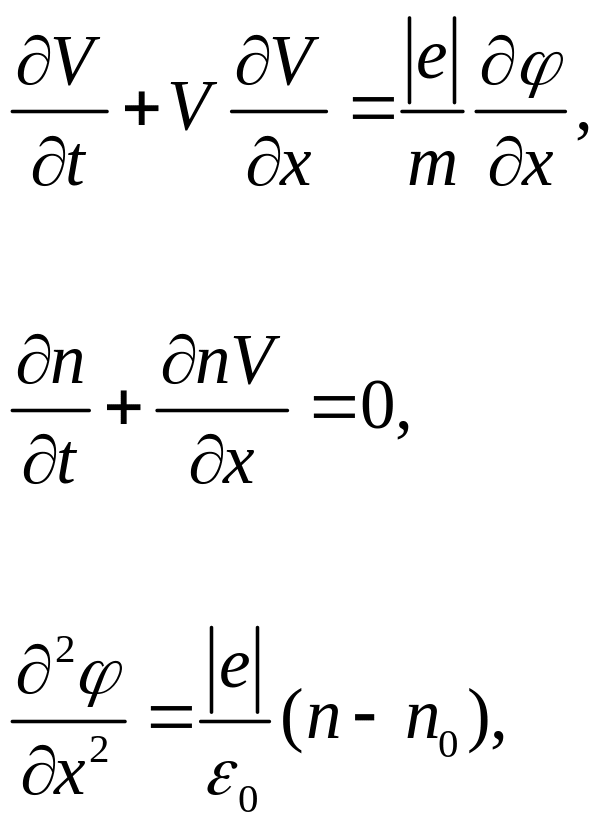
Рассмотрим стационарную волну – волну распространяющуюся с постоянной скоростью и сохраняющую при этом вид своего профиля. В такой ситуации все поля зависят от одной переменной . Считаем, что в невозмущенном состоянии имеет место представление:

.

Получаем соотношение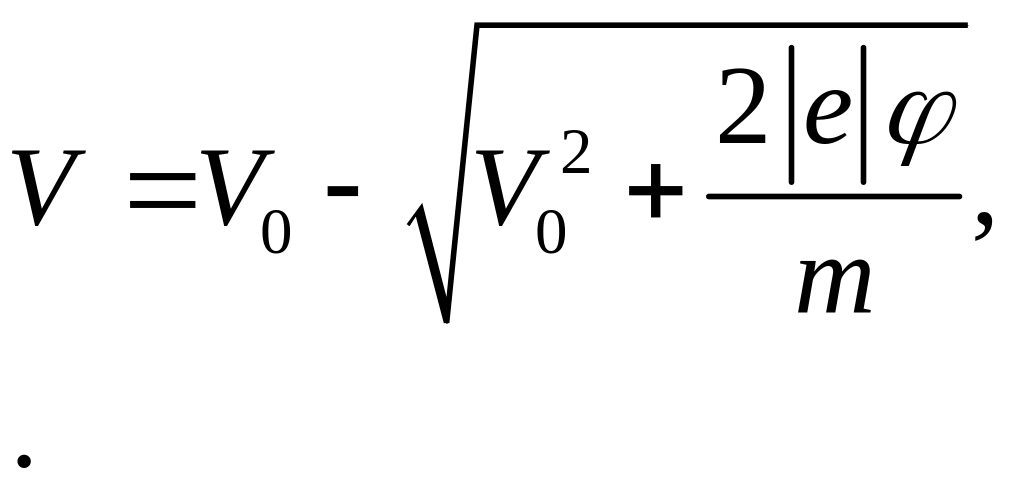

Из уравнения неразрывности следует 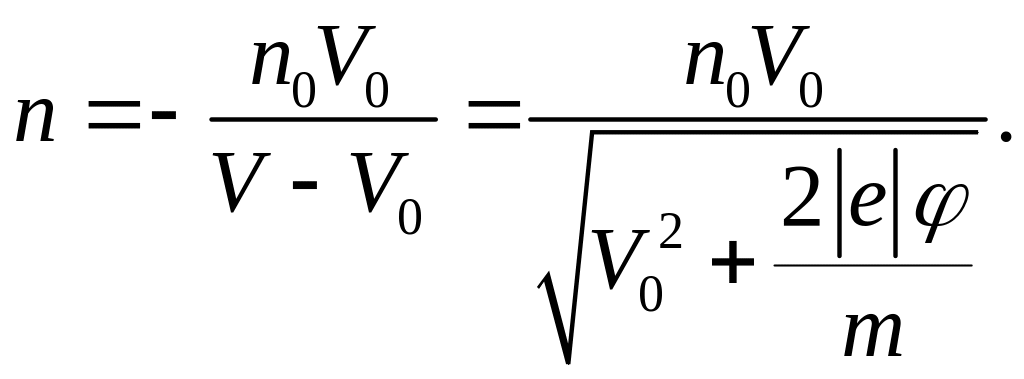(13.5.А)

Для того, чтобы обеспечить вещественность полей необходимо выполнение ограничения на потенциал снизу

.

Следует отметить, что ограничение на амплитуду поля типично для задач, в которых учитывается влияние сильной нелинейности.

Использование соотношения (13.5.А) позволяет представить уравнение Пуассона в виде нелинейного обыкновенного дифференциального уравнения второго порядка

, (13.5.Б)

где .

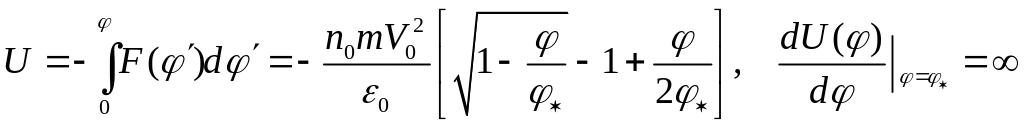Постоянная интегрирования выбрана таким образом, чтобы . График зависимости изображен на Рис. 13.5. В заштрихованной области поля становятся комплексными, такая ситуация физически не реализуется. При выполнении условия необходим учет дополнительных факторов при постановке задачи (например, учет отражения электронов от потенциального горба). В области происходит резкое изменение свойств полей. Уравнение (13.6) является аналогом уравнения движения материальной точки единичной массы в потенциальной яме , - аналог координаты, - аналог времени. Уравнение (13.6) можно проинтегрировать, приняв во внимание соотношение , где штрихом обозначена производная по аргументу. В результате получим

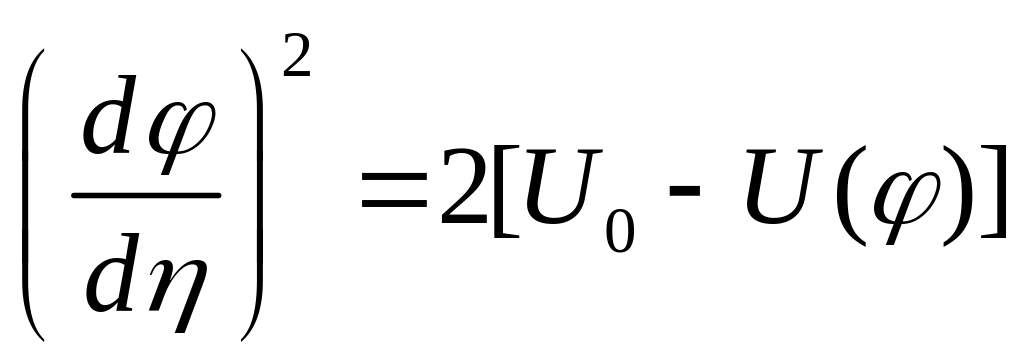. (13.6)

Условие экстремума функции имеет вид .

Параметр задает амплитуду волны. Уравнение(13.6) дает связь между потенциалом и производной .

Интегрирование позволяет найти представление :

.

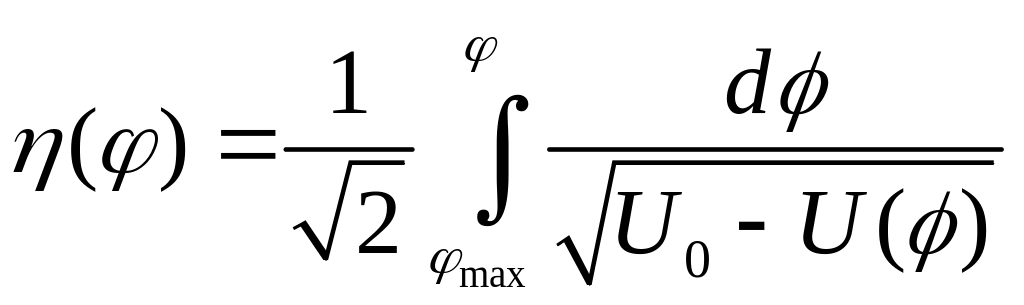Функции - периодические функции Якоби – см. Рис.13.1.б.

В плазменной волне происходит образование стационарного периодического режима только для волн не слишком большой амплитуды: . В случае нарушения этого условия необходимо уточнение модели процесса.

Нелинейное дисперсионное уравнение (условие существования периодического решения) имеет вид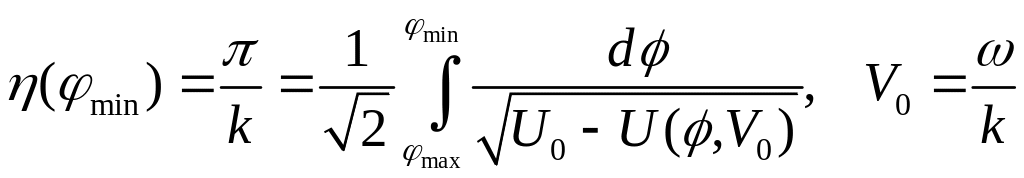

В линейном приближении частота не зависит от волнового числа (этот факт уже был зафиксирован выше) ,

поэтому групповая скорость в этом приближении равна нулю

,

И волновой процесс вырождается в процесс колебательный. Следует подчеркнуть, что рассматриваемая ситуация достаточно специфическая. При уменьшении амплитуды периодический волновой процесс вырождается в колебательный процесс.

3). Продольные плазменные волны малой амплитуды в горячей плазме. Пренебрежение хаотическим тепловым движением электронов ( ), как показано выше, приводит к тому, что в изотропной плазме линейный продольный волновой процесс вырождается в процесс колебательный. Выясним влияние конечности температуры на продольный волновой процесс. Используем линеаризованные уравнения движения и неразрывности

.

В таком приближении не учитывается сила трения за счет упругих соударений электронов с ионами и нейтральными частицами. Так как процесс продольный, то и для описания электрического поля достаточно использовать уравнение Кулона .

Система этих трех уравнений не замкнута, необходимо добавить уравнение, описывающее давление (уравнение состояния для давления). Ограничимся здесь простейшим уравнением состояния совершенного газа .

Множитель 3 в формуле для учитывает упорядоченность движения электронов в возмущениях плазмы. Более строго учет этого множителя доказывается в кинетической теории плазмы. Пренебрегая возмущениями температуры, линеаризованное уравнение состояния получим в виде

.

Получим дисперсионное уравнение. Это можно сделать, например, исключив из системы : Уравнение для Фурье - образа имеет вид .

Дисперсионное уравнение приводится к форме

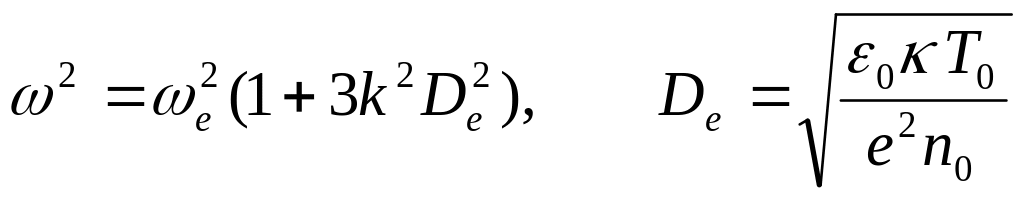,(13.5.В)либо .

Последняя формула дает представление для в случае продольных волн:

.

Учет влияния конечности температуры электронной компоненты приводит к наличию пространственной дисперсии у продольного процесса. Признаком этого является зависимость от . В отличие от ситуации, анализированной в пункте1) данного раздела, возникает связь и фазовая скорость описывается соотношением

Групповая скорость отлична от нуля (колебательный процесс превращается в волновой)

.

Для продольной волны справедливо свойство . Напомним, что для волны поперечной было: и конечность температуры электронной компоненты не влияла на дисперсионные свойства плазмы.

Переход к приближению холодной плазмы осуществляется при выполнении условия

или .

Это случай длинноволнового приближения.

Более точное кинетическое описание продольной волны дает дисперсионное уравнение при : .

Кинетическая теория подтверждает правильность сделанного выше допущения . Отметим, что кинетическое описание дает дисперсионное уравнение не в алгебраической форме. В такой более точной теории, даже без учета столкновений (бесстолкновительная плазма) функция является комплексной. Это соответствует затуханию продольной волны. Такое затухание называется затуханием Ландау (1946 г.), оно обусловлено тем, что происходит резонансное взаимодействие частиц с полем продольной волны. Взаимодействие особо эффективно в том случае, когда фазовая скорость волны близка к проекции скорости частицы на направление волнового вектора. Медленные электроны (их гораздо больше, чем быстрых электронов) «отбирают» у электрической волны больше энергии, чем быстрые «отдают» ее волне. Под действием электрического поля распределение электронов по скоростям изменяется так, что оно отличается от максвелловского. Этого эффекта нет в приближении сплошной среды – бесстолкновительное затухание это кинетическое явление.

Из за большого различия масс ионов и электронов, влияние движения тяжелых частиц (ионов) на быстрый (высокочастотный) процесс оказывается слабым, если . Ниже будет показано, что при влияние ионов становится существенным в области низких частот.

13.5. Диффузия плазмы. Рассмотрим достаточно медленный процесс при наличии частых столкновений электронов с тяжелыми частицами (ионами и нейтральными частицами):

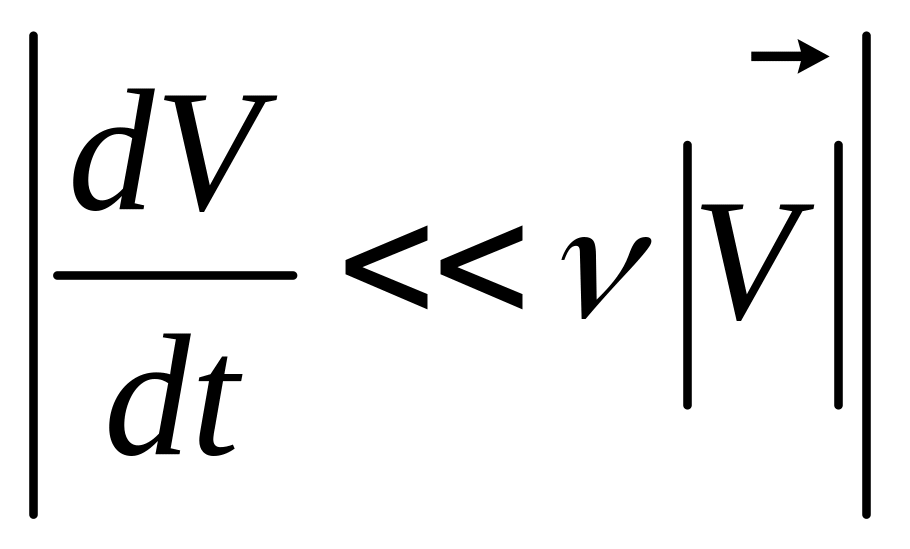
и пренебрежем инерционным членом в уравнении движения электронной компоненты

Получаем соотношение

,

где - подвижность, - коэффициент диффузии, - поток электронной компоненты плазмы. Имеет место соотношение Эйнштейна, дающего связь между коэффициентами и

.

В случае выполнения неравенства имеет место диффузионный процесс. Он описывается законом Фика .

В этом приближении существует поток электронов из области большей их концентрации в область меньшей концентрации. Уравнение неразрывности для диффузии в неоднородной среде принимает вид уравнения диффузии в неоднородной среде .

При , имеем уравнение диффузии .

Если неравенство нарушается, то ситуация усложняется за счет влияния электромагнитного взаимодействия заряженных компонент.

13.6. Диффузия в слое плазмы, ограниченном стенками. Рассмотрим эволюцию одномерного пространственного распределения плазмы между двумя стенками в случае . Будем считать, что на стенках концентрация обращается в ноль. Уравнение диффузии имеет вид

.

С такими граничными условиями это уравнение имеет бесконечно много решений. Одно из них (самая низкая мода, или нулевая мода) представляется в виде произведения двух функций

.

Уравнению диффузии можно придать вид

.

Получаем следующее представление

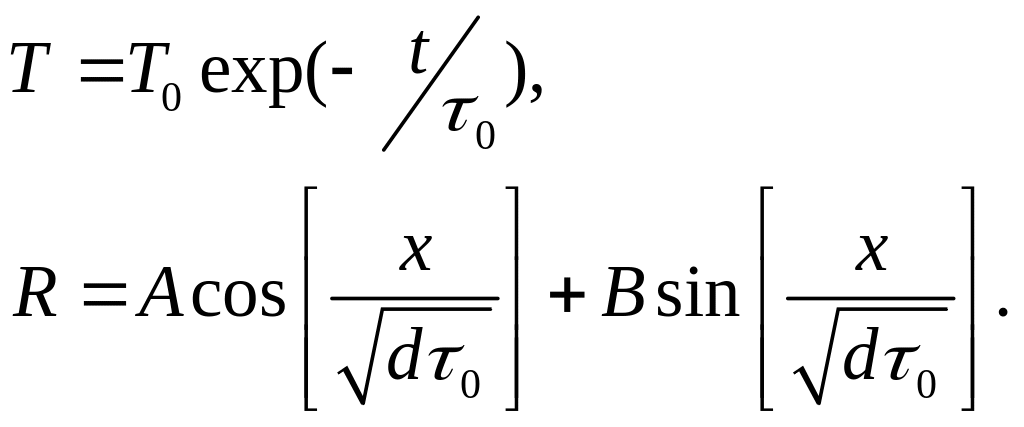
Для решения с одним максимумом у функции при , из граничных условий получаем значения двух констант 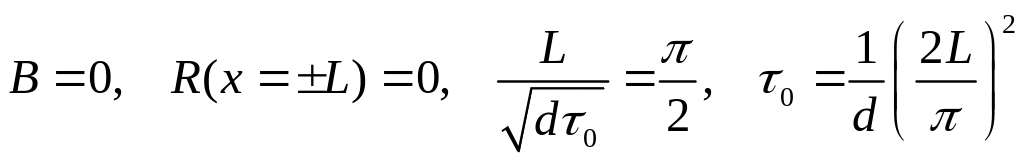. Это соответствует описанию наинизшей (нулевой) моде:

, .

Если известно начальное распределение концентрации , , то можно построить решение нестационарной задачи методом разделения переменных. Пусть начальное возмущение такое, что допустимо разложение в ряд Фурье:

.

Правая часть этого представления обращается в ноль при . Решение нестационарной задачи можно построить в виде

.

Подстановка этого представления в уравнение диффузии и приравнивание коэффициентов при и дает представление для масштаба затухания -ой и -ой моды

.

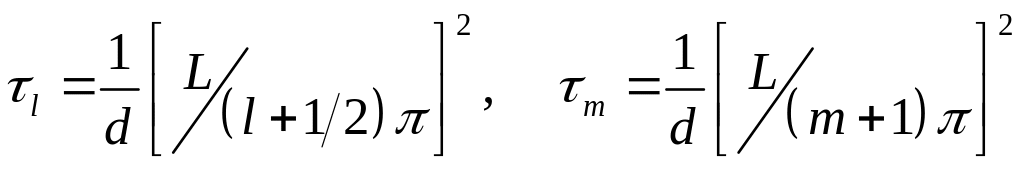Гармоники с большими номерами затухают быстрее, чем гармоники с меньшими номерами. Постепенно начальное распределение превратится в нулевую моду. Потом будет происходить уменьшение ее амплитуды, в то время, как форма распределения будет оставаться неизменной.

13.7. Действие статического источника ионизации в плазменном слое. В экспериментальных установках возможно поддержание установившегося стационарного состояния путем непрерывной дополнительной ионизации или инжекции плазмы. При этом компенсируются потери за счет диффузии. Рассмотрение такой ситуации возможно при добавлении в уравнение диффузии дополнительного члена , описывающего источник:

.

В установившемся состоянии и возникает задача о решении уравнения Пуассона со сторонним источником. Рассмотрим ситуацию когда .

Ситуация №1. Если источник локализован в плоскости, и он действует в слое , то при имеем уравнение .

Граничные условия возьмем в виде . Решение такой задачи имеет представление

.

В точке расположения - образного источника происходит скачок производной функции .

Ситуация №2. Если источник локализован на оси плазменного цилиндра радиуса , то

везде, кроме точки будем иметь уравнение

.

Граничное условие возьмем в виде .Получаем представление

.

Благодаря чрезмерной идеализации постановки задачи (источник бесконечно тонкий) имеется обращение концентрации в бесконечность при .

13.8. Влияние внешнего магнитного поля, анизотропия плазмы. Исследуем влияние постоянного, однородного внешнего магнитного поля на распространение плоских монохроматических волн малой амплитуды (линейное приближение) в холодной ( ), бесстолкновительной плазме ( ), считая ионы неподвижными (высокочастотное приближение). Ниже будет показано, что наличие внешнего магнитного поля делает плазму анизотропной средой.

Система уравнений Максвелла

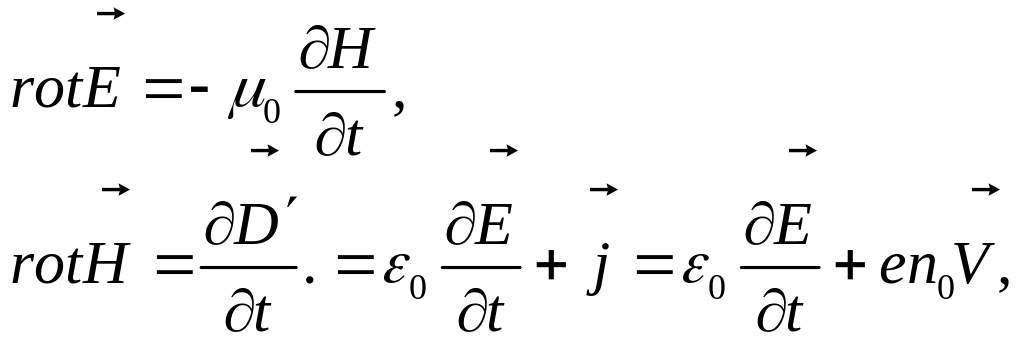
Для Фурье – образов получим связь .

В случае линейных волн, распространяющихся в однородной среде, сводится к векторному алгебраическому уравнению для Фурье – образа

(13.2) . (13.3)

Для того, чтобы получить дисперсионное уравнение, описывающее электродинамические свойства плазмы, необходимо установить связь между и . Уравнение движения, при пренебрежении упругими соударениями и при использовании идеализации холодной плазмы, для Фурье – образов полей имеет вид (индекс у вектора скорости электронов опустим)

, .

Проекции этого уравнения на оси и :

, , .

Отсюда получаем представления

, (13.4)

. (13.5)

- циклотронная частота электронов (частота гирорезонанса электронов).

Ограничимся исследованием двух частных случаев: 1). Поперечное распространение волн и 2). Продольное распространение волн .

1). Поперечное распространение волн , (Рис.13.3). Представим электрическое поле в виде суммы продольной и поперечной компонент , здесь . Магнитное поле не оказывает влияния на движение электронов в случае и , поэтому такая волна называется обыкновенной. В рассматриваемой ситуации . В этом случае получается известный результат (выпишем его с учетом соударений)

.

В случае волна называется необыкновенной.

Условие разрешимости алгебраической системы (13.3)-(13.5) дает дисперсионное уравнение для описания необыкновенной волны.

,

где - верхнегибридная частота. Решение дисперсионного уравнения для волны необыкновенной можно представит в виде

.

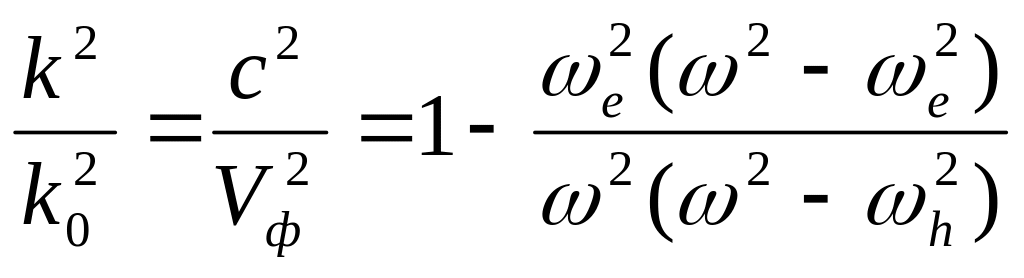2. Продольное распространение волн (Рис.13.4). Если , то это соответствует продольному колебанию и дисперсионное уравнение имеет вид

, или .

Если , то в этом случае поле лежит в плоскости, перпендикулярной волновому вектору: . Соотношения (13.4) и (13.5) остаются применимыми в этой ситуации. Так как при продольном распространении волны , то уравнение (13.2)принимает вид

,

.

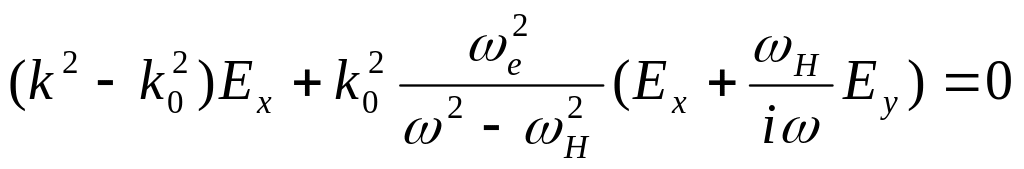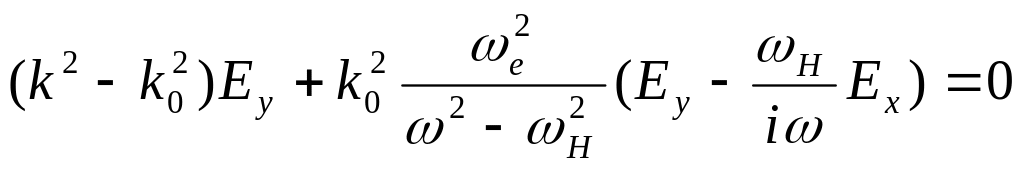Дисперсионное уравнение дает решение в виде

.

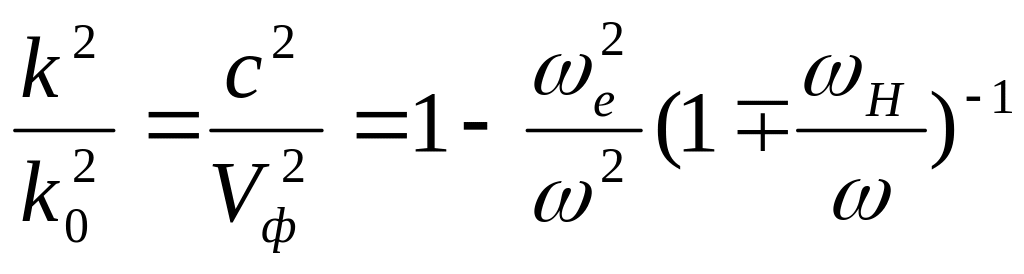Знаки относятся к волнам правой и левой поляризации. Вектор в волне правой поляризации вращается по часовой стрелке, если смотреть по направлению вектора . В волне левой поляризации вращение происходит в противоположную сторону. Эти две волны распространяются с различными скоростями. Это приводит к фарадееву вращению плоскости поляризации.

В случае произвольного угла между векторами и свойства плазмы становятся еще более сложными, чем в рассмотренных двух предельных случаях.

13.9. Диффузия слабоионизированной плазмы поперек магнитного поля. Одной из проблем реализации управляемого термоядерного синтеза является создание условий, препятствующих попаданию плазмы на стенки установки за счет удержание плазмы магнитным полем. Исследуем диффузию слабоионизированной плазмы, находящейся в постоянном однородном магнитном поле . Это поле не влияет на движение заряженных частиц вдоль . Поэтому в продольном направлении потоки частиц будут иметь вид

.

В отличие от предыдущего исследования, сейчас рассмотрим эволюцию как электронной, так и ионной компонент. Если столкновения заряженных частиц с нейтральными частицами отсутствуют, то диффузия поперек магнитного поля не происходит. Исследуем сейчас ситуацию, когда роль столкновений существенна и допустимо пренебрежение инерцией заряженных частиц. Уравнения движения электронов и ионов возьмем в виде (индексы и опустим)

.

Используя проекции этих уравнений на оси и , получим соотношения

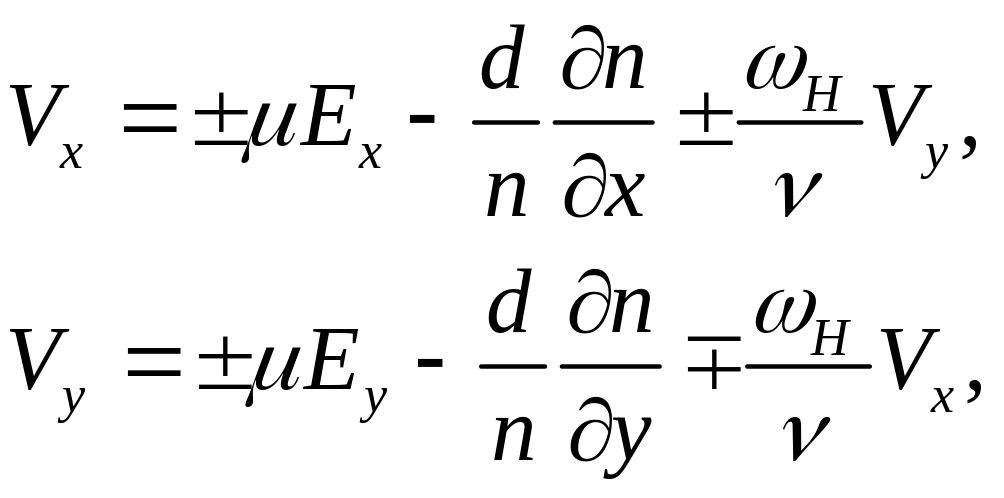
которые преобразуются в представления для поперечной компоненты вектора скорости, которая и характеризует поперечную диффузию:

,

где введены обозначения

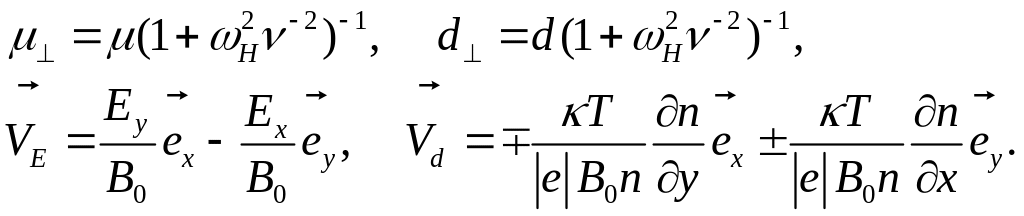
- скорость поперечного дрейфа за счет подвижности и диффузии в направлении векторов и .

- скорость диамагнитного дрейфа.

Сильное влияние магнитного поля на дрейф происходит при условии . При этом имеет место свойство: (напомним, что ).

Отметим, что диффузионные процессы относятся к разряду достаточно медленных процессов, когда допустимо пренебрежение инерционными членами в уравнениях движения.

В следующем разделе перейдем к изучению специфических медленных волновых процессов: ионный звук и магнитная гидродинамика.