12.4. Релятивистская механика частицы. 4 – скорость. 4 – ускорение. Четырехмерное уравнение движения. 4 – импульс. Сила Минковского. Энергия частицы. Принцип эквивалентности.

1. В классической механике импульс частицы определяется как , где - масса частицы, - ее скорость. Такое определение не может быть правильным в теории относительности при требовании использования преобразования Лоренца. Дело в следующем: импульс может быть сколь угодно большим как в классической, так и в релятивистской механике, скорость же в теории относительности ограничена сверху величиной .Поэтому определение должно быть изменено.

Все физические величины могут быть объединены в совокупности, которые являются либо скалярами, либо 4 – векторами, либо ; 4- тензорами, либо спинорами (квадратичные комбинации спиноров образуют 4 - векторы). В математике доказано, что иных объектов, связанных с преобразованиями Лоренца не существует. Установив, вектором или тензором является некоторая величина, мы получаем возможность классифицирования всех физических величин. Так как все инерциальные системы отсчета эквивалентны, то все законы природы должны выглядеть одинаково в этих системах. Введя понятие 4 – вектора, либо 4 – тензора, следует каждому закону природы придать четырехмерную формулировку, она и будет инвариантной относительно преобразований Лоренца.

Релятивистская механика описывается в четырехмерном пространстве Минковского. При определении четырехмерных векторов (4 - векторов) скорости и ускорения за основу принимается 4 – вектор , записываемый в одной из двух форм (ковариантной или контравариантной):

, .

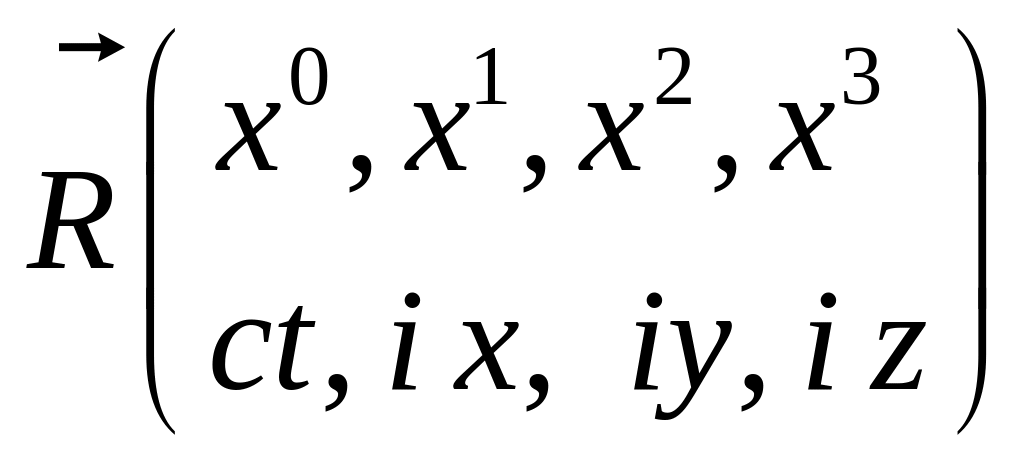4 – скорость можно определить отношением , где должен быть скаляром (все скаляры являются инвариантами для преобразования Лоренца). В качестве естественно взять некоторое «выделенное» время. Таким временем является собственное время частицы, определяемое однозначно через интервал

.

Скалярная функция является инвариантом. Напомним, что - скорость движения частицы и одновременно с этим, это скорость движения локально инерциальной системы . произвольная функция времени, и при введении понятия собственного времени использовалось требование, чтобы движущаяся система была бы «локально инерциальной» (инерциальной в течение бесконечно малого промежутка времени).

Таким образом, 4 – скорость определяется в виде

,

где - 4 – вектор, - скаляр (инвариант), значит, ковариантная 4 – скорость при переходе из одной инерциальной системы в другую должен преобразовываться согласно преобразованию Лоренца:

,

где , . При , - компоненты трехкомпонентной скорости. Четвертая компонента определяется соотношением

.

В контравариантной форме будем иметь

, ,

Таким образом, имеем две формы записи для 4 – вектора скорости частицы

, .

Квадрат 4 - скорости имеет вид

,

т.е. является инвариантом. 4 – вектор скорости касателен к траектории движения точки в 4 – мерном пространстве – времени и он сохраняет свою величину (модуль).

4 – ускорение определяется по формуле

.

Компоненты 4 – ускорения при определяются в виде

, , , .

В частном случае равномерного движения и . Квадрат 4 - ускорения удовлетворяет соотношению

.

Так как 4 – ускорение является производной от постоянного по величине (модулю) 4 – вектора скорости, то эти 4 – векторы ортогональны: ( )=0. Этот факт может быть получен так же из другого представления. Дифференцируя по собственному времени инвариантное соотношение

,

после дифференцирования по , получим

.

Это соотношение отражает отмеченный уже выше факт ортогональности 4 – скорости и 4 – ускорения: .

2. Получим четырехмерное уравнение движения частицы. В классической механике второй закон Ньютона (уравнение движения) записывается в форме трехмерного векторного уравнения

, (12.4)

где - трехмерный классический импульс частицы, - масса покоя частицы, - трехмерный вектор силы. В классической механике допустима ситуация . В релятивистской механике , но возможна ситуация .

Умножая (12.4) на , получим

.

Справа в этом соотношении стоит работа силы в единицу времени, значит, левая часть это изменение энергии. Энергию частицы можно записать в виде

,

где - кинетическая энергия частицы, - энергия покоя, потенциальная или внутренняя энергия частицы. В классической механике .

В релятивистской механике уравнение движения записывается в форме (12.4), но импульс и сила задаются в четырехмерном виде, а время заменяется собственным временем

, , (12.5)

4 – силу - в уравнении (12.5) еще нужно определить. 4 – импульс вводится по определению , где - масса покоя частицы, величина скалярная и поэтому инвариантная. Имеет место ортогональность векторов

.

.

Учитывая, что первые три компоненты уравнения движения (12.5) запишем в явном виде (12.6)

Если первые три компоненты 4 – силы определим как , где - обычная трехмерная сила, то с учетом такого определения (12.6) можно записать в векторной (трехмерной) форме аналогичной уравнению движения классической механики (12.4)

. (12.7)

На самом деле, это уравнение по внешнему виду не отличается от уравнения движения классической механики (12.4), если за трехмерный импульс принять величину . Отметим, что такой импульс в отличие от импульса классического связан со скоростью частица нелинейным соотношением, так как .

Рассмотрим теперь четвертую компоненту уравнения движения (12.5), в котором не ясным остается смысл компоненты силы . Оказывается, что она может быть найдена по известным первым трем компонентам 4 – силы. Используем отмеченный уже ранее факт ортогональности 4 – скорости и 4 – ускорения: :

. (12.8)

.

4 – сила называется силой Минковского . Выясним физический смысл четвертой компоненты уравнения (12.5):

,

или .

Справа здесь стоит работа силы в единицу времени, следовательно, слева в скобках должна стоять энергия (с точностью до постоянного слагаемого)

.

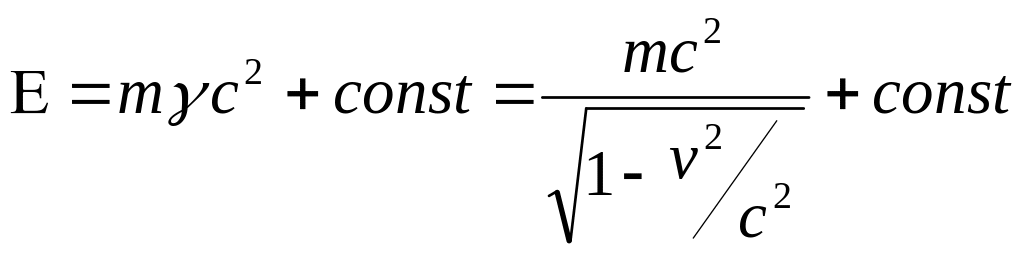В релятивистской механике делается выбор . Это позволяет импульс и энергию объединить в единый 4 – вектор импульса – энергии . При этом энергия покоящейся частицы представляется в виде скалярной величины (это инвариант)

.

Если покоящаяся частица теряет при излучении энергию , то ее масса покоя одновременно уменьшается на .

Переход из состояния покоя с энергией в состояние с энергией приводит к изменению массы на величину . При переходе от собственной системы отсчета (в ней частица покоится) к любой другой инерциальной системе энергия возрастает в раз. В релятивистской механике кинетическая энергия (энергия движения) получается вычитанием энергии покоя из полной энергии .

Еще раз напомним, что в классической механике .

3. Кроме инерциальных систем существует бесчисленное множество неинерциальных систем отсчета – систем движущихся с ускорением относительно инерциальных систем (такой системой является Земля, которая вращается вокруг своей оси, вокруг Солнца и вокруг центра нашей Галактики). Неинерциальными системами можно пользоваться при описании механических движений и любых физических процессов. Однако, инерциальные системы имеют преимущество простоты: свободное тело движется в них прямолинейно и равномерно. В неинерциальных системах возникают специфические силы: центробежная сила инерции, сила Кориолиса. Важнейшей особенностью сил инерции является то, что ускорение, вызываемое ими, не зависит от массы движущегося тела. По этой причине возникает аналогия между неинерциальными системами и гравитационными полями.

Пусть неинерциальная система движется прямолинейно с постоянным ускорением относительно инерциальной системы. В ней возникает сила инерции , где - масса тела. Если рассмотреть постоянное и однородное гравитационное поле с ускорением , то тело испытывает в нем действие силы . Если создать условие , то движение тела при наличии каких угодно добавочных сил, в неинерциальной системе происходит точно так же, как движение тела в инерциальной системе при наличии в ней гравитационного поля с ускорением . Неотличимость силы инерции, возникающей в неинерциальной системе, движущейся прямолинейно и равномерно ускоренно, от однородного гравитационного поля называют принципом эквивалентности. Неинерциальные системы эквивалентны инерциальным системам с введением в них некоторых гравитационных полей. В гравитационном поле пространство перестает быть евклидовым. При этом геометрические свойства перестают быть абсолютными, они зависят от гравитационных полей. Гравитационные поля создаются материей. Поэтому геометрия пространства определяется материей. Геометрия пространства теряет свое самостоятельное существование и становится частью физики. Это же относится и ко времени. В этом состоит основная идея общей теории относительности Эйнштейна (1915 г.).

12.5. Движение заряженной частицы во внешнем постоянном электромагнитном поле в вакууме. Циклотронная частота.

Сначала исследуем следующую ситуацию.

1). На частицу с зарядом действует трехмерная сила

,

где - скорость частицы. Получим описание релятивистского ускорения частицы .

Первые три компоненты уравнения движения - трехмерное уравнение движения имеет вид

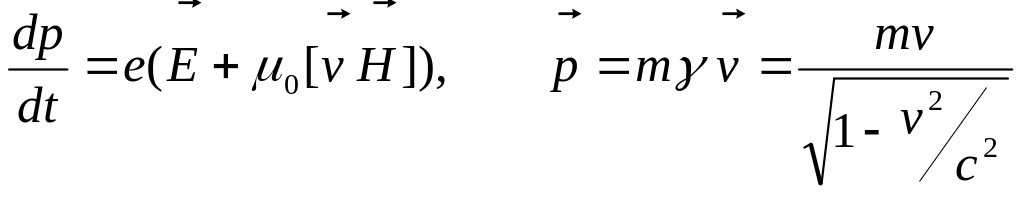. (12.8.А)

Следует отметить, что это нелинейное уравнение. Изменение энергии частицы во времени описывается соотношением (это четвертое уравнение движения)

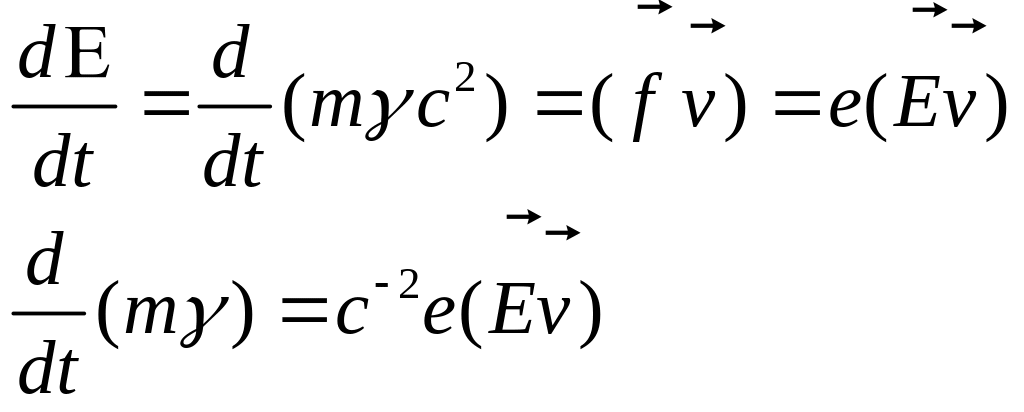, (12.9)

изменение энергии частицы определяется только электрическим полем, так как магнитная сила перпендикулярна скорости, и она не производит работы.

Подстановка этого выражения в уравнение движения (12.8.А) позволяет найти релятивистское ускорение частицы как нелинейную функцию скорости частицы

.

Учет релятивистских эффектов в формуле для ускорения дает два отличия от описания классической механики: во – первых появляется характерный множитель , а во – вторых, возникает добавочный член с напряженностью электрического поля .

2). Рассмотрим частный случай . Найдем закономерность эволюции и определим траекторию частицы. Введем систему координат следующим образом: , , где . Тогда из уравнения движения

Получим ,

значит, имеет место описание эволюции компонент вектора

.

Из представления получим описание скорости , и описание траектории частицы.

Для выполнения этой задачи понадобится представление комбинации .

Начало отсчета времени выберем так, чтобы .

.

Полученные соотношения представляют собой нелинейные уравнения относительно вектора скорости.

Примем во внимание соотношения

и получим представление

Учитывая соотношение , получим описание эволюции вектора скорости как функции времени. Компоненты вектора скорости заряженной частицы, находящейся во внешнем электрическом поле имеют вид

, .

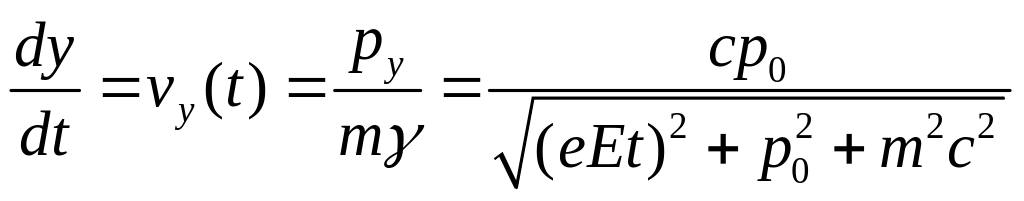При неограниченном возрастании времени проекция скорости вдоль поля стремится к скорости света , а перпендикулярная проекция скорости стремится к нулю. Учитывая, что и , можно определить траекторию частицы. Можно показать, что она имеет вид параболы

.

3). Исследуем теперь движение частицы в постоянном магнитном поле при отсутствии электрического поля. Последнее обстоятельство (см. пункт 1).) приводит к сохранению энергии

, .

Вектор вращается, не изменяя величины

Трехмерное уравнение движения линейно, и имеет вид

.

Получаем формулу для ускорения ,

где угловая скОрость называется циклотронной частотой (частотой гирорезонанса заряженной частицы). В нерелятивистской ситуации . Вектор скорости представим в виде суммы , где - компонента вдоль направления вектора Индексом отмечена компонента вектора, перпендикулярная . Движение в плоскости , перпендикулярной вектору происходит по окружности:

., , .

Радиус этой окружности дается формулой ,

так как .

Составляющая вектора скорости частицы вдоль не изменяется, поэтому траектория частицы это винтовая линия с осью, направленной вдоль , и с радиусом .

12.6. Эффект Доплера. Аберрация света. Преобразование Лоренца может быть использовано для описания релятивистского эффекта Доплера и эффекта аберрации света (аберрация света анализировалась в разделе 12.3). Рассмотрим 4- вектор . Плоская монохроматическая волна имеет вид (по – сути, обсуждаются свойства Фурье - образа). Здесь частота и волновое число связаны между собой дисперсионным соотношением. Ограничившись распространением волны в вакууме, будем иметь представление . При преобразовании Лоренца поле и его Фурье - образ преобразуются одинаково. Фаза стоит в показателе экспоненты, значит, она скаляр и она должна быть инвариантом. Введем в рассмотрение два 4 – вектора с компонентами и . То, что компоненты являются компонентами 4 – вектора (его называют волновым 4 - вектором), следует из представления , где - скаляр, - компоненты 4 – вектора. Значит, волновой 4 – вектор преобразуется согласно преобразованию Лоренца. 3 – вектор преобразуется как 3 – вектор , преобразуется как . Таким образом, преобразуется как время . Имеет место соответствие

Пусть инерциальная система движется с постоянной скоростью относительно инерциальной системы и пусть в системе волновой вектор и частота равны и .

Преобразование Лоренца, соответствующие трехмерному движению системы относительно системы получено в разделе 12.1, и оно имеет вид

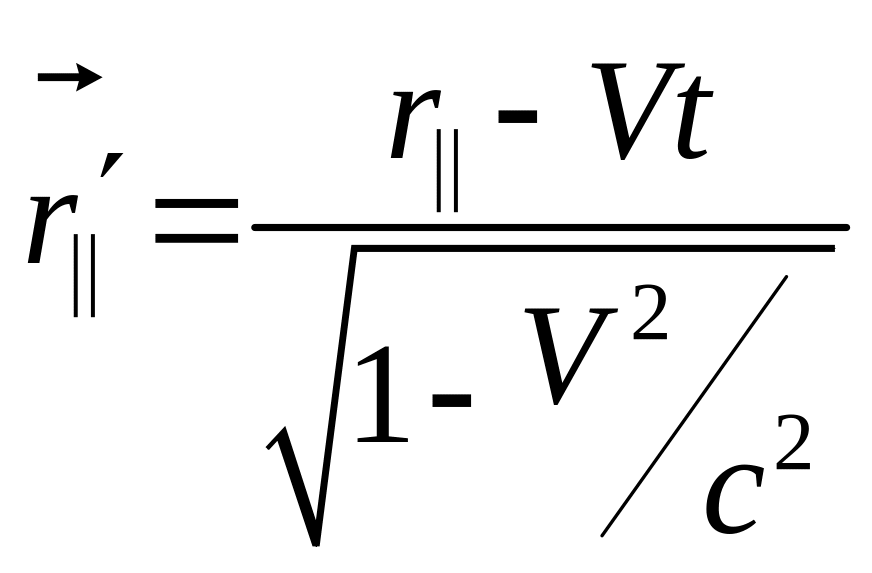(12.10) . (12.11)

Переход к нашей задаче соответствует формальной замене . Из формул (12.10), (12.11) имеем

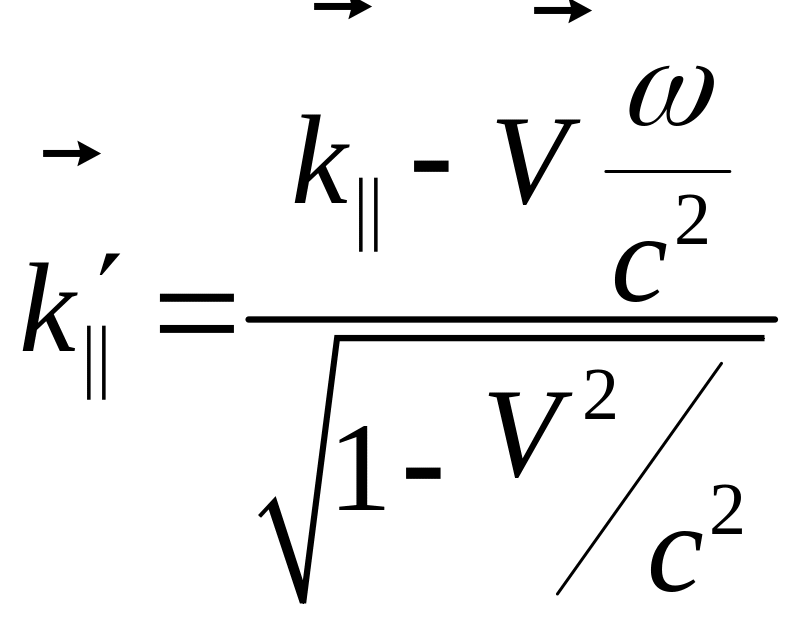, (12.10.А) 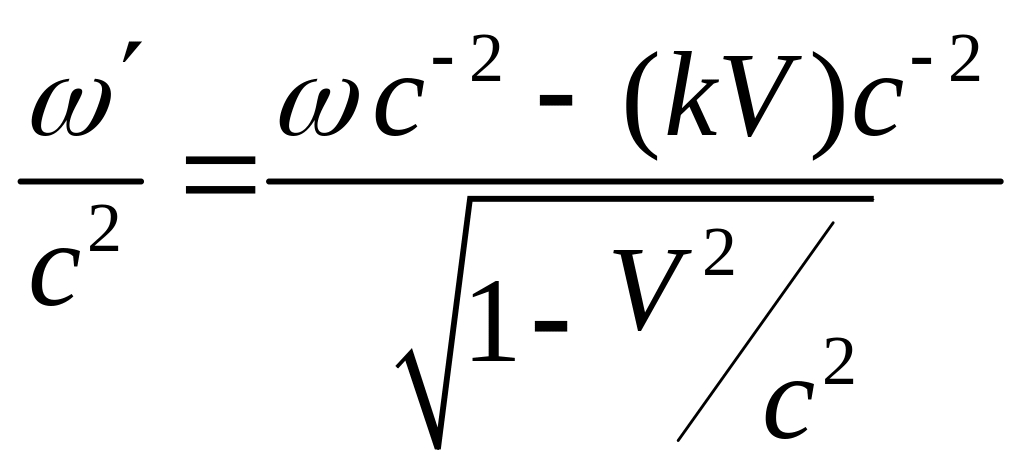(12.11.А)

где ,

- угол между векторами и .

Из (12.11.А) имеем описание эффекта Доплера .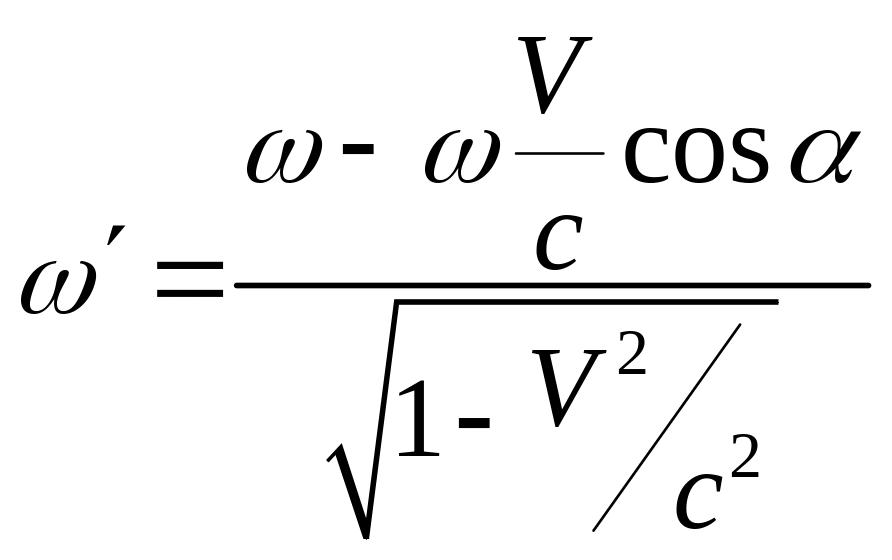

Учитывая эту связь, из (12.10.А) получим правило преобразования волновых векторов и описание аберрации света . (12.12)

Формула (12.12)описывает изменение направления распространения света в вакууме при переходе из одной инерциальной системы в другую (эффект аберрации света), а формула (12.11.А) определяет соответствующее изменение частоты – релятивистский эффект Доплера.

12.7. Преобразования Лоренца 4-х мерного потенциала и 4-х мерного тока в электродинамике.

Уравнения электродинамики, в отличие от уравнений классической механики, инвариантны относительно преобразования Лоренца. Для удобства преобразования полей при переходе из одной инерциальной системы в другую, целесообразно ввести понятия 4 – векторов и 4 – скаляров в четырехмерном пространстве – времени.

В вакууме система уравнений Максвелла имеет вид

, (12.13) , (12.14)

, (12.15) , (12.16) .

Введя трехмерный векторный и скалярный потенциалы

.

При выполнении калибровки Лоренца

,

уравнения (12.13) – (12.16) можно свести к уравнениям для потенциалов

, , (12.17)

где символ означает оператор Д’Аламбера

,

Трехмерные уравнения (12.17) можно записать как одно четырехмерное уравнение для 4 – потенциала и 4 – вектора плотности стороннего тока :

. (12.18)

Условие калибровки и закон сохранения зарядов в источнике можно записать в 4 – мерной форме, используя определение дивергенции

. (12.19)

. (12.20)

Уравнения (12.18) – (12.20) справедливы в любой инерциальной системе отсчета. Инвариантность этих уравнений обеспечивается благодаря инвариантности трехмерных уравнений Максвелла относительно преобразования Лоренца.

Преобразование Лоренца для произвольного 4 – вектора можно записать в матричной форме. В случае движения системы вдоль оси относительно системы это преобразование имеет вид

где - компоненты 4 - тензора второго ранга: ,

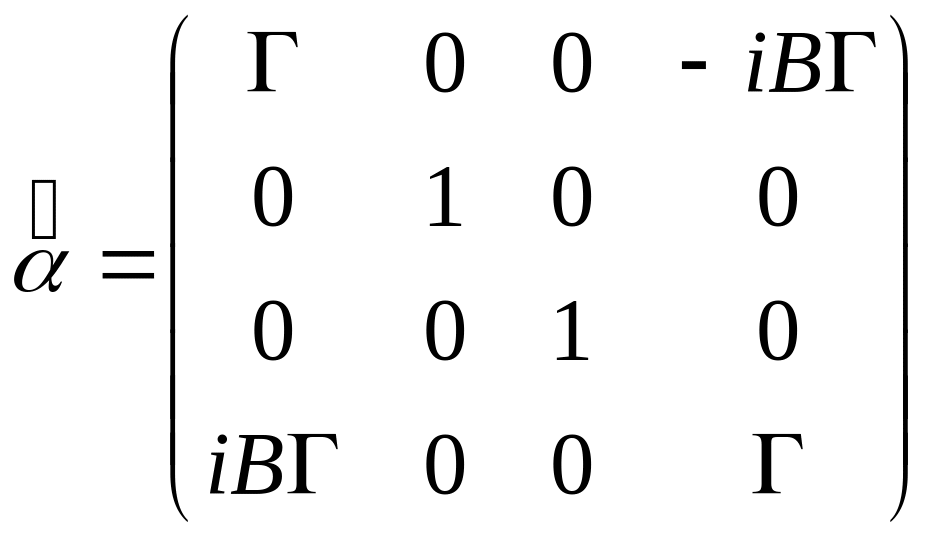где .

Компоненты получаются из заменой строк на столбцы (для тензора это делается заменой на ).

В частности для 4-вектора , в случае движения системы вдоль оси относительно системы , преобразование Лоренца имеет вид

(12.21)

Преобразование (12.21) удовлетворяет матричной форме

,

Преобразования 4 – потенциала и 4 - тока имеют вид

.

Пример №1. Если в системе отсчета заряд покоится, то тока в этой системе нет, . В системе будем иметь

.

Из первого и из последнего соотношений получаем формулы преобразования плотности тока и плотности заряда

.

С учетом последнего равенства, можно получить .

Изменение плотности заряда при переходе от к обусловлено изменением объема . Действительно, заряд в обеих системах одинаков, а плотность заряда определяется соотношениями

.

Таким образом, полный заряд в заданном объеме остается неизменным

.

Пример №2. Вторым частным случаем является ситуация, когда в системе имеется незаряженный проводник, по которому течет ток

,

тогда в системе будет некоторая плотность заряда .

.

Эта плотность заряда в системах и определяется формулой

, .

12.8. Тензор электромагнитного поля в вакууме. Трехмерное поле и связано с потенциалами

.

Учитывая определение 4 – потенциала , получим компоненты полей

, ,

, ,

,

.

Компоненты вектора определяются по закону

Таким образом, компоненты векторов выражаются через компоненты 4-х потенциала в виде комбинаций . Введем в рассмотрение антисимметричный 4 – тензор второго ранга (его называют тензором электромагнитного поля) , (12.22)

Учитывая приведенные выше соотношения, получим представление этого тензора в виде

.

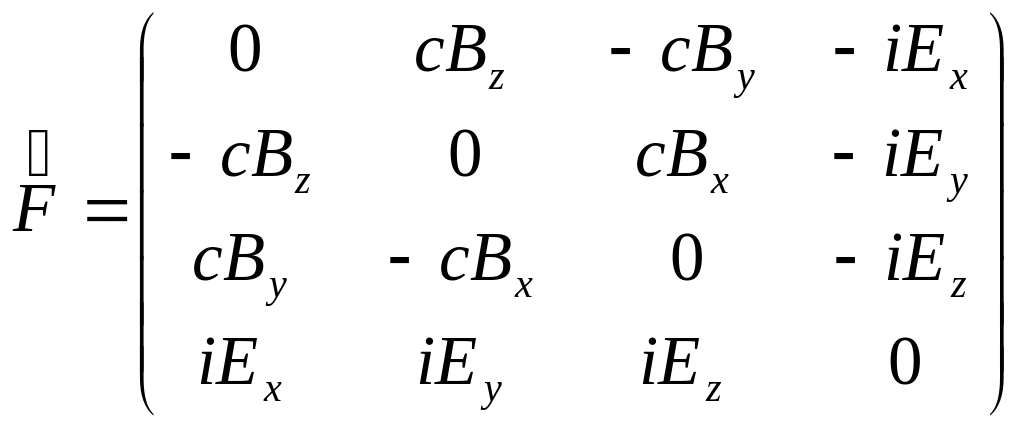В четырехмерном пространстве Минковского поля и выступают не независимо, а как составляющие единого четырехмерного электромагнитного поля, описываемые тензором . Компоненты 4 – тензора преобразуются при лоренцовском преобразовании по формуле

, (12.22.А)

Электрическое и магнитное поля неразрывно связаны между собой. Поле от одного источника в разных инерциальных системах имеет разный вид. Если в одной инерциальной системе было только электрическое поле, то в другой инерциальной системе отсчета появится еще и магнитное поле.

12.9. Тензор индукции. Для описания поля в веществе, кроме полей и необходимо ввести еще два вектора, например вектор электрической индукции и вектор магнитного поля , или вектор электрической поляризации и вектор намагничивания . Имеются две связи между этими векторами

.

Векторы и образуют тензор индукции получаемый из тензора заменой компонент на , а компонент на :

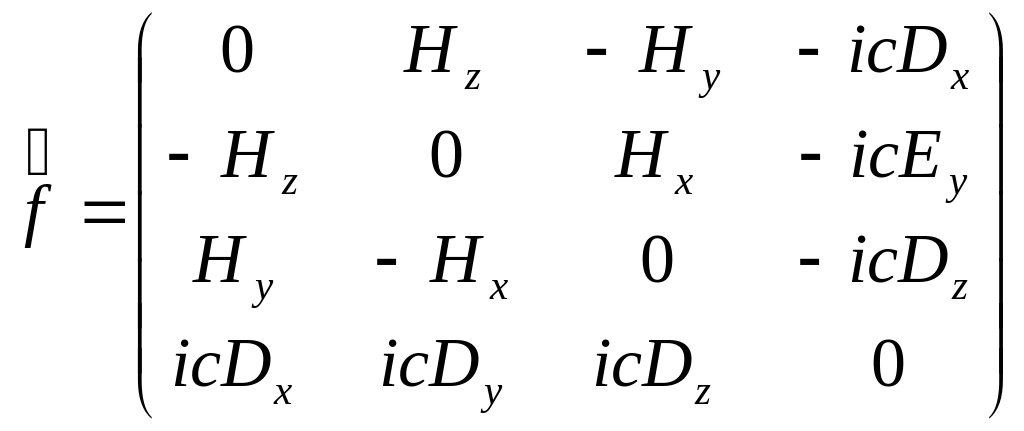. (12.23)

На основе тензоров и решается задача о преобразовании компонент поля при переходе из одной инерциальной системы в другую. где - матрица преобразования Лоренца. Преобразование (12.23) получается как преобразование произведения двух 4 – векторов и

, .

В качестве примера применим (12.22.А) для вывода преобразования компоненты поля . Формула преобразования имеет вид

.

Учитывая, что , получим . Поэтому

,

где . Приходим к формуле преобразования

.

Аналогично получаются формулы преобразования для других компонент поля. Формулы преобразования удобно записывать в векторной форме, для этого поля разобьем на составляющие, параллельные и перпендикулярные направлению движения системы

, , , .

Учитывая, что , получаются формулы

, ,

, .

Формулы обратного преобразования получаются заменой величин со штрихом на соответствующую величину без штриха и наоборот, а так же изменением знака у .

Рассмотрим две предельные ситуации.

1.). В системе отсутствует магнитное поле . В системе будет и электрическое поле и магнитное:

,

.

Последнее Равенство показывает, что поля и ортогональны. Следует отметить, что эту ортогональность можно обнаружить не делая преобразований. В самом деле, скалярное произведение является инвариантом, а в рассматриваемом примере и значит , т.е. и - ортогональны.

2.). В системе отсутствует электрическое поле . В системе будет и электрическое поле и магнитное, можно сразу отметить, что :они будут ортогональны

.

С учетом последнего соотношения можно переписать выражение для поля в виде

, где учтено, что

12.10. Релятивистская 4 – сила Лоренца. Плотность трехмерной силы Лоренца (сила, действующая на заряды в единичном объеме среды) определяется формулой

,

где - скорость заряженной среды и плотность зарядов.

Обобщение на четырехмерный случай делается следующим образом. Ранее введены понятия: 4 – вектор тока и тензора электромагнитного поля

Введем в рассмотрение 4 – вектор

.

Выпишем компоненты этого 4 – вектора (он называется плотностью силы Лоренца)

,

где учтено соотношение .

Аналогично находятся остальные три компоненты

, , .

Четвертая компонента силы находится следующим образом:

Первые три компоненты совпадают с соответствующими компонентами трехмерной плотности силы Лоренца. Сделаем преобразование:

,

поэтому можно плотность силы Минковского представить в виде

.

В частном случае сопутствующей системы отсчета заряды неподвижны и в системе будем иметь :

.

При .

Введенная 4 – плотность силы Лоренца позволяет написать четырехмерное релятивистское уравнение движения заряженной среды в виде ,

где - собственное время, - 4 – импульс.

12.11. Тензорная форма уравнений Максвелла. Уравнения Максвелла в трехмерной формулировке возьмем в виде

, (12.24) (12.25)

Для записи уравнений (12.24) в тензорной форме, вместо тензора электромагнитного поля удобнее использовать дуальный тензор , который отличается от заменой компонент на и замены на

.

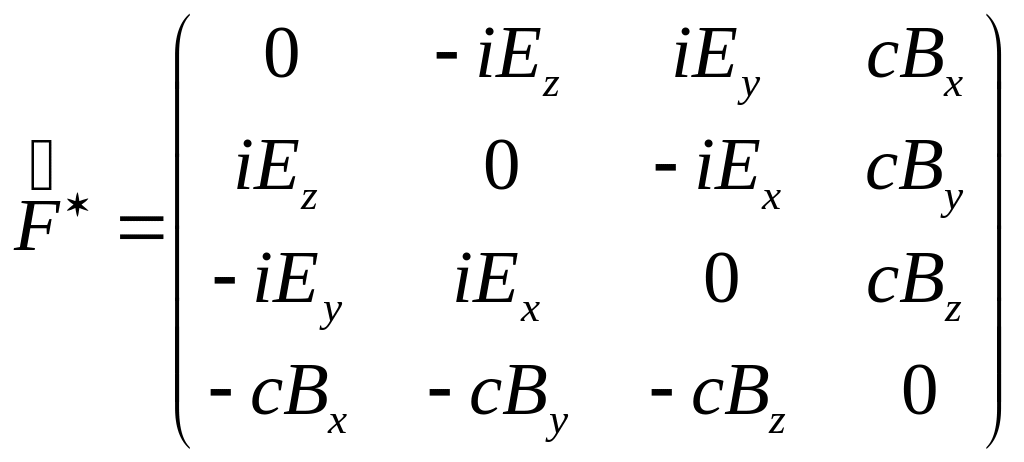В результате система (12.24) приводится к тензорной форме .

Принимая во внимание вид тензора индукции (12.23) , система (12.25) приводится к тензорной форме .