11.3. Описание лучевой картины для типичных случаев неоднородности.

1). Рассмотрим задачу о картине лучей в неоднородной безграничной среде, квадрат показателя преломления которой изменяется с высотой по линейному закону

.

Уравнение луча в такой среде принимает вид

.

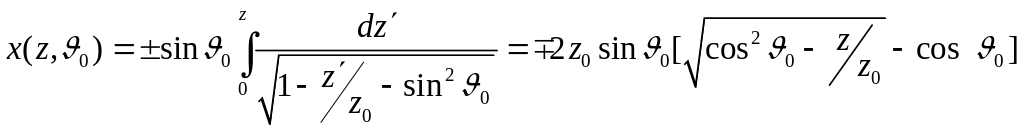Таким образом, лучи являются параболами. Для луча, идущего в сторону увеличения координат и , следует брать верхний знак Высота точки поворота находится из условия и выражается формулой

.

Уравнение луча приводится к виду

.

Горизонтальная координата точки поворота дается формулой

.

Найдем горизонтальную координату («дальность») луча, пришедшего на тот же уровень, с которого он и вышел ( ) (Рис.11.5)

.

Одной дальности соответствует два луча, вышедшие из источника под углами и (Рис. 11.6). Таким образом, в одну точу , на уровне приходят два луча при условии , а при сюда не приходят лучи. Это соответствует отмеченной выше ситуации, когда задача нахождения угла выхода при фиксированных положениях источника и точки наблюдения, имеет не единственное решение.

Найдем геометрическое место точек поворота. Оно определяется системой уравнений

,

из которой получаем

.

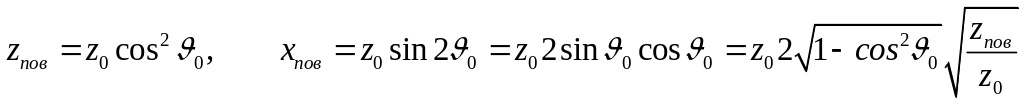Соответствующая кривая изображена сплошной линией на Рис.11.7 в плоскости . Геометрическое место точек поворота в этой плоскости является эллипсом

.

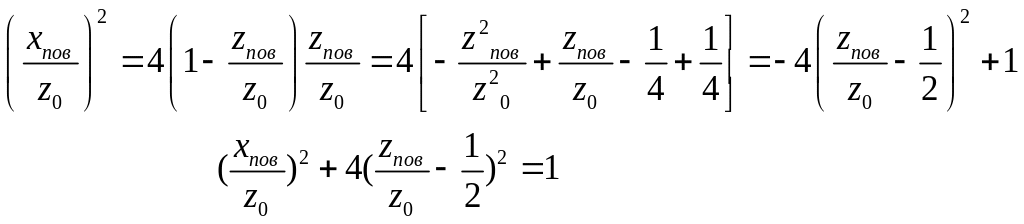Определим положение каустики в плоскости из системы уравнений

,

которая приводится к виду

.

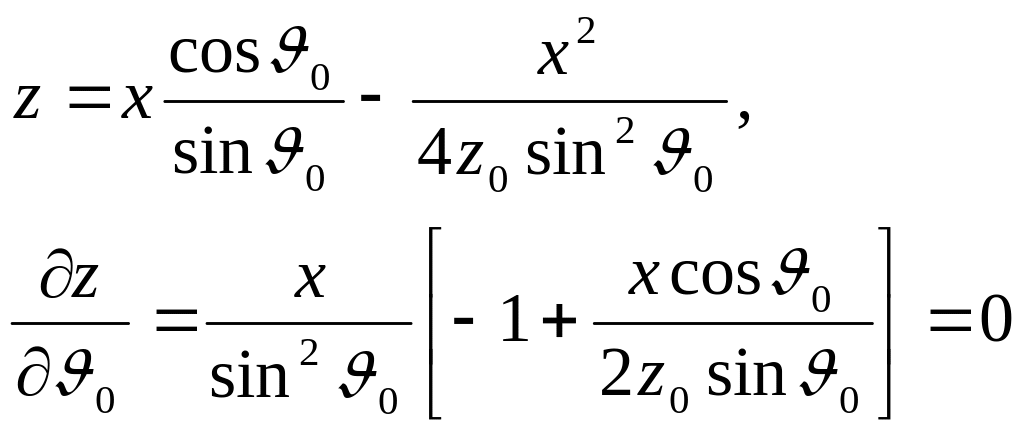Исключая угол из этой системы, получим уравнение каустики

.

Линия каустики в плоскости является параболой с вершиной при . Она изображена штриховой линией на Рис.11.7, 11.8 и 11.9. На Рис.11.8 показана качественная картина семейства лучей для линейного профиля неоднородности среды. Каустика в этом случае разделяет пространство на область «тени» (в ней нет лучей) и «освещенную» область, в которой в каждую точку приходят от источника два луча. На Рис.11.9 сплошными линиями показано семейство поверхностей равной фазы. «Яйцеобразный» вид фазовых поверхностей в начальные моменты времени, (пока лучи еще не достигли каустики), связан с тем, что фазовая скорость волны в направлении возрастания оказывается больше, чем в противоположном направлении.

2). В случае полу бесконечного линейного слоя в области , граничащего с однородным полу пространством (Рис.11.10). Функция имеет вид

.

Форма каустики усложняется. Вместо гладкой формы, теперь возможно появление каустик с особенностями в виде «петли» с двумя точками заострения («ласточкин хвост»). Форма каустики при этом зависит от положения точечного источника ( ). В области среда однородная и лучи здесь представляют собой прямые линии. В области профиль неоднородности линейный и лучи здесь имеют вид отрезков парабол. Не приводя формул для описания геометрического места точек поворота и каустики, отметим основные закономерности лучевой картины. Оказывается, что каустика имеет гладкую форму, если источник расположен либо ниже уровня , либо выше уровня . При условии на каустике имеются точки заострения, ограничивающие каустическую петлю. Эволюция формы каустики при изменении высоты положения источника показана на Рис.11.11. При и петля на каустике стягивается в каустические фокусы и . Через каждую точку внутри каустической петли проходит четыре различных луча. (три луча, претерпевших поворот и один луч - прямой). Поясним появление петлеобразной каустики. Рассмотрим форму линии, изображающей геометрическое место точек поворота лучей. При условии или (такая ситуация на Рис.11.12 и 11.14 отмечена буквой ) линия геометрического места точек поворота в плоскости является монотонной (Рис.11.12). Монотонной при этом оказывается и линия каустики, которая разделяет в этом случае пространство на область тени и на освещенную область (в каждую точку здесь приходят два луча). В этом случае однозначной будет зависимость дальности от угла выхода (случай на Рис.11.13). Ситуация изменяется при (случай ). Как видно из Рис.11.13, некоторым дальностям соответствуют три значения угла выхода . В соответствующую область пространства (в каустическую петлю приходят три луча, претерпевших поворот). В случае геометрическое место точек поворота лучей уже не является монотонной кривой (Рис.11.14) и функция имеет две точки экстремумов. Отсутствие монотонности этой кривой определяет особый характер каустики в случае .

Еще более сложный вид каустик может возникать при рассмотрении лучевой картины для сред с другой зависимостью показателя преломления от координаты . Естественно, что картина лучей и конфигурация каустики еще более усложнится в случае, когда показатель преломления зависит от всех трех координат . Дополнительное усложнение картины происходит в неоднородных анизотропных средах.

11.4. Оптико–механическая аналогия: взаимосвязь между принципами Ферма и Мопертюи. Постоянная Планка, длина волны де Бройля. Уравнение Шреденгера. Соотношение неопределенностей Гейзенберга. Радиус Бора Луч в геометрической оптике подобен траектории материальной частицы в механике. Существует аналогия между принципом Ферма в геометрической оптике и принципом Мопертюи в механике. Принцип Ферма утверждает минимальность оптического пути высокочастотного электромагнитного поля (света). Интеграл, взятый вдоль луча между двумя точками минимален по сравнению с оптическим путем, вычисленным вдоль любой другой кривой, соединяющей те же точки и 2:

,

где - волновой вектор, - частота волны, , волновой вектор направлен по касательной к лучу.

Принцип Мопертюи утверждает минимальность интеграла действия

,

взятого вдоль истинной траектории частицы, по сравнению с таким же интегралом, взятом вдоль любой другой кривой, соединяющей те же две точки, - импульс частицы.

Уравнение движения частицы в потенциальном поле в нерелятивистском случае имеет вид

Здесь - масса частицы, - потенциальная энергия.

Так как (здесь штрихом обозначена производная по времени), то из уравнения движения следует закон сохранения энергии

, или .

, .

- импульс частицы, он направлен по касательной к траектории частицы, - энергия частицы - скорость частицы.

.

Имеет место аналогия . Аналогом материальной точки в механике является волновой пакет в геометрической оптике. Должна иметься аналогия ( - скорость частицы), . Отсюда следует аналогия . Количественная формулировка оптико-механической аналогии выглядит следующим образом

,

где - постоянная Планка. В частности имеем или - длина волны де Бройля. Фазовая скорость имеет представление . Волновому уравнению в электродинамике сопоставим аналогичное волновое уравнение для механики

,

где - волновая функция, описывающая монохроматическую волну , для которой волновое уравнение приводится к виду уравнения с переменным коэффициентом : .

Это уравнение Шреденгера для комплексной амплитуды волновой функции в квантовой механике. Величина описывает распределение вероятностей нахождения частицы в том или ином месте пространства. Возникает вопрос, почему имеет место квантование? Это обусловлено тем, что при заданной потенциальной энергии уравнение Шредингера допускает решение не при всех, а только при определенных значениях энергии . Этот набор энергий называется спектром энергий. Спектр может быть дискретным (наличие квантования) и может быть сплошным. Если в качестве примера взять (это соответствует потенциальной энергии электрона в поле протона), то можно получить энергетический спектр атома водорода.

Для волнового пакета (квазимонохромата) имели место соотношения

.

Аналогами их в квантовой механике будут соотношения неопределенности Гейзенберга

.

Если частица локализована в интервале по оси , то проекция ее импульса на эту ось не может иметь определенного значения, а лежит в интервале при выполнении условия (аналогично для осей и ). Если частица нестационарна в течение времени , то это состояние не может быть моноэнергетическим. Мера немоноэнергетичности связана с соотношением Гейзенберга.

Оценку величины радиуса самого легкого атома – атома водорода можно получить на основе предельной ситуации, заменяя неравенство Гейзенберга равенством , сделав дополнительно четыре допущения:

(1) - минимальный размер атома (радиус Бора)

(2) , здесь - масса и

кинетическая энергия электрона

(3) - потенциальная энергия электрона (4) .

Из этих соотношений получается представление радиуса Бора

.

Возможно обобщение классической квантовой механии на случай релятивистской квантовой механики при введении биспинора (четыре волновых функции), который удовлетворяет уравнению Дирака. Система уравнений Дирака совместно с уравнениями Максвелла описывают квантовую электродинамику. В этом описании возникают эффекты: 1). Электрон обладает внутренним моментом количества движения – спином (он равен в единицах квантовой постоянной). 2). Электроны могут иметь состояния с отрицательной энергией (бесконечный фон электронов составляет электронный вакуум). Такое состояние соответствует наличию позитронов – это античастицы по отношению к электронам. Позитроны имеют массу электрона и их заряд отличается от заряда электрона только знаком. Электромагнитное поле и электроны с позитронами выступают в квантовой электродинамике как две равноценные формы единой материи.

11.5. Принцип Гюйгенса и дифракция Френеля. Геометрическая оптика соответствует коротковолновому приближению для электромагнитных волновых процессов (длина волны ). При конечных значениях длины волны возникают отличия от геометрической оптики, – они носят общее название дифракции. Имеет место соотношение неопределенностей

,

где -характерный разброс волнового числа, - характерный разброс неоднородности среды (размер экрана на Рис.11.15, Рис.11.19). В соответствии с Рис.11.19 имеем при , .

Из соотношения неопределенностей получается представление

.

На расстоянии от экрана поперечный масштаб увеличивается на величину . Выделяются три ситуации

- геометрическая оптика,

- дифракция Френеля,

- дифракция Фраунгофера.

Параметр называется волновым параметром, а параметр называется числом Френеля.

1). Дифракционные явления можно приближенно исследовать на основе использования принципа Гюйгенса (речь будет идти о поправках к геометрической оптике). Рассмотрим следующую задачу. На пути распространения электромагнитного поля от источника к точке наблюдения находится непрозрачный экран с отверстием (Рис.11.15). Считается, что волна распространяется в вакууме. Принцип Гюйгенса предлагает считать отверстие закрытым произвольной поверхностью , которая является источником вторичных волн, распространяющихся за экран (в частности в точку ). При этом считается, что источник сам непосредственно не создает поле в точке . Источник создает только вторичные источники на поверхности . Этими вторичными источниками являются элементы поверхности . Монохроматическое поле, создаваемое на элементе равно , где - расстояние от источника до элемента . Это поле пропорционально , где - угол между нормалью к элементу и направлением луча, падающего на площадку . Это поле создается источником на элементе в том случае, если бы никакого экрана не было. Элемент создает за экраном сферическую волну, амплитуда которой убывает по закону , где - расстояние от элемента до точки наблюдения . При распространении сферической волны нужно учесть эффект запаздывания ее. Для этого при нахождении поля в точке в момент времени , нужно взять поле на элементе в боле ранний момент времени Поле, создаваемое в точке , представляется в виде

, где .

Математическая формулировка принципа Гюйгенса заключается в следующем: результирующе поле находится в виде суперпозиции

,

Доказательство применимости принципа Гюйгенса основано на сравнении с результатами точно решаемых задач, имеется также обоснование на основе асимптотических методов.

Ниже рассмотрим два простейших дифракционных явления: дифракция Френеля (расстояние между и конечно) и дифракция Фраунгофера ( и находятся на бесконечности).

2). При рассмотрении дифракции Френеля будем интересоваться поправками к геометро-оптическому приближению. Поэтому учтем вклад только участков поверхности , примыкающим к ломаной прямой, которая соединяет и . Считаем, что в окрестности рассматриваемой области, этот край расположен вдоль оси . Пусть источник и приемник расположены в плоскости . Соответствующий участок края экрана будем считать прямолинейным. Амплитуда поля изменяется медленно по сравнению с изменением фазы, поэтому

Будем считать, что экран совпадает с нижней полуплоскостью (Рис.11.16), так что ось направлена по краю экрана. Ось ортогональна поверхности экрана и на этой

оси на расстоянии находится источник (слева от начала координат). Координаты точки наблюдения равны , координаты источника равны . Тогда координаты элемента равны и , . Наиболее существенны только близкие к точке участки , поэтому возможны упрощения на основе малости величин по сравнению с

.

Учитывая, что , получим

. .

Верхний предел интегрирования взят равным , так как область больших не дает существенного вклада в результат интегрирования. Воспользуемся представлением

,

,

где .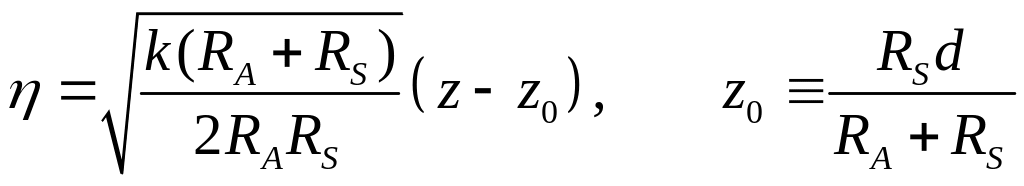

Результат преобразования имеет вид

.(11.8)

Последний интеграл называется интегралом Френеля. Так как , то .

В случае точка наблюдения лежит в области тени, интегрирование в (11.8) происходит в области выполнения неравенства . Имеет место приближенная формула

.

При точка наблюдения лежит в освещенной области, интегрирование в (11.8) частично происходит в области, где нарушается неравенство (это область в окрестности ). Сделаем следующее преобразование

Квадрат модуля интеграла Френеля определяет интенсивность электромагнитной волны. График зависимости ( интенсивность вдали от экрана) изображен на Рис.11.17. Вблизи экрана интенсивность в четыре раза меньше . Если двигаться в освещенную область, то интенсивность увеличивается и становится в максимуме порядка , далее начинаются осцилляции и приближение интенсивности к значению .

11.16. Дифракция Фраунгофера. Найдем теперь поле дифрагировашей электромагнитной волны в случае, когда источник и точка наблюдения удалены на бесконечность (Рис.11.18). Будем по-прежнему использовать принцип Гюйгенса, взяв за поверхность плоскость, закрывающую отверстие. Точка находящаяся на будет началом координат, радиус вектор направлен из точки в элемент . Падающее поле в точке поверхности представим в виде . Точка наблюдения находится далеко от отверстия экрана, поэтому направление дифрагирующего луча совпадает с направлением радиус-вектора этой точки. Волновой вектор дифрагировавшего поля направлен вдоль вектора . - радиус вектор, направленный из элемента в точку наблюдения, причем и .

Следовательно, . На основе принципа Гюйгенса имеем поле в точке наблюдения

,

- угол падения луча на площадку , .

В отличие от дифракции Френеля, в которой был существенен вклад лишь небольшого участка поверхности , при дифракции Фраунгофера существенна вся эта поверхность.

В качестве примера рассмотрим дифракцию на бесконечно длинной щели с параллельными границами в непрозрачном экране (Рис.11.19). Пусть волновой вектор падающей волны ортогонален к плоскости экрана . Угол дифракции - это угол между векторами и . Ширина щели , поэтому имеем

,

где учтено, что , . Интенсивность дифрагировавшей в интервал углов волны пропорциональна :

.

Найдем коэффициент пропорциональности, используя представление для суммарной интенсивности волны, падающей на щель

.

Зависимость интенсивности дифрагировавшего луча от угла дифракции показана на Рис.11.20, где введено обозначение . Интенсивность имеет ряд быстро убывающих максимумов, разделенных минимумами при , в которых она обращается в нуль. Установив положение минимумов (или максимумов) можно определит длину волны. Точность такого определения длины волны по дифракции на одной щели невелика из-за слабой резкости. Точность можно повысить, используя дифракционную решетку (совокупность одинаковых параллельных щелей, расположенных на равном расстоянии друг от друга).

12. Специальная теория относительности.

12.1. Преобразования Лоренца. Промежуток времени между событиями. Длина отрезка. Лоренцово сокращение. Четырехмерное пространство Минковского.

Экспериментальным фактом является то, что в вакууме распространяются электромагнитные волны с определенной скоростью . Эта скорость не зависит от выбора инерциальной системы отсчета. На первый взгляд это кажется неверным, так как противоречит закону сложения скоростей классической механики. Согласно этому закону, если скорость волны в инерциальной системе отсчета , то в другой инерциальной системе отсчета скорость волны должна быть , где - скорость системы относительно системы Дело в том, что необходимо отказаться от абсолютного характера времени и от преобразования Галилея для координат в системах отсчета и :

, ,

где - время, одинаковое в обеих системах отсчета.

Покажем, что в электродинамике справедливо другое преобразование (оно называется преобразованием Лоренца) для координат и времен событий в инерциальных системах отсчета и . Рассмотрим процесс распространения плоских волн в вакууме, описывая его волновым уравнением в инерциальной системе для скалярной функции

,

тогда соответствующее волновое уравнение для скалярной функции в инерциальной системе отсчета должно иметь вид

,

где учтено, что . Так как обе системы отсчета инерциальные, то имеет место неизменность (инвариантность) скалярных функций . Такая связь невозможна, если справедливо преобразование Галилея. Волновые уравнения – линейные, поэтому должно существовать линейное преобразование координаты и времени события в виде

,

где - некоторые константы, зависящие от параметров, описывающих задачу (определяющих параметров) ( - скорость движения систем отсчета относительно друг друга). Первая производная по координате представляется в виде

,

где учтено, что и вторые производные связаны соотношениями

,

.

Неизменность (инвариантность) волнового уравнения при переходе в другую инерциальную систему отсчета приводит к трем условиям

.

Имеет место преобразование координаты . Для того, чтобы это новое преобразование переходило в преобразование Галилея при , необходимо взять . Следствием последнего является представление 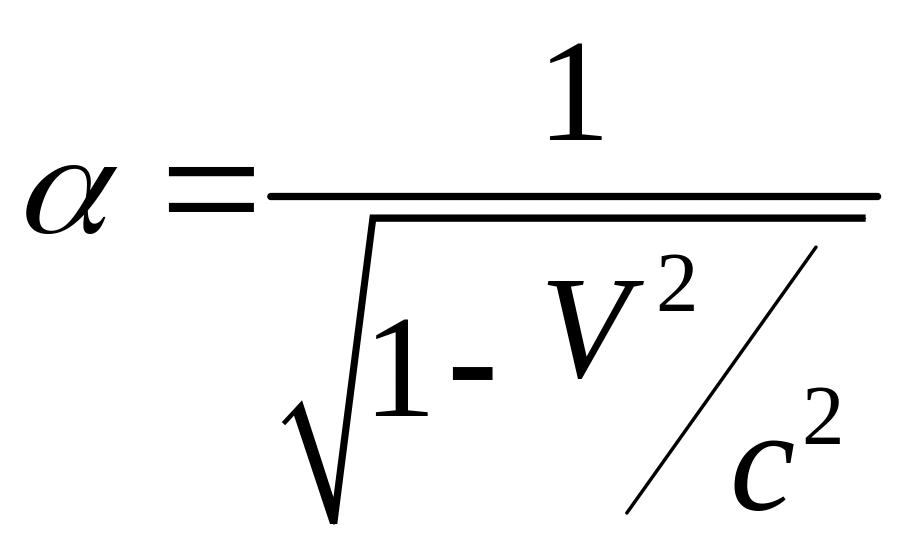. В результате получим преобразование Лоренца 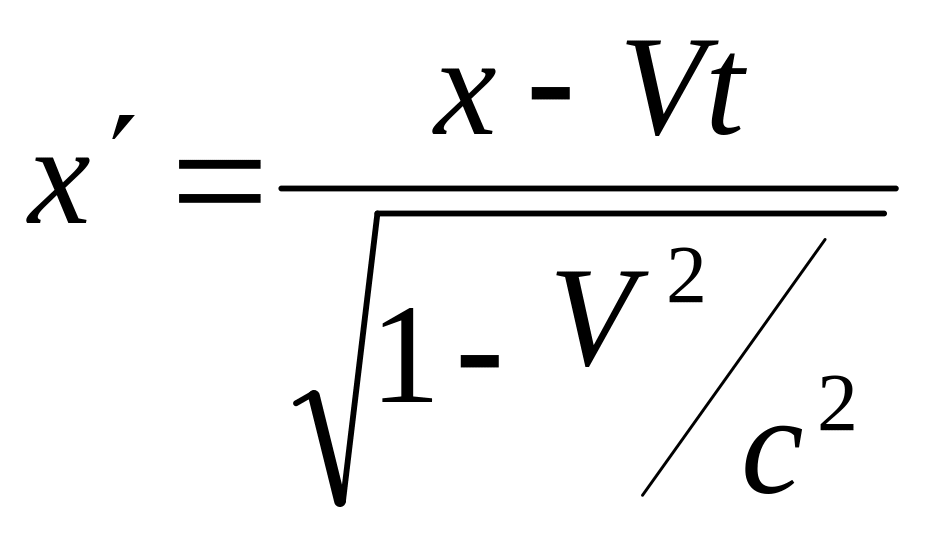, 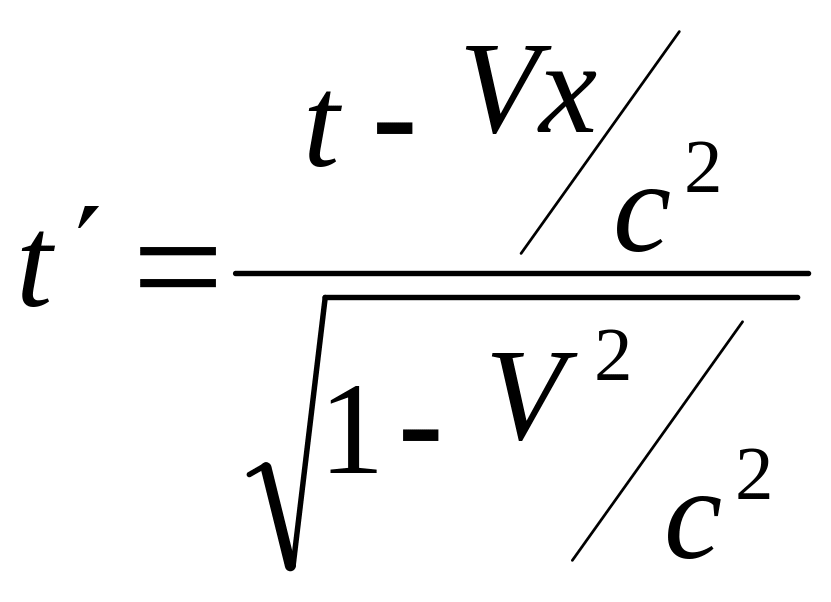.(12.1)

Принципиально новым в преобразовании Лоренца по сравнению с преобразованием Галилея является то, что время в системе отличается от времени в системе . Инвариантность скорости света обеспечивается в результате отказа от абсолютного характера времени.

Пример №1. Рассмотрим два события, происходящие в одной точке системы в моменты и . В системе в точке соответствующие моменты времени представляются в виде

,

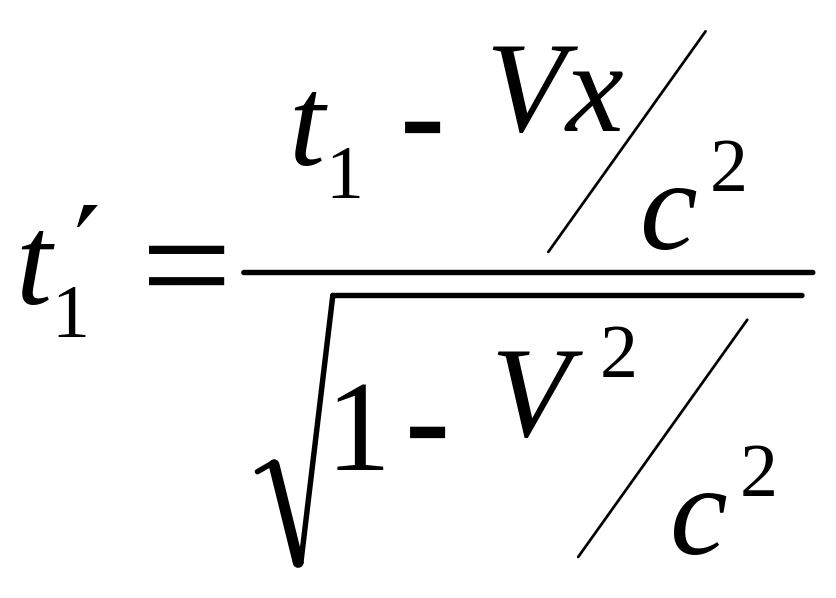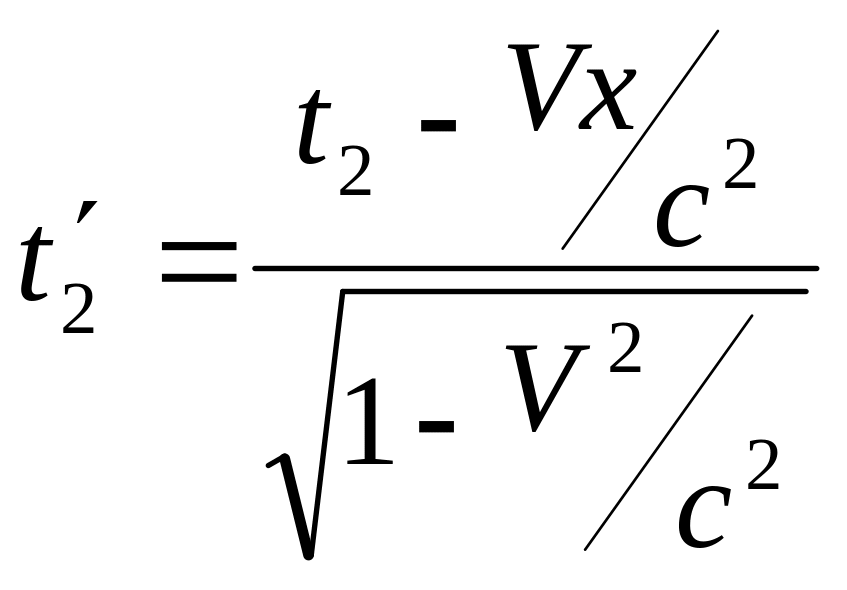
и промежутки времени между событиями в двух системах связаны соотношением

,

показывающим, что эти промежутки времени отличаются. Отметим важное обстоятельство. Промежуток времени в системе определяется по одним часам (эти часы находятся в точке ). Показания времени и определяются по двум различным, разнесенным в пространстве часам и .

Пример №2. Рассмотрим длину отрезка (стержня) в двух инерциальных системах отсчета. Пусть стержень длиной покоится в системе . Найдем координаты концов этого стержня в системе в один и тот же момент времени . Из преобразования Лоренца имеем

.

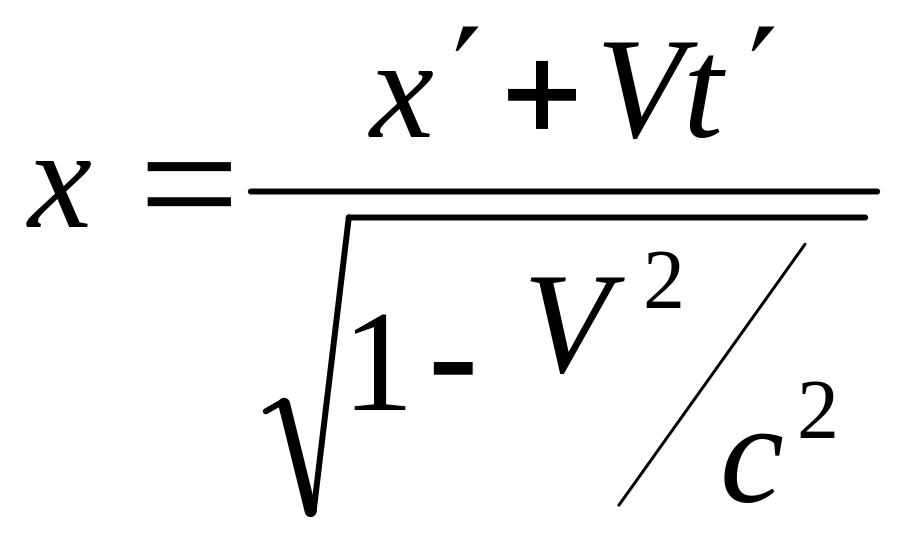Взяв , получим связь .

Наибольшую длину стержень имеет в той системе отсчета, в которой он покоится. Эту длину называют собственной длиной стержня. Уменьшение длины стержня в системе по сравнению с собственной длиной в раз называют Лоренцевым сокращением.

Из преобразований Лоренца следует соотношение ,

то есть, величина является инвариантной. В общем случае имеется инвариантность квадратичной формы . (12.2)

Представляется удобным ввести четырехмерное пространство (4 - пространство) псевдоевклидово пространство Минковского. Оно представляет совокупность точек ( ), где (четвертая координата является мнимой величиной). Точки в этом пространстве называют мировыми точками. Каждой такой точке соответствует некоторое событие. Инвариантность квадратичной формы (12.2) означает, что преобразованию Лоренца соответствует поворот системы координат в пространстве Минковского.

Получим преобразование Лоренца, соответствующее трехмерному движению системы в произвольном направлении с постоянной скоростью , . Вектор представим в виде суммы составляющей поперек направления вектора скорости и - составляющей вдоль этого направления

,

где , . Так как, поперечная составляющая вектора скорости имеет нулевую составляющую, то не происходит изменения при переходе от одной инерциальной системы к другой . Преобразование Лоренца имеет вид , , ,

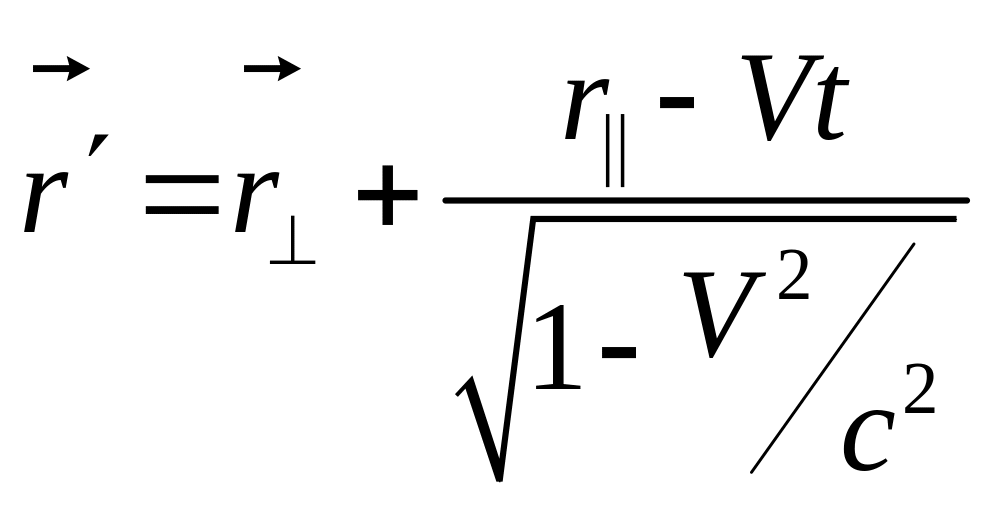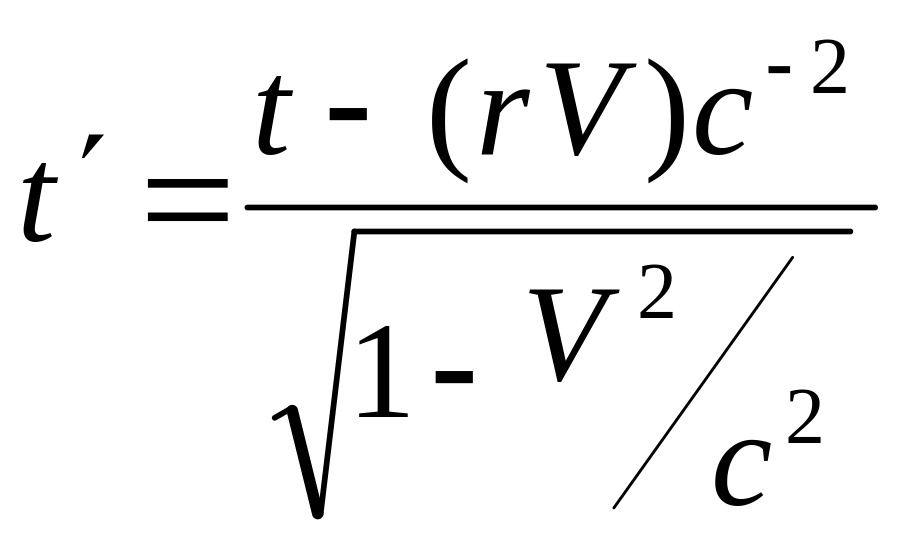Преобразования Лоренца и введение относительности понятия времени составляют основу специальной теории относительности. Эта теория была создана Эйнштейном (1905 г.), значительный вклад был сделан Лоренцем и Пуанкаре.

12.2. Интервал. Собственное время. Если рассматриваются два события и в одной системе отсчета, то согласно преобразованию Лоренца инвариантом будет величина

,

называемая интервалом между рассматриваемыми событиями: .

Иногда понятие интервал вводится иначе

Для бесконечно близких событий в системе и в системе интервалы определяются соотношениями

, .

Аналогичные определения вводятся и для интервала .

Введем понятие собственное время. Пусть часы расположены в системе и в этой системе они неподвижны: . Эта система пусть движется произвольным образом относительно системы при этом (система не является инерциальной). Однако в течении бесконечно малых промежутков времени систему можно считать инерциальной (имеет место локальная инерциальность). Относительно системы часы покоятся, значит . Возьмем бесконечно малый промежуток времени в системе и найдем соответствующий ему промежуток времени в системе . Из условия инвариантности интервала будем иметь

,

где , - скорость перемещения часов и системы относительно системы . В результате получим связь промежутков времени в двух системах:

, - произвольная функция времени. Система является локально инерциальной (инерциальной в течение времени ). Время, показываемое часами в системе, относительно которой они покоятся, называется собственным. Ниже будем обозначать его при использовании соответственно понятия интервал и . Для собственного времени имеем выражение

, .

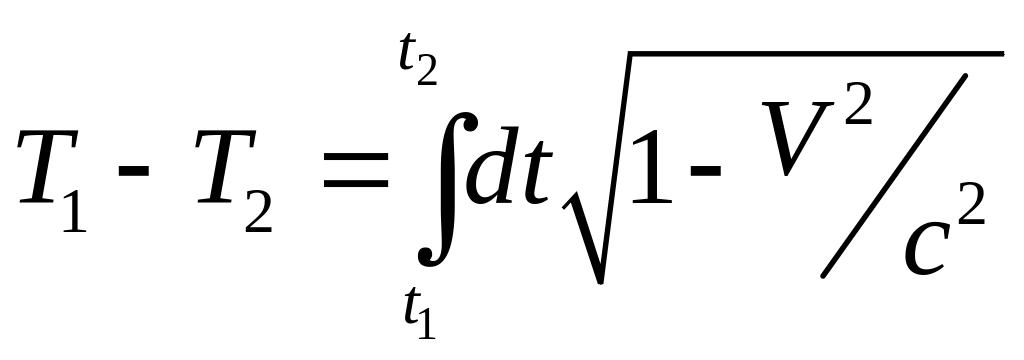Собственное время меньше, чем время в системах, движущихся относительно этих часов. Условие инвариантности интервала в рассматриваемой задаче имеет вид

, или ; , или .

Собственное время является инвариантом.

12.3 Сложение скоростей. Аберрация света (аберрация - отклонение). Трехмерные скорости частицы в системах и даются формулами

, ,

Пусть система движется с постоянной скоростью вдоль оси ( ), тогда согласно преобразованию Лоренца будем иметь

Разделив первые три равенства на четвертое, получим формулы для компонент скорости частицы

, ,

Если устремить скорость света к бесконечности, то получатся формулы сложения скоростей классической механики. Равномерное движение в одной инерциальной системе остается равномерным в любой другой инерциальной системе. Равноускоренное движение в одной инерциальной системе не является равноускоренным в других инерциальных системах. Если движение частицы происходит вдоль оси (имеет место параллельное движение частицы и системы отсчета), то правило сложение скоростей имеет вид

. (12.3)

Если взять , то получим . Скорость света обладает свойством инвариантности.

Формула (12.3) упрощается, если ввести в рассмотрение новые функции и (гиперболические тангенсы скоростей):

, .

Соотношение (12.3) принимает вид

,

т.е. при параллельном движении частицы и системы отсчета складываются гиперболические тангенсы скоростей. Использование преобразования Лоренца предполагает, что относительная скорость систем отсчета, т.е относительная скорость материальных объектов не может быть больше , так как при преобразование становится мнимым. Можно убедиться, что при произвольном движении частицы справедлива формула

.

Отсюда следует, что при произвольном движении частицы справедливо утверждение: если , то и . Скорость частиц не превосходит скорости света. Если же , то и . Определим, как изменяется направление скорости частицы при переходе из одной инерциальной системы в другую. Ограничимся случаем, когда траектория движения частицы лежит в плоскости .Обозначим через угол между

и осью . (напомним, что ), тогда

из формул преобразования скоростей получается

.

В случае получаем формулу для аберрации света (аберрация – латинское слово, означающее уклонение, заблуждение; в данном разделе подразумевается изменение направления распространения света при переходе из одной системы отсчета в другую)

. При имеем ,

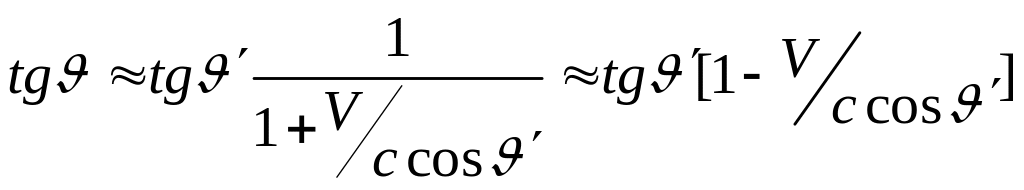
При малых значениях будет , и имеет место разложение в ряд Тейлора

и окончательно имеем описание малого изменения направления света при :

.