11. Геометрическая оптика. Учет влияния дифракционных эффектов.

11.1. Приближение геометрической оптики при распространении волн в неоднородной среде. Уравнения эйконала и переноса. Траектория луча. Принцип Ферма. Точка поворота луча. Геометрическое место точек поворота. Каустика. Лучевые трубки. Уравнение переноса. Уравнения Максвелла описывают все электромагнитные явления, в том числе и оптические. Однако, такой общий подход, как правило, очень сложен. При решении задач нужно учитывать граничные и начальные условия. Точные решения можно получить только в простейших случаях, когда задача характеризуется значительной симметрией. Имеется обширная область переменных полей, в которых уравнения Максвелла могут быть значительно упрощены. Это область очень коротких волн, когда длина волны в первом приближении полей, вообще не фигурирует. Для этого нужно, чтобы длина волны была значительно меньше всех характерных размеров задачи. В этом случае распространение электромагнитного поля происходит вдоль геометрических линий, называемых лучами. Свойства этих лучей в первом приближении не зависят от длины волны. Законы электромагнитного поля формулируются на языке геометрии. Поэтому такая ситуация носит название геометрическая (или лучевая) оптика. Следующее приближение по малому параметру учитывает волновую природу полей. Эти проявления носят общее название дифракционных явлений.

1). Рассмотрим вопрос о распространении электромагнитных волн в неоднородной изотропной среде без пространственной дисперсии и без потерь. Ограничимся случаем гармонических полей. Задача сводится к решению уравнений Максвелла для комплексных амплитуд.

Уравнение для поля получается из первых двух уравнений

Это уравнение перепишем в виде

Уравнение дает представление для . Ниже ограничимся такой поляризацией волны, что . Это позволяет получить уравнение для поля в виде

.

Рассмотрим простейший вид неоднородности среды: . Согласно условию рассматривается ситуация , (волна горизонтальной поляризации) . Поле вне источника описывается однородным скалярным уравнением

. (11.1)

Представим волновое число в виде

,

где - волновое число на уровне (выбор этого уровня произволен, он может выбираться, например, из соображений удобства написания формул), - показатель преломления неоднородной среды. Решение уравнения (11.1) будем искать в виде

. (11.1А)

Отметим, что это нелинейная замена неизвестной функции, и вместо одной неизвестной функции введено две неизвестные функции и . Это позволяет поставить дополнительное условие на новые неизвестные функции. Учитывая формулы дифференцирования

и принимая во внимание возможность постановки дополнительного условия, уравнение для и разобьем на систему двух нелинейных уравнений

(11.2)

Второе уравнение системы (11.2) называется уравнением переноса. Благодаря нелинейной замене (11.1А), система уравнений (11.2) нелинейная.

В среде без потерь и - вещественные функции, при этом - модуль функции , а - это фаза функции . Ниже ограничимся рассмотрением именно такой ситуации (среда без потерь, или с очень малыми потерями). Функцию называют оптическим путем или эйконалом («эйкон» - по – гречески «изображение», отсюда в русском языке слово «икона»). Если - характерный пространственный масштаб изменения амплитуды поля в среде, тогда справедливы оценки . Учитывая это и требуя выполнения вышеотмеченного условия или (коротковолновое приближение), в первом уравнении системы (11.2) можно пренебречь слагаемым . В результате получим уравнение для (уравнение эйконала), которое содержит только одну неизвестную функцию

(11.3)

После построения решения для эйконала на основе (11.3), второе уравнение системы (11.2) используется для нахождения амплитудной функции .

Уравнение эйконала можно получить другим способом. Покажем как это можно сделать. По существу, представление при условии, что медленно изменяющаяся функция, является описанием квазимонохроматической волны. Поэтому можно ввести понятие локального волнового числа и на основе этого определения получить уравнение эйконала (11.3). В самом деле имеет место определение локального волнового числа

(11.4)

где , и . В результате из определения (11.4) получается уравнение эйконала (11.3).

Поверхности равной фазы носят название волновых поверхностей. Будем искать решение уравнения эйконала (11.3) в виде суммы трех функций, каждая из которых зависит только от одной координаты

.

При этом уравнение эйконала принимает вид

.

В левой части этого уравнения стоят функции не зависящие от , а в правой части функции зависят от . Это может быть только в том случае, когда эти функции являются постоянными величинами.

Ведя обозначения , , получим решение в виде

.

Значение соответствует точке внутри источника. Для нахождения входящих в это выражение постоянных величин воспользуемся тем, что в малой окрестности источника среду можно считать однородной . Здесь эйконал должен совпадать с эйконалом плоской волны, распространяющейся в направлении волнового вектора

,

где - направляющие косинусы вектора . Для волны, распространяющейся в сторону увеличения значений координат, имеем

.

Вращением системы координат вокруг оси можно добиться того, что . Вместо угла введем в рассмотрение угол выхода волны (луча) . Определение понятия «луч» будет дано позже. На (Рис.11.1) , и получим представление

. (11.5)

Введем единичный вектор , ортогональный поверхностям равной фазы . В среде без потерь согласно уравнению эйконала (11.3) имеем представление . Линия, в каждой точке которой вектор касателен к ней, называется лучом. Существует другое определение луча: луч это геометрическое место точек с максимальным значением поля. Без доказательства отметим, что в изотропной среде оба определения эквивалентны. В случае анизотропных сред эти два определения дают различные лини (траектории). В каждой точке луча в изотропной среде имеем

,

где - угол между лучом и осью в данной точке луча.

С другой стороны, при учете (11.5) имеем представление для среды без потерь

.

Значит, справедливы формулы, дающие закон Снеллиуса для неоднородной среды

.

2). Получим уравнение, описывающее траекторию луча, для этого выделим элемент этой траектории. Так как , то имеет место

.

Интегрируя это соотношение, получим уравнение, описывающее траекторию луча

Уравнение луча может использоваться для различных целей.

1Оно пригодно для построения зависимости при заданном значении угла выхода луча .

2По заданным координатам точек наблюдения и источника, можно найти угол выхода луча . В этой задаче находится такой угол выхода луча , при котором луч «выйдя» из источника попадет в точку наблюдения. Следует отметить , что эта задача может иметь несколько решений: в точку наблюдения может попадать несколько лучей от одного источника.

При распространении волны в неоднородной среде происходит «искривление» луча. Возможен «поворот» луча. Точкой поворота луча в среде с зависимостью , называется наивысшая точка на траектории луча (Рис.11.2). В этой точке угол выхода луча становится прямым , поэтому . Соотношение можно использовать для нахождения высоты точки поворота луча , вышедшего из источника под углом . Горизонтальная координата точки поворота определяется интегралом

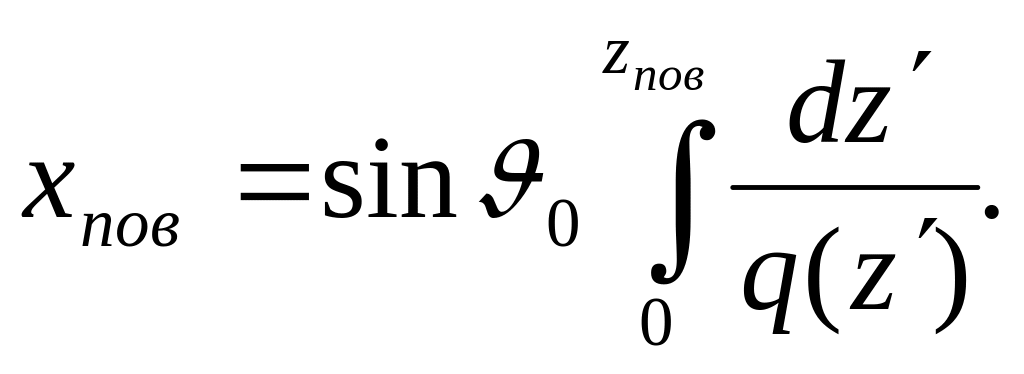
Геометро - оптическое приближение поля имеет вид

.

При расчете фазового набега интегрирование должно производиться по всей траектории луча, поэтому для луча, претерпевшего поворот, будем иметь

.

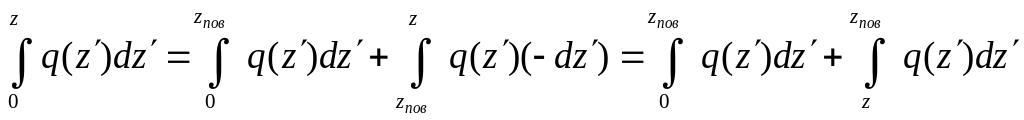3). Поле распространяется с фазовой скоростью . Поэтому элемент времени связан с элементом - элемент длины луча соотношением

.

Значит, время , затрачиваемое волной, чтобы пройти путь между двумя точками и на одном луче, определяется интегралом

.

Как отмечалось выше, могут быть несколько лучей соединяющих точки и . Здесь речь будет идти о ситуации, когда имеется один луч, соединяющий точки и .

Так как справедливо соотношение в среде без потерь: , то имеем представление для оптической длины луча . Это соотношение можно представить в эквивалентной форме

, , .

Оптическую длину можно ввести не только для реального луча, но и для произвольной кривой , соединяющей точки и :

,

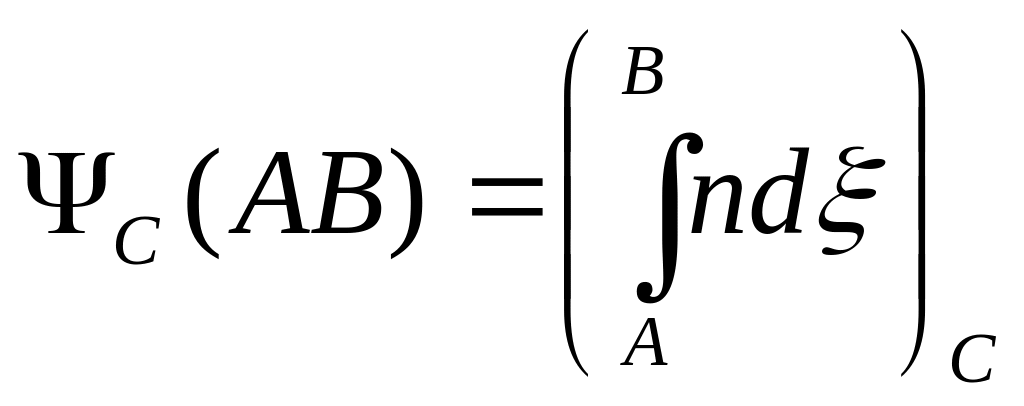где - элемент длины кривой . Оптическая длина луча может быть найдена по формуле

, .

где - угол между элементом пути вдоль луча и элементом пути вдоль кривой .По этой причине имеет место принцип Ферма, который утверждает, что оптическая длина реального луча меньше оптической длины любой другой кривой, соединяющей те же точки. При этом волна распространяется таким образом, чтобы время ее распространения было минимальным. Получается это, так как имеет место параллельность векторов , т.е. вектор ортогонален поверхности равной фазы . Поэтому

Согласно принципу Ферма вдоль реального луча укладывается минимальное (по сравнению с любой другой кривой, соединяющей те же точки) число длин волн. Это обеспечивает положительную интерференцию, или главный максимум на реальном луче.

4). Для одного луча, заданного уравнением , точка поворота (в нашей задаче это точка наибольшего или наименьшего «подъема луча») находится из решения уравнения . Геометрическое место точек поворота лучей, в зависимости от угла выхода , определяется системой двух уравнений

.

5). Искривление лучей в неоднородной среде может привести к возникновению огибающей семейства лучей (каустики). Каустика разделяет области пространства с различным числом лучей в этих областях (Рис.11.3). Каустика, в частности, отделяет часть пространства, заполненную лучами, от каустической тени (области не содержащей лучи). Уравнение описывает однопараметрическое семейство линий ( - параметр), поэтому положение каустики определяется системой двух уравнений

.

При отсутствии огибающей семейства лучей (каустики) два луча уходящие из источника под близкими углами, по мере распространения будут удаляться друг от друга. При наличии огибающей, в ее окрестности лучи будут приближаться друг к другу, если они вышли из источника под близкими углами. На каустике происходит сближение лучей (фокусировка). В окрестности каустики поле локально не плоское. Здесь нарушается приближение геометрической оптики.

6). Выясним свойства амплитуды . Для этого рассмотрим волновую поверхность равной фазы и выделим на ней малую площадку , которая пронизывается соответствующим пучком лучей. Проведем эти лучи до пересечения с другой волновой поверхностью , на которой пучок лучей выделит площадку .Объем пространства, занимаемый проходящими через площадки и лучами, называется лучевой трубкой. Займемся определением медленно изменяющейся амплитудной функцией , удовлетворяющей уравнению переноса (второе уравнение системы (11.2))

,

где эконал считаем уже найденным. Выделим участок лучевой трубки, ограниченный с торцов элементами площади и , перпендикулярными лучам в трубке, и следовательно совпадающими с поверхностями равной фазы (Рис.11.4). Введем вспомогательный вектор (рассматривается среда без потерь). Имеет место

.

Следствием является

,

где - объем выделенного участка лучевой трубки, - поверхность, ограничивающая этот объем, - единичная, внешняя по отношению к нормаль. Так как вектор ориентирован вдоль луча, то имеем

,

из которого для короткой трубки, у которой , получаем или . В лучевой трубке справедливо представление для амплитудного множителя

. (11.6)

Так как , то при (это происходит в окрестности каустики), имеет место резкое изменение функции .

11.2. Условия применимости приближения геометрической оптики. В более общем случае, решение уравнения (11.1) можно построить в виде

, Где .

Подставляя эти выражения в уравнение (11.1), и приравнивая нулю коэффициенты при одинаковых степенях , в нулевом приближении получим уравнение эйконала

,

а в следующих приближениях возникает система рекуррентных уравнений для амплитуд

,

Приближению геометрической оптики соответствует представление

.

Основное условие применимости такого приближения связано с пренебрежением в равнении (11.2)слагаемым . Это условие можно записать в виде

. (11.7)

Из (11.7) следует оценочное условие

,

Где - пространственный масштаб изменения амплитуды , - длина волны. Используем приближенное представление (11.6) ( )для медленно изменяющейся амплитуды и получим ограничения на свойства среды и частоту. Произведем оценки

,

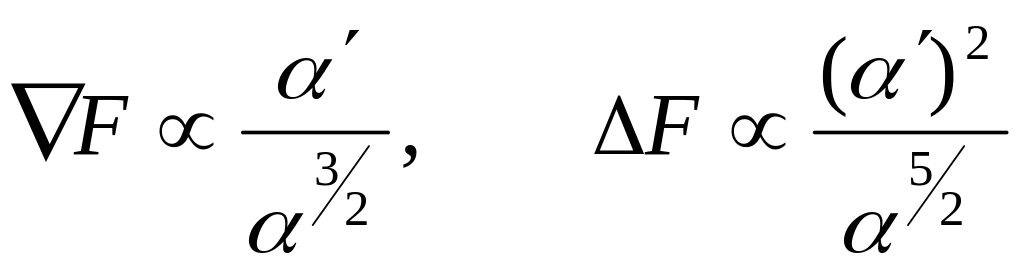условие (11.7) принимает вид 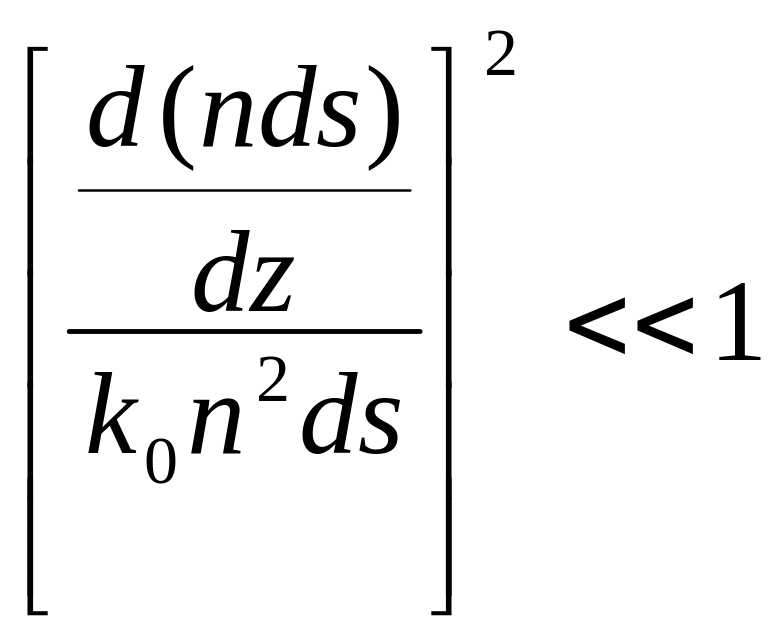, или .

Это условие нарушается там, где (в окрестности каустики) и нарушение происходит при . Приближение геометрической оптики нарушается в области, где функция изменяется резко. Так как , то условием выполнения условия применимости приближения геометрической оптики является требование малой длины волны .