6.Оптимальные смешанные стратегии
Стратегии X*> У * называются оптимальными, если выполняются неравенства:
То есть, стратегии X* Y* называются оптимальными, если их применение обеспечит игроку А средний выигрыш не менее, чем при применении им любой другой стратегии X и игроку Б средний проигрыш не больше, чем при применении им любой другой стратегии Y . Совокупность оптимальных стратегий (X*> Y*) называется оптимальным решением, а значение платежной функции - ценой игры:
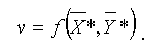
Согласно основной теореме теории игр, каждая конечная игра имеет по крайней мере одно конкретное решение, которым может быть и определена смешанная стратегия. Применение оптимальных стратегий позволяет получить выигрыш, равный цене игры.
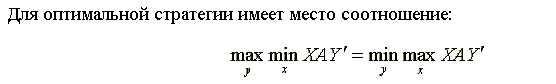
Таким образом, применение игроком А оптимальной стратегии X* должно обеспечивать ему при любых действиях игрока Б выигрыш, не менее, чем v Поэтому выполняется соотношение:
Аналогично для игрока Б. Оптимальная стратегия Y* должна обеспечить при любых стратегиях игрока А, проигрыш, не превышающий v.
-
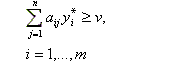
Исследование игр, заданных платежными матрицами
Вообще задача решения игры, если ее матрица не содержит седловой точки, тем сложней, чем больше значения тип. Поэтому в теории матричных игр рассматриваются способы, с помощью которых решение одних игр сводится к решению других, более простых (в частности, с помощью сокращения размерности матрицы). Сократить размерность матрицы можно, исключая дублирующие и заведомо невыгодные доминирующие стратегии.
Т.о., при решении игры, размерностью nхm следует:
– проверить, не содержит ли матрица седловой точки,
– если седловой точки нет, то сравнить между собой элементы строк и столбцов для исключения доминирующих стратегии. Исключения производить следующим образом.
1. Рассмотрим стратегии игрока А (строки). Так как игрок А стремится увеличить свой выигрыш, то можно исключить из рассмотрения (вычеркнуть) строки, в которых все элементы будут не больше соответствующих элементов некоторой стратегии (строки) Д .Эти стратегии заведомо невыгодны и игрок А никогда ими не воспользуется.
2. Теперь рассмотрим стратегии игрока Б (столбцы). Этот игрок стремится уменьшить свой проигрыш (выигрыш игрока А). По этому столбцы, которые доминируют над столбцом Bj (все элементы больше или равны элементам столбца Bj), можно тоже исключить из рассмотрения как заведомо невыгодные для игрока Б.
После этого упрощенную матрицу проверяют на наличие в ней седловой точки, что позволяет сразу же определить решение и цену игры.
Если седловой точки нет, то переходят к определению оптимальных смешанных стратегий.
Рассмотрим пример:
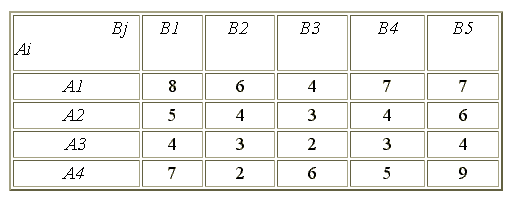
Исследовать игру, заданную платежной матрицей (см. табл. 3). Таблица 3 Платежная матрица
Решение.
1) 1-я строка доминирует над 2-й и 3-й, так как все ее элементы соответственно не меньше элементов 2-й и 3-й строк. Поэтому стратегии Д? и Аз заведомо менее выгодны, чем А\ и могут быть исключены (игрок А никогда не воспользуется этими стратегиями). В результате получаем матрицу
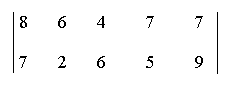
В этой матрице 1, 4 и 5-й столбцы доминируют над 2-м. Поскольку столбцы характеризуют стратегии игрока Б, стремящегося уменьшить выигрыш игрока А, то эти стратегии заведомо невыгодны.
После их исключения получаем матрицу
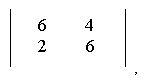
в которой нет доминирующих стратегий. Определив нижнюю и верхнюю цены игры, получим
Теорема:
Если один из игроков, применяет свою оптимальную смешанную стратегию, то его выигрыш, равен цене игры v, вне зависимости от того, с какими вероятностями другой игрок будет принимать стратегии, вошедшие в оптимальные, в т.ч. и чистые стратегии.
Согласно этой теореме, применение оптимальной стратегии х = (яд ) обеспечивает для игрока А получение выигрыша V, при любых стратегиях для игрока Б. Оптимальная стратегия для игрока Б тоже является смешанной. Поэтому, если игрок А применяет свою оптимальную стратегию, то при этом игрок Б может использовать одну из чистых стратегий и величина выигрыша игрока А останется неизменной.
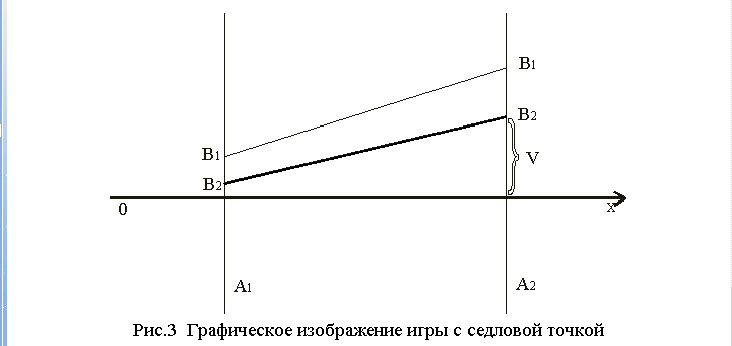
Запишем систему уравнений:
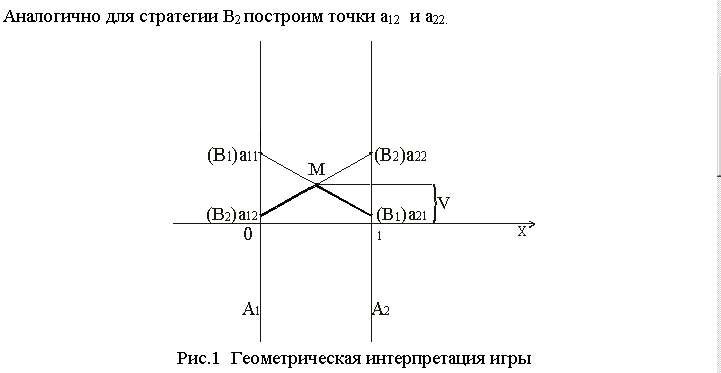
Отложим эти точки на прямых A1 и А2 . Соединим точки B1B1 и В2В2. На пересечении этих прямых получится точка М, соответствующая смешанной стратегии. Ординаты точек, лежащих на ломанной В2МВ1 характеризуют минимальный выигрыш для игрока А при использовании любой смешанной стратегии X. Следуя принципу максимина, получим, что оптимальное решение игры определяет т. М, в которой минимальный выигрыш достигает максимума. Ей отвечает на оси абсцисс оптимальная стратегия X*, а ордината равна цене игры v. По цене игры сразу находится оптимальная стратегия для игрока Б.
