с.м.чернов_квантовая механика

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Могилёвский государственный университет им. А. А. Кулешова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

главное квантовое число n =1,2,...∞;

.pdf

Скачиваний:

Добавлен:

22.03.2016

Размер:

2.6 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 208 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

§ 29. Движение электрона в кулоновском поле ядра

Пусть электрон с массой m0 движется в кулоновском поле точечного ядра заряда Ze, тогда потенциальная энергия взаимодействия электрона с ядром будет равна:

U (r) = −	Ze2	.	(29.1)
	4πε0 r

Так как поле центрально-симметричное, то координатная часть волновой функции в сферических переменных имеет вид:

где радиальная часть R(r)

Ψ(r,θ,ϕ) = R(r)Yl m (θ,ϕ) ,

(29.2)

удовлетворяет радиальному уравнению Шрединге-

ра (26.1):

h2l (l +1)

2 dR

2m0

E −U (r )−

R = 0

r dr

2m0r

или

(

1 d

)

R = 0 .

E +

−

4πε

2m0r

(29.3)

Запишем последнее уравнение в безразмерных величинах, для этого

можно использовать характерные параметры теории Бора:

4πε

= 0,528 10−10

м – первый боровский радиус;

m e

m0 e4

=13,6эВ

( E1 = −E0

– энергия основного состояния атома

2h2 (4πε

0 )2

водорода).

Для дальнейшего введем безразмерные величины:

r ;

ρ =

4πε

0 h

χ2 ≡ −

2h2 (4πε

E .

= −

m0 e

Тогда уравнение (29.3) примет вид:

d 2 R

2 dR

l(l

+1)

+ −χ

−

R(ρ) = 0 .

d ρ

ρ d ρ

(29.4)

(29.5)

Последнее уравнение имеет решение, удовлетворяющее стандартным требованиям, если выполнены два условия:

1.	χ =	Z	,	где n=1, 2, 3 ,.., называется главным квантовым числом.
		n

2.	l ≤ n −1,			т.е. l=0, 1, 2,...(n – 1).

Отсюда, с учетом обозначения (29.4), найдем энергию атома водорода:

E = En = −E0

Z 2

= −

m e4

Z 2

(29.6)

2h2 (4πε0 )2 n2 .

Полученный результат полностью совпадает с результатом боровской

теории водородоподобного атома.

Сами же решения уравнения (29.5) имеют вид:

R(ρ) = Rnl (ρ) = A(

2Z ρ

)

−Z

2l +1

(

2Z ρ

)

(29.7)

n Ln+l

где А – нормировочная постоянная, которая находится из условия:

∞∫R2 (r )r2dr =1,

и равна:

A =

+l)!

(2l +1)! 2n(n

−l −

1)! n

d m

x d n

−x

функции

(x)=

)

называются обобщенными полиномами

Ляггера.

Приведем примеры простейших радиальных волновых функций Rnl (ρ) для случая n=1,2 для атома водорода ( Z =1):

e−ρ ;

(29.8)

e−12

ρ 1 − 1

;

(29.9)

(2a0 )

e−12

ρ 1 ρ.

(29.10)

(6a0 )32

Здесь а0 – первый боровский радиус.

§ 30. Вырождение уровней энергии в атоме водорода. Спектры щелочных металлов

В предыдущем параграфе решалась задача на собственные значения:

Hψnlm = Enψnlm

для кулоновского поля (29.1). Оказалось, что собственные значение энергии En зависит лишь от одного, главного квантового числа n . Однако, собствен-

ные функции ψnlm определяются тремя квантовыми числами n,l,m , где:

орбитальное квантовое число l = 0,1,...(n −1);	(L = h l (l +1));
магнитное квантовое число m = 0,±1,±2,... ± l;	(Lz = hm).

Таким образом, одному собственному значению энергии En соответствует не-

сколько собственных функций ψnlm , т.е. в системе имеется вырождение. На-
пример, основной уровень (n =1, l = 0, m = 0) не вырожден E1 →ψ100	(k =1).
Однако, первый возбужденный уровень четырехкратно вырожден	(k = 4):
E2 →ψ200 ,ψ21−1,ψ210 ,ψ211. В общем случае кратность вырождения	равна:
n−1
k = ∑(2l +1)= n2 . Выясним природу вырождения по m и l .

l=0

Вырождение по магнитному квантовому числу m есть свойство цен-

тральной симметрии поля. Действительно, в любых центральных полях не существует физически выделенных направлений в пространстве и, следовательно, все измеряемые величины не должны зависеть от проекции Lz = hm .

При включении электрических и магнитных полей уровни энергии будут зависеть и от m, и от n (эффект Штарка в электрических полях и эффект Зеемана в магнитных полях).

Вырождение по орбитальному числу l связано с кулоновским характе-

ром взаимодействия U (r) ~ 1r (такое вырождение называется случайным, ди-

намическим вырождением). Эта особенность проявляется, в частности, в спектрах щелочных металлов Li, Na, K, Rb, Cs. В этих элементах валентный электрон движется в поле ядра, экранированного остальными (Z −1) элек-

тронами, но в этом случае суммарное эффективное поле не носит кулонов-

− r

ский характер U (r) ~ e r0 , значит, уровни энергии будут зависеть и от n , и от l : E = Enl . Схематически, это можно представить на следующей энергетической диаграмме:

Enl

3 p 3d

2 p

Энергетический

спектр H

спектр Li

Опыт показывает, что при квантовых переходах выполняются так называемые правила отбора: l = ±1; m =0,±1. Например, возможны переходы вида

3p ↔2s; 3p ↔1s , но запрещены 3p ↔2p; 3d ↔1s .

§ 31. Радиальная и угловая плотности электронных облаков в атомах

В соответствии с физическим смыслом волновой функции вероятность того, что электрон будет обнаружен в элементе объема dV, находящийся в точке с координатами (r,θ,ϕ), равна:

dW	(r,θ,ϕ)=	ψ	nlm	(r,θ,ϕ)	2 dV.	(31.1)

nlm

Учитывая, что ψnlm (r,θ,ϕ) = Rnl (r )Ylm (θ,ϕ) и dV = r2drdΩ, для этой вероятности получаем:

dW	= R2 r2dr	Y m (θ,ϕ)	2 dΩ.	(31.2)

nlm	nl	l

Интегрируя последнее равенство по радиусу и углам, и учитывая условие нормировки:

∞			2dΩ =1,
∫Rnl2 r2dr =1,	∫	Ylm		(31.3)
∫Rnl2 r2dr =1,	∫	Ylm		(31.3)
0

можно отдельно рассмотреть распределение положения электрона по радиусу

иуглам.

1)Распределение электронной плотности по радиусу.

Из (31.2) после интегрирования по углам, можно найти плотность вероятности обнаружения электрона на расстоянии r от ядра:

w	=	dWnl	= R2	(r)r2 .	(31.4)
		dr
nl			nl

Для примера, рассмотрим радиальное распределение электронов для

основного (1s) и первого возбужденного (2s) состояний атома водорода.

Учитывая вид радиальных волновых функций Rnl (r) (29.8) и (29.9), для wnl (r) получаем (а0 – первый боровский радиус):

w10 = 43 e−2 a0 r2 , (31.5)

		1		−	r						r	2
		1		−	a			2			r	2
w20	=			e	0		r		1	−		.	(31.6)
w20	=		3	e	0		r		1	−		.	(31.6)
		2a0									2a0
						74

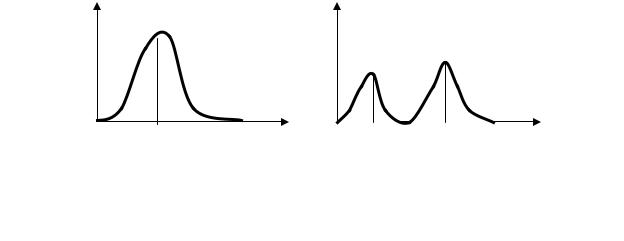
Функция w10 имеет максимум плотности в точке r = a0 , а w20 имеет две экстремальные координаты: r1 = 0,8a0 и r2 = 5,2a0 . Графики зависимости wnl (r) изображены на рисунке 11.

0	a0	r	0 0,8a0	5,2a0	(	r
	Рис. 11. Радиальная плотность электронов для основного				(	)
	Рис. 11. Радиальная плотность электронов для основного				1s

и возбужденного (2s) состояний

Таким образом, распределение электронов размазано в пространстве с максимальной плотностью при r = a0 для основного состояния, что частично

согласуется с теорией Бора. Однако первое возбужденное состояние ничего общего с боровской теорией не имеет.

2) Распределение электронных облаков по углам.

Интегрируя (31.2) по всем расстояниям, можно ввести плотность вероятно-

сти обнаружения электрона в направлении углов (θ,ϕ):

(θ ,ϕ ) =

dWlm

Y m (θ ,φ )

P m (cosθ )

2 .

(31.7)

d Ω

Следовательно, wlm не зависит от угла ϕ , и распределение по углам симмет-

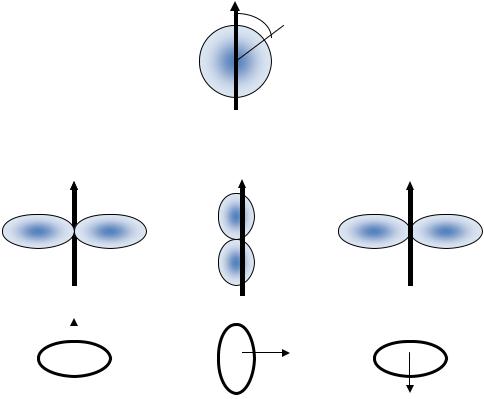
рично относительно вращения вокруг оси Z . Приведем примеры углового распределения электронных облаков для s - и p -состояний (l = 0,1) в поляр-

ных координатах (для сравнения, укажем также соответствующие боровские орбиты). Для этого учтем примеры шаровых функций (26.12).

а) 1 s -состояние электрона (l = 0, m = 0).

Такое состояние в теории Бора не существует. В квантовой же механике мы получим шарообразное распределение:

w00 P00 (cosθ ) 2 = const.

Z θ

b) 2 p -состояние электрона (l =1, m = 0,±1).

sin

θ;

−1

sin

θ.

w11 P1

(cosθ)

w10 P1

(cosθ)

cos

w1−1 P1

(cosθ)

		L
		L
m =1	m = 0	m = −1

Заметим, что форма электронных облаков определяется орбитальным квантовым числом l , а его ориентация в пространстве – магнитным квантовым числом m .

§ 32. Круговые токи в атоме и магнитный момент орбитального движения электрона

Состояние электрона в атоме водорода описывается волновой функцией

вида:

Ψ	n lm	( r ,θ ,ϕ ) = R	n l	( r ) P m (co s θ ) e imϕ .	(32.1)
	n lm		n l	l

Зная волновую функцию, можно вычислить плотность электрических токов, создаваемых пространственным движением электронных облаков, которая, в соответствии с формулой (17.9), равна:

J = −ej = −	eh	*	(32.2)
		(Ψ Ψ − Ψ Ψ*) .
	2m i	(Ψ Ψ − Ψ Ψ*) .
	0

Так как волновая функция определена в сферических координатах, то и оператор Гамильтона запишем в этих переменных:

= i		∂	+ i	1 ∂	+ i		1 ∂	(32.3)

	r ∂r			θ r ∂θ		ϕ r sinθ ∂ϕ

Тогда проекции плотности тока J на радиус, меридиан и вдоль широтных кругов равны, соответственно:

Jr = −		eh	(Ψ		* ∂Ψ − Ψ ∂Ψ* ),
	2m0i
					∂r			∂r
Jθ = −		eh		(Ψ* ∂Ψ			− Ψ	∂Ψ* ),

		2m0ir				∂θ		∂θ
Jϕ = −		eh					* ∂Ψ		∂Ψ	*
						(Ψ		− Ψ		).
		2m0ir sinθ					∂ϕ		∂ϕ

Так как радиальная функция Rnl (r) и полиномы
действительными функциями, то,					очевидно,			Jr = Jθ		= 0.

(32.4)

Plm (cosθ) являются Таким образом, в

стационарном состоянии атома токи текут вдоль широтных кругов вокруг оси Z , плотность которых легко рассчитать, используя волновую функцию

(32.1):

Jϕ = −

2im

Ψ nlm

2 = −

ehm

Ψ nlm

2 . (32.5)

2m0ir sin θ

m0 r sin θ

Полученный результат позволяет определить магнитные свойства ато-

мов, в частности, рассчитать орбитальный магнитный момент электрона. С

точки зрения электродинамики, любой замкнутый ток силой I , охватывающий плоскую площадку S с внешней нормалью n , эквивалентен магнитному моменту μ , который определяется соотношением:

μ = ISn.

(32.6)

В нашем случае мы имеем сложное пространственное распределение электрических зарядов в электронном облаке. Поэтому, разобьем весь объем атома на тонкие трубки тока сечением dσ , текущие вокруг оси Z . Величина

тока в трубке dI = Iϕdσ , а охватываемая площадка равна S =πr2 sin2 θ . Тогда z-я проекция магнитного момента выделенной трубки тока равна:

dμ

=dI S = I dσ πr2 sin2 θ =−

ehm

dσπr2 sin2 θ

nlm

m0rsinθ

(32.7)

=−

ehm

dσ 2πrsinθ

=−

ehm

2 dV.

2m0

nlm

2m0

nlm

Здесь dV = dσ 2πr sinθ – объем трубки тока. Так как магнитные мо-

менты всех трубок тока направлены вдоль оси Z , тогда полный магнитный момент будет равен:

μz = ∫d μz

= −

ehm

∫

Ψ nlm

2 dV = −

ehm

= −M Вm ,

(32.8)

где введено обозначение для одной из важнейшей для атомной физики величины, которая называется магнетоном Бора:

M В =	eh	= 0,927 10−23 Дж .	(32.9)
	2m0
		Тл

Запишем последнее выражение в векторном виде. Учитывая, что Lz = hm получим:

μ		= −	e	L .	(32.10)
	z
				z
			2m0

В силу произвольности выбора оси Z , последнее равенство можно записать в векторном виде:

μl = −	e	L	.(32.11)

	2m0

Аналогичная формула имеет место и в классической физике, однако в кван-

товой физике векторы L , μl принимают дискретные значения:

μl =−	e	h l(l +1) =−MB l(l +1), l=0, 1, 2, ...,	(32.12)

	2m0

μ =−	e	hm=−M m,	m=0±1±...±l .

lz		B
	2m0

§ 33. Экспериментальное обоснование наличия спина электрона

Как уже отмечалось, состояние электронов в атомах определяется тремя квантовыми числами (n,l,ml ). Однако, для описания всех свойств атома не-

обходимо вводить четвертое квантовое число, имеющее смысл собственного механического момента, называемый спином (to spin – вращаться). Впервые эта идея была выдвинута Паули. Представление спина как вращение электрона вокруг своей оси и сам термин “спин” выдвинули Уленбек и Гаудсмит (1925 г.). Строгую теорию спина можно построить лишь в рамках релятиви-

сткой квантовой механики, основанной на уравнении Дирака.

Из-за отсутствия траектории электрона невозможно непосредственно определить явление вращения самого электрона. Однако, наличие собственного механического момента (спина) должно приводить к появлению соответствующего спинового магнитного момента μs , который, по аналогии с

орбитальным моментом, прямо пропорционален механическому моменту S :

μs = −αS ,

(33.1)

где α – коэффициент пропорциональности, определяемый опытным путем. Продолжая эту аналогию, будем считать, что величина спина может принимать следующие значения:

	S = h s(s +1);	(33.2)
	Sz = hms ,
где s
	– квантовое число спина, подлежащее экспериментальному определе-
нию,	а ms = −s,..., s – спиновое магнитное квантовое число,	принимающее
(2s +1) дискретное значение. Отметим, наконец, что, если магнитный момент
любой природы μ поместить в магнитное поле с индукцией B , то их энергия
взаимодействия равна:
	U = −μ B.	(33.3)

Рассмотрим два фундаментальных опыта, которые являются экспериментальным обоснованием наличие спина электрона.

1) Опыт Штерна и Герлаха.

Справедливости ради следует отметить, что этот опыт впервые спроектирован Капицей и Семеновым. Сущность опыта состояла в пропускании узкого пучка атомов серебра через неоднородное магнитное поле. В этом опыте были использованы атомы серебра по следующим соображениям: во-первых, атом является электронейтральной системой, на которую не действует сила Лоренца, маскирующая взаимодействие магнитных моментов с полем; вовторых, атом серебра имеет единственный внешний валентный электрон, находящийся в s -состоянии. Следовательно, у этого атома отсутствует орбитальный момент, значит μa = μs . При прохождении атомов серебра через не-

однородное магнитное поле, направленное вдоль оси Z : Bz = B(z), атомный

магнитный момент взаимодействует с этим полем с энергией (33.3): U = −μs B = −μsz B(z), что приводит к появлению силы:

F = F = −

∂U

= μ

∂B .

(33.4)

∂z

sz ∂z

Так как μsz

принимает (2s +1) различных значений, то на экране должно об-

разоваться

(2s +1) посеребренные пятна, как показано на рисунке:

1 и m = ± 1

В этом опыте оказалось, что 2s +1 = 2 , следовательно s =

. Таким

образом, спиновые параметры электрона принимают следующие значения: 79

S =h s(s +1) =			3	h,

			4
Sz =±	h	.	(33.5)


2

Измеряя величину отклонения атомов по крайним точкам на экране,

можно рассчитать силуFz , и для заданного градиента поля ∂∂Bz определить

величину μsz . Опыт показал, что

μsz

= M B =

= α

следовательно,

2m0

коэффициент пропорциональности α =

, т.е. условие (33.1) принимает вид:

= −

S .

(33.6)

Сравнивая этот результат с формулой (32.11), можно сделать вывод, что отношение магнитного момента к механическому вдвое больше для спина, чем для орбитального момента.

2) Дублетная структура спектров паров щелочных металлов.

Рассмотрим структуру уровней энергии атома Na (Z =11) и их запол-

нение электронами.

При

возбуждении

атома

Na ва-

Enl

лентный

электрон переходит в

3p-сос-

тояние, а затем возвращается в основное

3s-состояние и излучает квант света, со-

2 p

ответствующий желтой линии спектра.

Однако

экспериментально наблюдается

не одна,

две

линии с

длинами волн

λ1 =5890 A

λ2 = 5896

A. Это можно

объяснить наличием двух энергетических уровней 3 p1 и 3p2 , каждый из которых не совпадает с 3d -состоянием. При этом

3s -уровень остается одиночным. Дальнейший анализ показал, что этот резуль-

тат носит общий характер: все уровни энергии с l ≠ 0 имеют дублетную струк-

туру. Следовательно, помимо кулоновских сил на электроны должны действовать дополнительные силы иной природы.

Указанное расщепление можно объяснить, введя дополнительное, спинорбитальное взаимодействие. Рассмотрим качественно эти силы в рамках полуклассической теории. Выберем неинерциальную систему отсчета, связанную с электроном. В этой системе координат электрон неподвижен и его орбитальные моменты μl ,L равны нулю. Однако электрон обладает спино-

<<< < Предыдущая 1 2 3 4 5 6 78 / 208 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.04.2015501.2 Кб566решебник.docx
#
18.04.201513.95 Кб13россия.docx
#
11.07.201913.89 Mб14Рубинштейн С.Л. Основы общей психологии.rtf
#
22.08.201930.64 Кб5русский СЕЛЕЗНЁВА(ТРХ-111).docx
#
25.09.201969.55 Кб7с группы.docx
#
22.03.20162.6 Mб61с.м.чернов_квантовая механика.pdf
#
18.04.2015197.73 Кб38савицкая .docx
#
18.04.2015173.57 Кб13Сведения о родителях 2014-2015.doc
#
18.04.2015447.02 Кб13Сельский туризм.pdf
#
15.08.201956.85 Кб0сем1.docx
#
11.11.2019243.71 Кб9Семаго содер и организ.doc