Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Могилёвский государственный университет им. А. А. Кулешова

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

с.м.чернов_квантовая механика

.pdf

Скачиваний:

Добавлен:

22.03.2016

Размер:

2.6 Mб

Скачать

☆

<<< < Предыдущая 12 / 202 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

3.Фотоэффект прекращается, если частота излученияω ≤ ω0 , где ω0 зависит от материала вещества и называется красной границей фотоэффекта.

Каждый металл характеризуется работой выхода А, отражающая процессы взаимодействия электронов с кристаллической решеткой (А~1эВ). Тогда можно записать закон сохранения энергии для фотоэффекта в виде (урав-

нение Эйнштейна ):

	mv2
hω = A +	max	.	(4.1)
	2

Уравнение (4.1) объясняет все эмпирические законы Столетова. Замечание. Как и любой материальный объект, фотоны должны обла-

дать и определённым импульсом:

p =	E	= h	ω	= hk ,	(4.2)
	c		c

где k = ωc = 2λπ – волновое число. Можно (4.2) записать и в векторном виде:

p = hk . При ударе фотона о препятствие, его импульс должен измениться, что должно приводить к появлению силы светового давления. Экспериментально явление давления света изучалось Лебедевым (1900 г).

§ 5. Эффект Комптона (1922)

Доказательство корпускулярной природы света может служить также прямое взаимодействие фотонов с электронами в эффекте Комптона (Нобелевская премия – 1927 г.).

Эффект Комптона состоит в изменении длины волны рентгеновского излучения, рассеянного на свободных электронах. На основании законов со-

хранения энергии и импульса для системы фотон + электрон можно записать:

				hω + m c2 = hω + mc2 ;		(5.1)
				0	0	(5.1)
				0	0
	m0			hk0	= hk + mv,
где m =	m0			. Предполагается, что первоначально электрон покоился и ско-
где m =
1		−	v2
1		−	c2
			c2

рость движения электрона после удара v ~c. Из уравнений (5.1) можно вычислить сдвиг длины волны рассеянного света

λ = λ −λ = 2Λ sin2 θ		,	(5.2)
0	2
	2

где Λ = 2πh = 2,42 10−12 м – комптоновская длина волны электрона.

m0c

§ 6. Гипотеза де Бройля о корпускулярно-волновой природе микрочастиц

Существует две группы опытов, в которых свет проявляет либо волновые, либо корпускулярные свойства.

1. Волновые свойства наблюдаются в таких опытах, как интерференция, дифракция, поляризация. В этом случае вводят такие волновые парамет-

ры, как ω,k,T , A и т.д.:				2π
ω =	2π	;	k =		.	(6.1)

	T			λ
Сам же волновой процесс можно описать в виде простейшей модели
плоских волн:
ψ (r,t )= Ae−i(ωt−k r).						(6.2)

2. Корпускулярные свойства света проявляется в таких опытах, как излучение абсолютно черных тел, фотоэффект, эффект Комптона и т.д. При таком представлении света в виде потока корпускул (фотонов) наиболее важ-

ными характеристиками являются E,p, m....
Единство этих свойств можно записать в виде:
E = hω;	p = hk;	m =	E	=	h	ω .	(6.3)
E = hω;	p = hk;	m =	c2	=	c2	ω .	(6.3)
			c2		c2

В частности, свободное движение фотонов, обладающих как волновыми, так и корпускулярными характеристиками, формально можно записать в виде:

−	i	(Et−p r )	.	(6.4)

ψ (r,t )= Ae h

Эту корпускулярно-волновую идею Луи де Бройль (1924) распространил не только для света, но и для всей материи (Нобелевская премия – 1929). В частности, последнее соотношение следует понимать как свободное движение электронов с энергией Е и импульсом p , обладающие свойствами пло-

ской волны (плоская волна де Бройля). Таким образом, должны существовать такие эффекты, которые можно интерпретировать, приписав электрону такие волновые параметры, как:

ω =	E	;	k =	p	;	λ =	2πh	=	h	.	(6.5)
	h			h			p
									mv

Для “планирования” таких экспериментов (например, дифракция), оценим порядок длины волны де Бройля в стандартных условиях при прохождении электронов в электрическом поле с разностью потенциалов U~100 В. В таком поле электрон приобретает скорость, которая находиться из условия:

eU = mv2	ϑ =	2eU .	(6.6)
2		m

Соответствующая длина волны де Бройля будет иметь порядок

λ =	h	1		≈1,2	10−9	1	≈10−10 м.	(6.7)
	2em		U			U

Таким образом, волновые свойства электронов можно наблюдать при дифракции электронных пучков на монокристаллах, имеющие период решетки а ~ λ ~ 10−10 м. Эффект дифракции в таких опытах впервые наблюдали Дэвидсон и Джермер (1927) (Нобелевская премия – 1937), а также при прохождении “электронных волн” через поликристаллические пленки (Томсон – Тартаковский, 1928 г.).

Заметим, что корпускулярно – волновые свойства присущи не только электронам. Например, Штерну и Эстерману удалось наблюдать дифракцию атомов гелия и молекул водорода при отражении от кристаллов LiF. В современной технике получили широкое распространение электронные, протонные и даже ионные микроскопы, имеющие разрешение на атомном уровне.

§ 7. Волновой пакет. Соотношения неопределенности Гейзенберга

Возникает естественный вопрос о физической интерпретации гипотезы де Бройля, кроме формальных соотношений (6.4) и (6.5). Для простоты, рассмотрим распределение волн де Бройля в пространстве для одномерного слу-

чая (вдоль оси х). Для свободного движения частицы с энергией				E0 = hω0 и
импульсом p0 = hk0 , ее состояние описывается функцией:
ψ (x,t )= A0e−i(ω0t−k0 x) .				(7.1)
Областью определения функции (7.1) является вся числовая ось, в част-
ности, во всем пространстве и во все времена	Ψ(x,t )	2 = A2	= const.

		0

С другой стороны, микрочастица (например, электрон) с корпускулярной точки зрения не может иметь бесконечные размеры, “размазанные” по всему пространству. Тогда волновые и корпускулярные представления тре-

буют решение основного вопроса: как образовать волновой процесс, имеющий ограниченное протяжение в пространстве?

Эту проблему можно решить, взяв не одну плоскую волну де Бройля, а
сумму таких волн с разными наборами k из интервала [k0 − k, k0 +				k], кото-
рую будем называть волновым пакетом:
	k	+	k
Ψ(x,t )=	0	∫	A(k)e−i[ω(k )t−kx]dk .	(7.2)
	k0 −		k
Для полного решения задачи необходимо задать зависимость от к ам-
плитуд различных волн де Бройля		A(k) и закон дисперсии ω(k) . Однако, мы

максимально упростим задачу: будем считать амплитуду всех волн одинако-

выми А(k) = A0 =const и “сделаем моментальную фотографию” пакета в момент t=0. Тогда соотношение (7.2) примет вид:

	k	−	k
Ψ(x, 0)=	0	∫	A0eikxdx = B(x)eik0x ,	(7.3)
	k0	+Δk

где амплитуда волнового пакета B(x) является функцией координаты х и равна:

B(x) = 2A0

sin kx

Для удобства введем обозначение:

kx.

ξ =

Тогда B(ξ) = 2A0

sin ξ

и, в частности

Ψ(x,0)

2 =

B( x )

2 ~ sin2ξ

ξ2

B (ξ )

(7.4)

(7.5)

(7.6)

−3π

−2π

−π

2π

3π

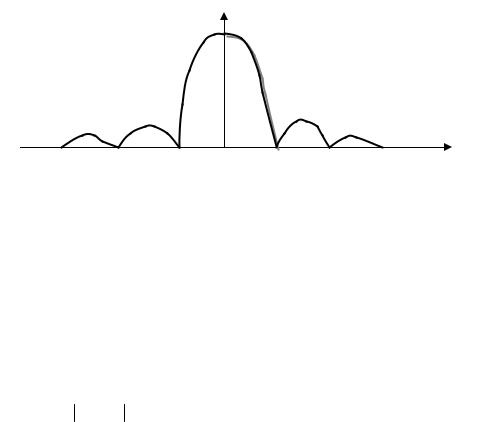
Рис. 3. Распределение волнового пакета в пространстве

Из рисунка видно, что волновой пакет ограничен в пространстве, и, в основном, сконцентрирован в области главного максимума (−π ≤ ξ ≤ π) ширины ξ = 2π . С учетом вторичных максимумов ξ = 4π и т.д. Во всяком случае, мы приходим к неравенству:

ξ = k x ≥ 2π .

(7.7)

Всвязи с теорией волновых пакетов были высказаны две идеи:

1.Функция Ψ( x,t ) 2 описывает внутреннюю структуру микрочастицы,

например, плотность распределение массы внутри самого электрона (Шредингер), причем скорость движения частицы v совпадает с групповой скорости пакета υg =υ .

Однако, эта идея несостоятельна по многим причинам: во-первых, если электрон состоит из набора различных волн де Бройля, то при дифракции они должны распространяться по разным направлениям. Во-вторых, расчеты по-

казывают, что даже в свободном пространстве волновые пакеты расплываются, удваивая свои размеры за время порядка 10−16 с, из-за различия фазовых скоростей разных волн де Бройля.

2. В этой связи Макс Борн предложил другую интерпретацию волнового пакета (Нобелевская премия – 1954), которая является общепринятой в настоящее время.

Волновой пакет описывает не внутреннюю структуру самой частицы, а ее движение, как целое, в пространстве. Причем это движение подчиняет-

ся вероятностным законам, а именно, Ψ(r,t )2 dV пропорционально вероятности нахождения частицы в элементе объема dV, расположенного в точке

rв момент времени t.

Вчастности, для одной плоской волны де Бройля нахождение частицы в

любой точке пространства является равновероятным A0 2 = const.

Вернемся, однако, к неравенству (7.7),		которое с учетом равенства
p = hk , приводит к соотношениям вида:
x	px ≥ 2πh;	(7.8)
y	py ≥ 2πh;

z pz ≥ 2πh.

Неравенства (7.8) называются соотношениями неопределенности Гей-

зенберга (Нобелевская премия – 1932). Важно подчеркнуть, что соотношения неопределенности, как следует из вывода, являются прямым следствием кор-

пускулярно-волновых свойств материи. Эти ограничения указывают на прин-

ципиальную невозможность сохранения всех атрибутов классических понятий частиц и волн в рамках единой теории. В частности, они указывают на невозможность введения даже понятия “траектории” микрочастиц в классическом понимании. Взаимоисключающие свойства “чистых” волн и частиц будут приводить в некоторых случаях к принципиальной невозможности измерения нескольких физических величин одновременно, невзирая на успехи современной экспериментальной физики.

ГЛАВА II

Математический аппарат квантовой механики

§ 8. Основные “постулаты” квантовой механики

Квантовую механику, как учебный предмет, до сих пор нельзя считать окончательно методически обоснованной дисциплиной. Поэтому разные авторы учебных пособий, включая классиков науки, предлагают различные наборы основных положений квантовой механики, которые могут служить базой для построения теории. В данном пособии приводимые основные “по-

стулаты” следует рассматривать лишь как одну из возможных версий,

имеющее экспериментальное “обоснование”.

Постулат 1. Свободное движение микрочастицы с импульсом p и

энергией E описывается плоской волной де Бройля
ψ p (r , t ) = A e − hi (E t −p r ).	(8.1)

Постулат 2. В общем случае, состояние любой квантовой системы описывается комплексной функцией координат и времени ψ (r,t), , которую будем называть волновой функцией.

Постулат 3. Согласно М. Борну, утверждается, что ψ (r,t )2 dV про-

порционально вероятности обнаружения микрочастицы в элементе объема dV в момент времени t .

Постулат 4. Волновая функция ψ (r,t) должна удовлетворять сле-

дующим 4-м условиям: а) однозначность;

б) конечности при всех r и t ;

в) непрерывность по координате; г) непрерывности 1-ой производной по координате (если потенциаль-

ная энергия не испытывает бесконечных скачков).

Эти требования в дальнейшем будем называть стандартными условия-

ми.

Постулат 5. Если квантовая система может находиться в состоянии с волновыми функциями ψ 1 (r , t ), ψ 2 (r , t ), ... , то она может также нахо-

диться и в состоянии с волновой функцией
ψ (r,t)= ∑ckψk (r,t).	(8.2)

Замечание 1. Физический смысл волновой функции.

Обозначим через dW – вероятность нахождения микрочастицы в эле-

менте объема dV в момент времени t

(∫dW =1). Тогда согласно постулату

№ 3

ψ (rr,t)

2 dV = cdW . Проинтегрируем это равенство по всему простран-

ству

∫

2 dV = c∫dW = c ,

тогда

наша вероятность будет равна

2 dV

dW =

∫

2 dV

Пусть выполняется условие нормировки:

В этом случае dW =

2 dV .

∫

2 dV =1.

Введем величину w = dV =

ψ (r,t)

=ψ ψ , которую назовем плотностью ве-

роятности.

Отсюда следует физический смысл волновой функции: квадрат модуля нормированной волновой функции есть плотность вероятности обнаружения частицы в точке r в момент времени t .

Замечание 2. Принцип суперпозиции состояния.

Волновая функция определяется неоднозначно, а с точностью до произвольной постоянной с, т.е. ψ и ψ′ = cψ – физически эквивалентны. Действительно, вычислим вероятность нахождения частицы в элементе dV:

dW ′ =

ψ′

2 dV

= dW .

∫

ψ′

2 dV

2 ∫

2 dV

∫

2 dV

Пусть квантовая система находится в состоянии с волновой функцией ψ = ∑ckψ k , тогда при измерении над этой системой мы обнаружим старые

k
состояния ψ1 , либо ψ 2 , либо ψ 3 …. При этом			cn	2 – определяет вероят-
состояния ψ1 , либо ψ 2 , либо ψ 3 …. При этом			cn	2 – определяет вероят-
ность нахождения состояния ψn , причем ∑	ck	2 = 1 . Обоснование последне-
ность нахождения состояния ψn , причем ∑	ck	2 = 1 . Обоснование последне-
k
го утверждения будет дано ниже.

{a1 , a2 ...an }

§ 9. Средние значения физических величин

Замечание. Среднее значение случайных величин.

Пусть имеется случайная величина a , которая может принимать дискретный ряд значений с вероятностями {w1 , w2 ,...wn } , при-

		n
чем, выполняется условие нормировки ∑wk			=1 . Тогда среднее значение
величины < a > равно:		k =1
величины < a > равно:		n
		n
< a >= ∑ak wk
		k =1
Если же a принимает непрерывный ряд значений из интервала [b,c] и
распределена с плотностью вероятности w(a) , так что ∫c				w(a)da =1 . Тогда
			b
< a >= ∫c aw(a)da .
b
Если плотность вероятности не нормирована, то
< a >=	∫c	aw(a)da
	b		.
	c		.

∫w(a)da

Рассмотрим средние значения основных физических величин:

1) Среднее значение координаты микрочастицы. Оператор координа-

ты.

Для простоты рассмотрим одномерную задачу, когда состояние квантовой системы описывается нормированной волновой функцией ψ ( x ) :

+ ∞

+∞

2 d x = 1 . Тогда среднее значение

< x >= ∫ xw( x)dx .

∫

ψ ( x )

− ∞

−∞

Из физического смысла волновой функции следует, что плотность веро-

ятности обнаружения частицы в точке x равно:

w( x) =

ψ ( x)

2 ,

тогда

+∞

(9.1)

< x >= ∫ xψ * (x )ψ (x )d x =

∫

ψ * x ψ d x

−∞

где

– оператор x-координаты.

x = x

		ψ ( r ) d V .
В трехмерном случае < r > = ∫ψ * ( r ) r
В общем случае среднее значение от функции координаты вычисляется
по формуле:
	U ( r ) > = ∫ψ
<		* U ( r )ψ d V .	(9.2)
2) Оператор импульса.
Пусть микрочастица	свободно движется вдоль оси X с импульсом
px = p = const , py = pz = 0.	В соответствии с гипотезой де Бройля состояние

− i (Et−p x)

такой частицы описывается плоской волной вида ψp (x,t) = Ae h x . Так

как при свободном движении импульс не меняется, то

< px >= px = const .

Последнее соотношение справедливо, если среднее значение импульса вычислять по формуле, аналогичной среднему значению координаты:

	+∞
	∫ψ p
< px >=	∫ψ p		p x ψ p dx
	−∞				,
	+∞				,
	∫	ψ p		2 dx
	∫	ψ p		2 dx
	−∞
						∂
где оператор проекции импульса имеет вид:				p x = −ih		∂	.
где оператор проекции импульса имеет вид:				p x = −ih			.
						∂x

Докажем это утверждение. Преобразуем вначале выражение:

∂

−

(Et−px x)

= −ih

Ae h

= −ihψ

(

x ) = p ψ

∂x

px +∞∫

x .

ψ p

2 dx

Тогда среднее значение < px

−∞

= px .

+∞

∫

2 dx

−∞

Таким образом, операторы проекций импульса должны иметь вид:

∂

p x

= −ih

;

p y

= −ih

;

p z

= −ih

∂x

∂y

∂z

или в векторном виде:

p = −ih ,

(9.3)

(9.4)

где = i ∂∂x + j ∂∂y + k ∂∂z – оператор Гамильтона (набла). 19

3) Оператор момента импульса.

В механике вводится момент импульса, согласно условию L = r ×p .

Тогда в квантовой механике логично определить оператор момента импульса в соответствии с уравнением:

Lﬂ = r$ ×pﬂ

= −ihr$ × = −ih

;

(9.5)

∂

∂x

∂y

∂z

∂

L x = − i h ( y

− z

) ;

∂ z

∂ y

y = − i h ( z

∂

− x

∂

) ;

∂ x

∂ z

∂

L z = − i h ( x

− y

) .

∂ y

∂ x

Можно ввести также квадрат момента импульса

L2 = L2x + L2y + L2z .

4) Оператор энергии (оператор Гамильтона).

H =

+U (r,t) − функция Гамильтона (гамильтониан).

= (−ih )

H =

+U (r,t)

+U (r,t) = −

+U (r,t),

(9.6)

где

∂ 2

– оператор Лапласа.

∂x 2

∂y 2

∂z 2

Общий вывод. В квантовой механике все динамические переменные

имеют операторную природу F → F , при этом измеряемыми величинами являются средние значения < F > , которые вычисляются по формулам:

< F >= ∫ψ Fψ dV – для нормированной волновой функции

	∫ψ
< F >=			Fψ dV		– для ненормированной волновой функции.
	∫	ψ		2 dV


					20

<<< < Предыдущая 12 / 202 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
18.04.2015501.2 Кб566решебник.docx
#
18.04.201513.95 Кб13россия.docx
#
11.07.201913.89 Mб14Рубинштейн С.Л. Основы общей психологии.rtf
#
22.08.201930.64 Кб5русский СЕЛЕЗНЁВА(ТРХ-111).docx
#
25.09.201969.55 Кб7с группы.docx
#
22.03.20162.6 Mб61с.м.чернов_квантовая механика.pdf
#
18.04.2015197.73 Кб38савицкая .docx
#
18.04.2015173.57 Кб13Сведения о родителях 2014-2015.doc
#
18.04.2015447.02 Кб13Сельский туризм.pdf
#
15.08.201956.85 Кб0сем1.docx
#
11.11.2019243.71 Кб9Семаго содер и организ.doc