
с.м.чернов_квантовая механика
.pdf
§ 10. Алгебра операторов
Дадим основные определения теории операторов.
Определение 1. Оператором Ffl называется правило (рецепт), по которому одной функции ϕ ставится в соответствие другая функция ψ тех же не-
зависимых переменных: |
|
|
|
|
||
|
ψ = Ffl ϕ |
(10.1) |
||||
Примеры: |
Ffl = |
|
|
|
||
ψ = ϕ |
; |
|
|
|||
ψ (x)= |
dϕ (x) |
|
Ffl |
= |
d |
. |
dx |
|
|||||
|
|
|
dx |
|||
Определение 2. Оператор Ffl называется линейным, если выполняются два условия:
Ffl |
(ϕ1 +ϕ2 )= Ffl |
ϕ1 + Ffl ϕ2 ; |
Ffl |
(c ϕ)= c Ffl |
ϕ, |
где с – произвольное число.
Определение 3. Суммой операторов Ffl и Rfl называется Gfl = Ffl +Rfl , если для произвольной функции φ выполняется условие:
(10.2)
оператор
|
|
|
|
|
|
|
Gfl |
ϕ = Ffl ϕ + Rfl ϕ |
|
|
|
|
|
|
|
(10.3) |
|||||||||
|
|
Определение 4. Произведением операторов Ffl и Rfl называется оператор |
|||||||||||||||||||||||
Gfl |
= Ffl |
Rfl , который удовлетворяет условию: |
|
|
ϕ.) |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
Rfl ϕ = Ffl |
Rfl |
ϕ |
= Ffl (Rfl |
|
|
|
|
(10.4) |
|||||||||||
чин. |
Операторы, вообще говоря, образуют алгебру некоммутирующих вели- |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
||||
|
|
Пример: Пусть Ffl |
= x$ = x; |
Rfl |
= pfl |
= −ih |
|
. |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
dx |
|
|
|
dϕ (x) |
|
|
||||
Из |
определения |
(4) |
|
имеем |
|
|
|
x$pfl |
x |
ϕ (x) = −ihx |
, |
однако, |
|||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
|
|
d |
(xϕ (x))= −ihϕ −ihx ddxϕ . |
|
|
|
|
|
|
|
|
|
dx |
|
||||||||||
pfl |
x x$ϕ (x) = −ih |
Таким образом, для произвольной функ- |
|||||||||||||||||||||||
dx |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
$ |
fl |
|
|
fl |
|
$ |
|
|
|
|
|
и, следовательно |
|
|||||
ции φ выполняется равенство (xp x |
−p x |
x )ϕ = ihϕ |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
x$pfl |
|
−pfl |
x$ |
= ih ≠ 0. |
|
|
|
|
|
(10.5) |
||||||||
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
≡[ |
Ffl , Rfl ] называется коммута- |
||||||
|
|
Определение 5. Оператор Gfl |
= Ffl Rfl |
− Rfl |
Ffl |
||||||||||||||||||||
тором, а Gfl = Ffl Rfl +Rfl F fl = {Ffl |
, Rfl } – антикоммутатором операторов Ffl |
и Rfl . |
|||||||||||||||||||||||
|
|
Примеры: Очевидно, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
$ |
fl |
|
= ih; |
|
fl |
|
fl |
|
|
= ih; |
|
$ |
fl |
|
|
|
|||||
|
|
|
|
x, p x |
|
y , |
p y |
|
z, p z |
= ih; |
(10.6) |
||||||||||||||
|
|
|
|
fl |
fl |
|
|
fl |
|
fl |
]= |
|
fl |
|
fl |
|
|
= 0. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
x |
, p y |
=[ x , |
y |
p x , |
p y |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
||
Определение 6. Если в результате действия оператора Ffl на некоторую функцию ψ в результате получается та же функция ψ, умноженная на посто-
янную λ ( Ffl ψ = λψ ), то ψ – называется собственной функцией оператора Ffl (с.ф.), принадлежащей собственному значению λ (с.з.).
Определение 7. Совокупность всех с.з. оператора Ffl называется его
спектром. Спектры бывают дискретные, непрерывные (сплошные) и смешанные.
Определение 8. Если каждому с.з. λ соответствует единственная с.ф., то спектр называется невырожденным. Если одному с.з. λ соответствует к различных с.ф. ψ1, ψ2, … ψк, то спектр называется вырожденным с кратностью вырождения к.
Определение 9. Скалярным произведением двух функций ψ и φ называ-
ется число, равное интегралу вида:
ψ |
|
ϕ ≡ ∫ψ ϕdV , |
(10.7) |
|
|||
|
|
где интегрирование проводится по всей области значений независимых переменных функций ψ и φ. Обозначение скалярного произведения в виде  ψ ϕ
ψ ϕ
введено в квантовую механику П. Дираком. В частности, условие нормировки волновой функции в этих обозначениях запишется в виде:
ψ |
|
ψ = ∫ψ ψdV = ∫ |
|
ψ |
|
2 dV =1 |
(10.8) |
|
|
|
|||||
|
|
|
Среднее значение физической величины равно:
Ffl = ∫ψ FflψdV = ψ |
|
Ffl ψ . |
(10.9) |
|
|||
|
Отметим некоторые свойства скалярного произведения, которые непосредственно вытекают из определения (9):
ψ |
|
ϕ = ϕ |
|
ψ ; |
(10.10) |
||||||||
|
|
||||||||||||
|
|
|
|
αψ |
|
ϕ =α ψ |
|
ϕ ; |
(10.11) |
||||
|
|
|
|
|
|
||||||||
ψ |
|
βϕ = β ψ |
|
ϕ . |
(10.12) |
||||||||
|
|
||||||||||||
Определение 10. По аналогии с векторной алгеброй, будем называть функции ψ и φ ортогональными, если выполняется условие:
ψ |
|
ϕ = ∫ψ ϕdV = 0 |
(10.13) |
|
|||
|
|
§11. Операторы в квантовой механике
Вквантовой механике существует следующая группа операторов, которые для произвольных функций ψ и φ определим в виде таблицы:
22
Таблица 1. Основные операторы квантовой механики
№ |
НАЗВАНИЕ ОПЕРАТОРА |
ОБОЗНАЧЕНИЕ |
ОПРЕДЕЛЕНИЕ |
|||||||||||||||
1 |
Единичный |
I$ |
|
|
|
|
|
I$ψ = ψ |
|
|
|
|
|
|||||
2 |
Транспонированный |
|
|
^ |
|
|
|
|
|
|
^ |
|
||||||
Q^ |
ψ |
|
|
= |
|
* |
* |
|||||||||||
|
|
|
|
Qφ |
|
φ |
Q ψ |
|
||||||||||
3 |
Эрмитово сопряженный |
Q^ |
+ |
ψ |
|
|
Q^ |
φ |
|
= |
Q^ |
ψ |
|
φ |
||||
|
|
|
||||||||||||||||
4 |
Комплексно |
Q^ |
* |
^ |
|
|
* |
|
|
^* |
|
* |
|
|
|
|||
|
сопряженный |
|
|
|
|
(Q ψ) |
|
= Q |
ψ |
|
|
|
|
|||||
5 |
Самосопряженный |
Q^ |
|
ψ |
Q^ |
φ |
|
= |
Q^ ψ |
φ ; |
||||||||
(эрмитовый) |
|
|
|
|
|
|
^ |
+ |
|
|
^ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Q = Q |
|
|
|
|
|
|||||
6 |
Обратный |
Q^−1 |
Q^-1 Q^ |
= Q^ |
Q^-1 |
= I$ |
|
|||||||||||
7 |
Унитарный |
Q^ |
|
^+ |
^ |
|
|
^ |
^ |
+ |
|
$ |
|
|||||
|
Q Q = QQ |
-1 |
= I; |
|
||||||||||||||
|
|
|
|
|
|
|
|
^ |
+ |
|
|
^ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
= Q |
|
|
|
|
|
|
||
Учитывая определение скалярного произведения (определение 9), некоторые соотношения, представленные в таблице, можно также записать в развернутой, интегральной форме. В частности, операцию транспонирования (№ 2) можно представить в виде:
|
|
|
|
|
|
|
ψ Qϕ dV = |
|
|
|
|
∫ |
∫ |
ϕ Qψ dV = |
Qψ |
||
|
|
|
∫ |
||
|
|
|
|
|
|
ϕdV . (11.1)
Таким образом, транспонированный оператор просто переносит действие оператора с одной функции φ на другую – ψ . Переход к эрмитовому сопряжению (№ 3) в интегральной форме имеет вид:
∫ |
ψ |
|
|
∫ |
+ |
|
ϕdV. |
(11.2) |
|
|
|
|
|||||
|
Qϕ dV = |
|
Q |
ψ |
||||
В отличие от предыдущей процедуры, перенесение действия оператора сопровождается также внесением его под знак комплексного сопряжения.
Пример 1. Пусть имеется оператор |
|
|
d |
|
Построить транс- |
|
Q = px |
= −ih |
. |
||||
|
||||||
|
|
|
dx |
|
||
понированный (а), эрмитово сопряженный (б) и комплексно сопряженный (в) операторы.
Решение:
а) Для определенности рассмотрим ограниченную в пространстве квантовую систему с исчезающими на бесконечности волновыми функциямиϕ (±∞)=ψ (±∞)= 0 . Задачу перебрасывания действия дифференциального
23
оператора с одной функции на другую под интегралом можно осуществить,
используя процедуру интегрирования по частям:
+∞ |
|
|
|
+∞ |
|
dϕ |
|
|
+∞ |
|
+∞ |
|
dψ |
|
|
|
+∞ |
|
|
dψ |
|
|
|
+∞ |
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕdx . |
||||||||||||||
∫ |
ψ |
|
Qϕdx = −ih |
∫ |
ψ |
|
dx = −ih ψ ϕ |
|
− |
∫ |
ϕ |
|
|
dx |
|
= |
∫ |
ih |
|
|
|
ϕdx = |
∫ |
Qψ |
|
|||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
dx |
|
|
−∞ |
|
|
dx |
|
|
|
|
dx |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|||||||
−∞ |
|
|
|
−∞ |
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
−∞ |
|
|
|
|
||||
Откуда, получаем результат: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(11.3) |
|||
|
|
|
|
|
|
|
Q = ih |
|
= −Q. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
б) Вычисления в последнем примере также можно записать в виде:
+∞ |
|
|
|
+∞ |
−ih |
dψ |
|
+∞ |
|
+ |
|
∫ψ |
Qϕ dx = ∫ |
dx |
ϕdx = ∫ Q |
ψ |
ϕdx. |
||||||
−∞ |
|
|
|
−∞ |
|
|
−∞ |
|
|
|
|
Следовательно: |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
(11.4) |
|
|
|
|
|
Q |
= −ih |
= Q. |
|
|
|||
|
|
|
|
dx |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
в) В соответствие с определением № 4, получаем:
|
|
|
|
|
dψ |
|
|
|
d |
|
|
|
|
, где |
|
Qψ |
= |
−ih |
|
|
= ih |
|
ψ |
|
= Q ψ |
|
|||||
|
dx |
|
|
||||||||||||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
d |
|
|
|
|
|
|
(11.5) |
|
|
|
|
Q |
= ih |
|
= −Q. |
|
|
||||||
|
|
|
|
|
dx |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из приведенного примера можно сделать некоторые полезные выводы:
1) Операции комплексного и эрмитового сопряжения не совпадают
|
+ |
Q≠ Q .
2)Сравнивая соотношения (11.3)-(11.5), легко заметить, что операция эрмитового сопряжения можно свести к двум операциям: транспонирования
икомплексного сопряжения. Этот результат не случаен, а носит общий характер.
3) Важно также отметить, что оператор px относится к классу самосо-
пряженных (эрмитовых) операторов (опр. № 5). Этот результат также является принципиальным для квантовой механики.
Укажем фундаментальные свойства линейных самосопряженных (эрмитовых) операторов:
Теорема 1. Собственные значения эрмитовых операторов есть действительные числа.
Пусть оператор Q является эрмитовым и, для простоты, обладает дис-
кретным спектром собственных значений qn, т.е. Qψn = qnψn . Рассмотрим
среднее значение от оператора Q , которое, согласно общим правилам квантовой механики, равно:
|
|
|
|
qnψn = qn ψn |
|
(11.6) |
Q |
= ψn |
Qψn |
= ψn |
ψn . |
||
|
|
|
|
|
|
|
24

С другой стороны, на основании свойства эрмитовости, имеем:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= q ψ |
|
|
|
|
. |
(11.7) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Q |
= ψ |
n |
Qψ |
n |
= |
Qψ |
n |
ψ |
n |
= q ψ |
|
ψ |
n |
n |
|
ψ |
n |
|||
|
|
|||||||||||||||||||
|
|
|
|
|
|
n n |
|
|
n |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Сравнивая (6) и (7), окончательно получаем:
qn = qn . (11.8)
Теорема 2. Собственные функции эрмитовых операторов взаимно ортогональны.
Пусть оператор Q , как и в предыдущем случае, является эрмитовым и
обладает дискретным спектром собственных значений qn, т.е. Qψn = qnψn . Докажем, что
|
ψm |
|
ψn |
= 0 при m ≠ n. |
(11.9) |
|||
|
||||||||
Рассмотрим вначале случай, когда |
спектр собственных значений qn является |
|||||||
невырожденным. |
|
|
|
|
|
|||
Образуем скалярное произведение вида: |
|
|
||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|||
ψm |
Qψn = ψm |
|
qnψn = qn ψm |
|
ψn ; |
|||
|
|
|||||||
|
|
|
|
|
|
|
|
|
С другой стороны, учитывая свойство эрмитовости Q и результаты теоремы 1, можно записать:
|
|
|
|
|
|
|
|
|
|
|
|
|
= q ψ |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ψ |
m |
Qψ |
n |
= |
Qψ |
m |
ψ |
n |
= q ψ |
|
ψ |
n |
m |
|
ψ |
n |
= q ψ |
m |
|
ψ |
n |
||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
m m |
|
|
m |
|
|
m |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычитая из первого равенства второе, получим условие:
(qn −qm ) ψm |
|
ψn = 0. |
(11.10) |
|
|
||||
Если спектр не вырожден, то при m ≠ n , qm −qn ≠ 0 |
и выполняется условие |
|||
(11.9). |
|
|
|
|
Докажем, что теорема верна и при наличии вырождения. Рассмотрим, |
||||
например, случай двукратного вырождения, т.е. |
|
|||
|
|
(11.11) |
||
Qψ1 = qψ1; |
Qψ2 = qψ2 . |
|||
В этом случае 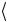 ψ1 ψ2
ψ1 ψ2 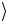 ≠ 0. Покажем, что всегда можно выбрать другую пару волновых функций φ1 и φ2 , которые физически эквивалентны первоначаль-
≠ 0. Покажем, что всегда можно выбрать другую пару волновых функций φ1 и φ2 , которые физически эквивалентны первоначаль-
ным, т.е. принадлежат тем же собственным значениям оператора Q , но будут, однако, ортогональны друг другу.
В силу линейности оператора Q , любая линейная комбинация функций
ψ1 и ψ2 является собственной функцией Q , соответствующая собственному значению q. Действительно, пусть ϕ = c1ψ1 +c2ψ2 , тогда
|
|
|
|
|
= q (c1ψ1 + c2ψ2 )= qϕ. |
Qϕ = Q (c1ψ1 |
+ c2ψ |
2 )= c1 Qψ1 |
+ c2 Qψ2 |
||
Так как с1 и с2 – произвольные числа, то выберем два варианта: а) с1 = 1; с2 = 0 (ϕ1 =ψ1 ), б) c1 = − ψ1 ψ2
ψ1 ψ2 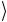 ; c2 =1 (ϕ2 = c1ψ1 +ψ2 ). Новые функции φ1 и φ2 принад25
; c2 =1 (ϕ2 = c1ψ1 +ψ2 ). Новые функции φ1 и φ2 принад25

лежат собственному значению q, однако, являются ортогональными, действительно:
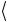 ϕ1 ϕ2
ϕ1 ϕ2 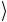 =
= ψ1 c1ψ1 +ψ2
ψ1 c1ψ1 +ψ2 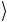 = c1
= c1 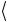 ψ1 ψ1
ψ1 ψ1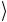 +
+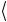 ψ1 ψ2
ψ1 ψ2 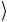 = c1 +
= c1 +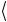 ψ1 ψ2
ψ1 ψ2 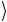 = −
= −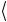 ψ1 ψ2
ψ1 ψ2 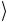 +
+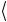 ψ1 ψ2
ψ1 ψ2 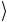 = 0.
= 0.
В случае к-кратного вырождения, аналогичным образом, всегда можно выбрать к других ортогональных линейных комбинаций первоначальных функций, принадлежащих тому же собственному значению q.
Таким образом, в дальнейшем всегда будем считать, что собственные функции любого линейного эрмитового оператора являются ортогональными.
Замечание. |
|
|
|
|
Условия |
ортогональности |
ψn ψm = 0 (n ≠ m) |
и |
нормировки |
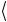 ψn ψm
ψn ψm =
=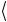 ψn ψn
ψn ψn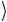 =1 (n = m) можно объединить в виде единого формального
=1 (n = m) можно объединить в виде единого формального
равенства (условие ортонормированности): |
|
|||
ψn |
|
ψm |
=δnm , |
(11.12) |
|
||||
где введен символ Кронекера: |
n ≠ m; |
|
||
|
|
0, |
(11.13) |
|
δnm = |
n = m. |
|||
|
|
1, |
|
|
Теорема 3. Совокупность всех собственных функций любого линейного эрмитового оператора образует полную систему.
Пусть ψ1,ψ2 ,... – набор всех собственных функций некоторого линейного
эрмитового оператора Q . Свойство полноты состоит в том, что произволь-
ную функцию φ всегда можно представить в виде разложения: |
|
ϕ = ∑ciψi . |
(11.14) |
i |
|
Для наглядности, можно провести аналогию с векторной алгеброй. Например, любой вектор а в трехмерном пространстве можно разложить по полной системе ортонормированных векторов (i, j,k ): a = axi + ay j + azk .
Некоторые авторы это утверждение относят к разряду одного из постулатов квантовой механики. Мы будем считать, что “обоснование” этой тео-
ремы содержится в принципе суперпозиции состояний (постулат 5).
§12. Операторы и измеряемые величины
Всвязи со статистическим характером квантовой механики, экспериментально измеряемыми параметрами являются средние значения физических величин, которые вычисляются по формуле:
|
|
(12.1) |
F = ∫ψ FψdV = ψ |
Fψ , |
где ψ – нормированная волновая функция, описывающая состояние кванто-
вой системы, а F – оператор соответствующей измеряемой величине. 26

Если ψ является собственной функцией оператора |
|
|
= λ . |
F , т.е. |
Fψ = λψ , то F |
Известно, что все измеряемые параметры прежде всего должны быть вещественными. Следовательно, операторы физических величин должны иметь толь-
ко действительные спектры собственных значений, но такими свойствами обладают только эрмитовые операторы (теорема 1). Поэтому в дальнейшем
все физические операторы будем считать эрмитовыми.
Рассмотрим общий случай, когда состояние квантовой системы описывается произвольной (нормированной) функцией φ. Учитывая свойство полноты собственных функций эрмитовых операторов ψk (теорема 3), можно
записать разложения:
ϕ = ∑ckψk ;
k |
(12.2) |
|
ϕ = ∑cnψn. |
||
|
||
n |
|
Вычислим среднее значение 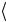 F
F по общей формуле (1), используя свойство ортонормированности функций ψk (теорема 2):
по общей формуле (1), используя свойство ортонормированности функций ψk (теорема 2):
|
|
|
|
|
|
|
|
|
|
|
= ∑∑cnckλk ψn |
|
= ∑∑cnckδnk = ∑ |
|
2 λn |
|
|
|
|
|
|
|
|
||||||||||
F = |
ϕ |
F ϕ |
= |
|
∑cnψn |
F |
|
∑ckψk |
ψk |
cn |
||||||
|
|
|
|
|
n |
|
|
|
k |
|
n k |
|
n k |
n |
|
|
|
|
|
|
|
||||||||||||
(12.3)
Из теории вероятности известно, что, если λ1,λ2 ,... – возможные значения случайной величины F, появляющиеся с вероятностями w1, w2 ,... , то
F = ∑wnλn . |
|
|
|
|
|
|
(12.4) |
n |
|
|
|
|
|
2 |
|
Сравнение формул (12.3) и (12.4) показывает, что w |
= |
|
c |
n |
|
. Отсюда |
|
|
|
||||||
n |
|
|
|
|
|
|
можно сделать общий вывод: при измерении физической величиныF для квантовой системы, находящейся в произвольном состоянии с волновой функцией
ϕ мы получим собственные значения λ1,λ2 ,... оператора F , при этом величина cn 2 равна вероятности измерения n-го собственного значения λn .
Полученные результаты носят фундаментальный характер, которые логично включить в качестве дополнительных постулатов квантовой механики:
Постулат 6. В квантовой механике каждой физической величине ставится в соответствие некоторый линейный эрмитовый оператор.
Постулат 7. При измерении физической величины F получается
спектр собственных значений соответствующего оператора F .
До сих пор обсуждался вопрос об измерении одной физической величины. Рассмотрим теперь проблему измерения сразу нескольких величин. Ранее мы видели, что в микромире имеются случаи принципиальной невозможности одновременного измерения нескольких физических величин (соотноше-
ния неопределенности Гейзенберга).
27
С теоретической точки зрения можно поставить вопрос о разработке критериев возможности решения указанной проблемы на языке операторов.
Так как измеряются собственные значения операторов, то этот критерий сво-
дится к выяснению вопроса о том, когда два оператора F и R имеют общие
собственные функции. Поставленная задача решается в общем виде с помощью следующих трех теорем (доказательство приведено в задачах к главе 2).
|
|
|
|
|
Теорема 1. Если операторы F |
и R имеют общие собственные функ- |
|||
|
|
|
|
|
ции, то такие операторы между собой коммутируют: F, R = 0. |
||||
|
|
|
|
|
|
коммутируют, то они |
|||
Теорема 2 (обратная). Если операторы F |
и R |
|||
имеют общие собственные функции.
Теорема 3. Пусть имеется две физические величины F и R , самосопряженные операторы которых не коммутируют, так что выполняется условие:
|
|
|
|
F, R |
= i K . |
||
|
|
|
|
Тогда утверждается, что неопределенности измерения величин связаны условием:
F R ≥ 1 |
K |
|
|
2 |
|
F и R
(12.5)
Доказательство этих теорем приведено в задачах (2.7) - (2.9).
Пример. Известно, что между операторами координаты и импульса
|
|
|
= 0; |
|
|
|
= ih. Тогда на |
существуют коммутационные условия вида: x$ |
, p y |
x$ |
, px |
||||
|
|
|
|
|
|
|
|
основании указанных теорем, можно утверждать о возможности одновременного измерения проекций x, py и справедливости соотношения неопределенности Гейзенберга:
x px |
≥ |
h |
. |
(12.6) |
|
||||
|
2 |
|
|
|
В квантовой механике существует альтернативный способ определения действия оператора на волновую функцию в виде умножения матриц, так на-
зываемая матричная квантовая механика (Гейзенберг). Рассмотрим вначале основные понятия матричного исчисления.
§ 13. Алгебра матриц
Определение 1. Матрицей порядка m ×n называется математический объект, представляющий собой множество m ×n , вообще говоря, комплексных чисел, расположенных в прямоугольной таблице из m строк и n столбцов.
28
Матрицы записываются в виде символов
a11
A = (a jk )= a21am1
a12 ... |
a1n |
|
||
a ... |
a |
. |
(13.1) |
|
22 |
|
|
2n |
|
a |
... |
a |
|
|
m2 |
|
mn |
|
|
Первый индекс МЭ указывает номер строки, второй – номер столбца. В квантовой механике чаще всего имеют дело с матрицами трех типов:
1. Квадратные матрицы порядка n ×n ;
2. |
Матрица-столбец порядка m ×1 : |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
ψ1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( j1 ) |
= |
( |
j |
) |
= |
ψ2 |
|
; |
(13.2) |
|||
|
|
|
|
|||||||||||
|
|
ψ = |
ψ |
ψ |
|
... |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
ψ |
|
|
|
|
|
3. |
Матрица-строка порядка 1×n : |
|
|
|
|
|
m |
|
|
|
||||
j ) |
|
|
|
|
|
|
n ) |
|
|
|||||
|
|
( 1 j ) |
( |
|
( |
1 2 |
|
; |
(13.3) |
|||||
|
|
ψ = ψ |
= ψ |
|
= |
ψ ψ |
|
...ψ |
|
|
||||
|
Понятие матрицы становится содержательным лишь тогда, когда над |
|||||||||||||
этими объектами введены основные алгебраические операции. |
|
|||||||||||||
|
Определение 2. Матрицы называются равными, если их |
порядок оди- |
||||||||||||
наков и равны между собой соответствующие м.э. (A = B a jk = bjk ) . |
||||||||||||||
|
Определение 3. Суммой матриц A и B называется матрица C = A + B , |
|||||||||||||
если все три матрицы имеют одинаковый порядок и c jk = a jk +bjk . |
|
|||||||||||||
|
Определение 4. Произведением матрицы A на число α называется мат- |
|||||||||||||
рица B =α A того же порядка, что и A , а М.Э: |
|
|
|
|
||||||||||
|
|
|
bjk |
=αajk . |
|
|
|
|
|
(13.4) |
||||
|
Определение 5. Произведением матрицы A порядка m ×n на матрицу B |
|||||||||||||
порядка n ×l |
называется такая матрица C = AB |
порядка m ×l , у которой м.э. с |
||||||||||||
индексом i и |
j равен сумме произведения всех элементов i -ой строки матри- |
|||||||||||||
цы A на соответствующие элементы j -го столбца матрицы B : |
|
|||||||||||||
|
|
|
n |
|
|
|
|
где i =1, 2,3,...m . |
|
|||||
|
|
cij = ∑aikbkj , |
|
(13.5) |
||||||||||
|
|
|
k =1 |
|
|
|
|
|
|
j =1, 2,3,...l |
|
|||
Очевидно, что произведение матриц определено лишь в том случае, ес-
ли число столбцов матрицы A равно числу строк матрицы B. В частности,
при умножении двух квадратных матриц порядка n×n получится квадратная матрица того же порядка. Важно отметить, что матрицы образует алгебру не-
коммутируемых величин.
29

Пример 1. При умножении квадратной матрицы порядка n ×n на столбец порядка n ×1 получается матрица-столбец порядка n ×1:
×=
Следует сразу заметить, что обратное произведение столбца на квадратную матрицу не определено:
× |
|
– не определено |
|
|
|
Этот результат еще раз подтверждает некоммутативность произведе-
ния матриц.
Произведение матрицы-строки на квадратную матрицу дает матрицустроку:
× =
Однако, обратное произведение также не определенно:
× |
|
– не определено |
|
Умножение матрицы-строки порядка 1×n на матрицу-столбец порядка n ×1 дает квадратную матрицу порядка 1×1, т.е. число:
× =
Обратное произведение – не определено:
××  – не определено
– не определено
Определение 6. Следом (шпуром) квадратной матрицы порядка n ×n
называется сумма его диагональных элементов:
n |
|
SpA = ∑aii |
(13.6) |
i=1
30
