
с.м.чернов_квантовая механика
.pdf
ЗАДАЧИ С РЕШЕНИЯМИ
Задачи к главе I
1.1. Показать, что в теории Планка средняя энергия радиационных осцилляторов определяется формулой (1.9). Считать, что вероятность распределения осцилляторов по энергиям описывается законом Больц-
мана wn |
|
E |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
= c exp - |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
kT |
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
В теории Планка En = nhω . Тогда |
|
|
|
|
|
hω |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
∞ |
|
∞ |
|
|
|
|
|
|
∞ |
|
|
||||||||||||||
|
|
|
|
|
∑Enwn |
|
∑nhωc exp −n |
|
|
|
|
|
∑ne−nx |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
ε |
= |
n=0 |
|
= |
n=0 |
|
|
|
|
|
kT |
= hω |
n=0 |
= |
|
||||||||||||||
|
|
∞ |
∞ |
|
|
|
hω |
∞ |
||||||||||||||||||||||
|
|
|
|
|
|
∑wn |
|
∑c exp |
−n |
|
|
∑e−nx |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
n=0 |
|
n=0 |
|
|
|
kT |
|
|
n=0 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||
|
= −hω d ln ∑e−nx = −hω d ln |
|
|
|
= hω = hω |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
n=0 |
|
|
|
dx |
|
1−e−x |
|
|
ex −1 |
|
|
hω |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
e kT |
−1 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
hω |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где было введено обозначение x ≡ |
|
|
и использована формула для суммы |
|||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
kT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
бесконечно убывающей геометрической прогрессии.
1.2. Вычислите сдвиг длины волны света, рассеянного на покоящихся электронах (эффект Комптона).
Решение:
Запишем законы сохранения энергии и импульса для системы: фотон и
электрон: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
= hω |
+ mc |
; |
|
|
|||||
|
|
|
|
hω0 + m0c |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
hk0 = hk + mv. |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
ω) |
+ m0c |
|
= mc |
|
; |
|
|
||||||
|
|
|
|
h(ω0 − |
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
|
|
h(k |
0 |
−k)= mv. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Возведем последние равенства в квадрат: |
|
|
|
|
|
|
|
|
|||||||||||||
|
h2ω02 − 2h2ω0ω + h2ω2 + m02c4 + 2hm0c2 (ω0 −ω)= m2c4 ; |
(1) |
|||||||||||||||||||
2 |
2 |
2 |
k0k cosθ |
2 |
k |
2 |
|
|
|
|
2 |
2 |
; |
|
|
учтем, чтоk = |
ω |
||||
h |
ko |
− 2h |
+ h |
|
= m |
v |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
h2ω2 |
− 2h2ω ωcosθ + h2ω2 |
= m2v2c2 . |
|
(2) |
||||||||||||||
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычтем из (1) уравнение (2):
142

|
2 |
|
|
|
|
|
|
2 |
4 |
|
|
|
|
|
2 |
c |
2 |
(ω0 |
−ω) |
|
2 |
c |
4 |
|
− |
v2 |
2 |
4 |
, |
|||||||||
|
−2h |
ω0ω(1 |
− cosθ )+ mo c |
|
|
+ 2h |
|
= m |
|
1 |
c |
2 |
|
= m0 c |
|
|||||||||||||||||||||||
|
m0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где m = |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 − |
|
v2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
hω0ω |
|
|
|
|
|
|
|
|
|
|
|
= 2hω0ω sin2 θ |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
ω |
−ω = |
|
(1 −cosθ ) |
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
0 |
|
m c2 |
|
|
|
|
|
|
|
|
|
|
|
|
m c2 |
|
|
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
= |
|
|
2πc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Переходя к длинам волн ω |
|
|
|
|
|
|
|
|
|
, получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
λ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
2h ( |
2πc)2 |
|
2 |
θ |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2πc |
|
|
|
|
− |
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
sin |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
λ |
|
|
λ |
|
|
|
m c |
2 |
|
λ λ |
|
2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отсюда приходим к формуле Комптона: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
λ =λ −λ |
|
= 4πhsin2 θ = 2Λsin2 θ , |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
m0c |
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где
Λ = 2πh = 2,42 10−12 м – комптоновская длина волны электрона. m0c
Ответ: 2Λsin2 θ2 .
1.3. Найти направление вылета электрона отдачи по отношению к направлению движения налетающего рентгеновского фотона частоты ω0 , рассеиваемого на покоящихся электронах под углом θ.
|
|
Решение: |
Ро |
|
Р |
|
ϑ |
|
|
|
ϕ |
|
|
|
|
|
Ре |
По закону сохранения импульса P0 = P + Pe , или в проекциях:
Ox : |
P0 = Pcosθ + Pe cosϕ; |
|
|
|
Oy : |
Psinθ = P sinϕ; |
P = P |
sinθ |
. |
|
||||
|
e |
e |
sinϕ |
|
|
|
|
||
P0 = P cosθ + Psinθ ctgϕ .
143

|
|
|
|
|
|
|
|
|
|
|
|
|
P0 |
|
−cosθ |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
ctgϕ = |
|
P |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
sinθ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
С другой стороны P = hk = |
|
2πh |
|
|
и |
|
P0 |
= |
|
λ |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
λ |
|
|
|
|
|
|
P |
|
|
λ0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
Из формулы Комптона находим |
|
|
λ |
=1 + 2 |
|
Λ |
sin2 θ . |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
λ0 |
|
|
|
|
|
|
|
λ0 |
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
θ |
|
|
|
|
|
|
θ |
|
|
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
θ |
|
|
|
2sin2 |
+ |
2Λsin2 |
|
θ |
|
|
hω0 |
|
||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
2 |
|
|
|||||||||||||||||||||
ctgϕ = |
|
|
1 − cosθ |
+ 2Λsin |
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= tg |
|
1 |
+ |
|
|
. |
||||||
sin |
|
|
|
|
|
|
|
|
|
|
|
θ |
|
|
θ |
|
2 |
m0c |
2 |
|||||||||||||||||
|
θ |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2sin |
|
|
|
|
|
|
|
|
||||||||||||
Ответ: ctgϕ = tg θ |
|
|
hω0 |
|
|
|
|
|
|
|
|
|
2 cos 2 |
|
|
|
|
|
|
|
|
|||||||||||||||
1+ |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
2 |
|
|
m c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1.4. Согласно теории Планка, осуществляются лишь такие состояния линейного гармонического осциллятора, энергия которого равна
E = |
p2 |
+ |
mω2 x2 |
= nhω, n = 0,1, 2, ... |
|
x |
|
||||
2m |
2 |
||||
|
|
|
Показать, что фазовая траектория осциллятора представляет собой эллипс с дискретной площадью.
Примечание: Фазовой плоскостью называется плоскость с осями
(x, px ).
Решение:
Из формулы Планка легко получить на фазовой плоскости каноническое уравнение эллипса:
x2 |
+ |
p |
x |
2 |
=1 |
|
a 2 |
b2 |
|||||
|
|
|||||
с полуосями a = |
2πh |
, b = 2mnhω. |
|
mω |
|||
|
|
Площадь эллипса равна:
S =ο∫pxdx =πab =2πh n, n =0,1,2,...
В последнем соотношении отсутствует какая-либо информация об особенностях осциллятора (m,ω). Поэтому естественно предположить, что такое
условие квантования справедливо и для любой механической системы. В общем случае состояние механической системы с k степенями свободы описывается k обобщенными координатами (q1, q2 ,..., qk ) и обобщенными импуль-
сами (p1, p2 ,..., pk ), которые должны быть связаны k условиями квантования:
144
ο∫ pidqi = 2πh ni
где i =1, 2,..., k; ni = 0,1, 2,..., а интегрирование ведется вдоль замкнутой тра-
ектории на фазовой плоскости. Полученные соотношения называются усло-
виями квантования Бора-Зоммерфельда. Заметим, что количество квантован-
ных чисел ni равно числу степеней свободы k .
1.5. Показать, что в атоме водорода возможны лишь такие круговые орбиты электрона, для которых момент импульса L = mvr = nh
(n = 1,2,3,…).
Решение:
В качестве обобщенной координаты удобно взять азимутальный угол q =ϕ (0 ≤ϕ ≤ 2π ). Для вращательного движения роль линейной скорости
v играет угловая скорость ω (v =ωr), а роль массы – момент инерции
I = mr2 . Следовательно, обобщенный импульс электрона равен
p0 = Iω = mr2ω = mvr = L .
Таким образом, при вращательном движении обобщенный импульс равен моменту импульса. При равномерном вращении электрона по круговой орбите L = const , и на основании условия квантования Бора-Земмерфельда имеем:
2π
ο∫ p0dq = ο∫ Ldϕ = L ∫ dϕ = L 2π = 2πh n
0
и, следовательно L = nh (n = 0,1, 2,...).
Следует, однако, отметить, что случай n = 0 следует исключить как не имеющий физического смысла. Почему?
1.6. Используя условие квантования Бора-Зоммерфельда, найти возможные значения энергии E частицы массы m, движущейся в одномерной потенциальной яме U(x) ширины ac бесконечно высокими стенками:
|
|
|
0, 0 ≤ x ≤ a |
. |
|
|
U(x)= |
|
|
|
|
∞, x ≤ 0, x ≥ a |
|
|
|
|
Решение: |
|
|
|
|
|
|
& |
Обобщенные координаты и импульс равны: q = x, p0 = px = mx |
||||
Частица может двигаться лишь внутри ямы с постоянным по модулю |
||||
импульсом |
px |
= const. Тогда на |
основании условия квантования Бора- |
|
Зоммерфельда имеем очевидную цепочку равенств: |
||||
|
|
a |
a |
|
|
|
ο∫ pdq = 2∫ px dx = 2 px ∫dx = 2 pxa = 2πhn. |
||
0 |
0 |
|
||
|
|
|
145 |
|
Отсюда находим условия квантования импульса и энергии
p |
x |
= |
|
πhn |
; |
|
|
|
||||
|
a |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
p2 |
|
|
π2h2 |
|
|
|
||
E = |
|
|
x |
|
= |
|
|
n2 |
, |
n = 0,1,2,... |
||
2m |
|
2ma2 |
||||||||||
|
|
|
|
|
|
|
|
|||||
Следует отметить, что последний результат совпадает со строгим кван- тово-механическим расчетом (за исключения случая n = 0).
1.7. Показать, что частота излучения водородоподобного атома, соответствующего переходу электрона с (n + 1)-ой орбиты на n-ю, равна
частоте обращения на n -й орбите, лишь если n.1 (принцип соответствия Бора).
Решение:
|
|
В соответствии с формулой |
ω |
|
|
|
= RZ |
2 |
1 |
|
|
− |
1 |
|
|
|
частота излучения ато- |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
n |
2 |
|
|||||||||||||||||||||||||||||||||||||||||||
ма водорода равна: |
|
|
|
|
|
|
|
|
|
|
|
kn |
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2n +1) |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
RZ |
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ω = |
RZ 2 |
|
− |
|
|
|
|
|
|
= |
|
|
. |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
(n + |
1) |
|
|
|
|
|
n |
(n + |
1) |
2 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Частоту обращения электрона на п-й круговой орбите ω0 |
найдем из ус- |
|||||||||||||||||||||||||||||||||||||||||||||||||||
ловия |
|
mv2 |
= |
|
|
Ze2 |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
r |
|
|
4πε0r2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mv2 = mω2r = |
|
|
Ze2 |
|
ω = |
|
|
|
|
Ze2 |
. |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4πε0r2 |
|
4πε0mr3 |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
Подставляя |
в |
последнюю |
формулу |
радиус |
|
п-й боровской орбиты |
||||||||||||||||||||||||||||||||||||||||||||||
|
a |
|
|
2 |
|
|
|
|
|
4πε |
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
me2 |
|
|
|
|||
r = |
0 |
|
n |
, a |
= |
|
0 |
|
|
и вводя постоянную Ридберга |
R = |
|
|
|
|
|
, имеем: |
|||||||||||||||||||||||||||||||||||||
n |
Z |
|
|
0 |
|
|
me2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2h3 (4πε |
0 )2 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω = |
|
2RZ 2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2n +1)n3 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Для отношения |
|
ω |
|
|
окончательно получаем: |
|
ω |
|
= |
|
. |
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
ω0 |
|
|
|
ω0 |
|
|
2n2 |
(n +1)2 |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
При переходе с первого возбужденного уровня на основной уровень |
||||||||||||||||||||||||||||||||||||||||||||||||||||
атома |
|
|
водорода(n =1) |
|
|
ω |
= |
3 |
. Однако, |
|
при |
|
|
высоких |
квантовых числах |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
8 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
ω |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
n → ∞, |
|
→1 , |
т.е. результат для квантовой системы совпадает с классиче- |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
ω |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
146 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ским, (принцип соответствия Бора). Данный результат имеет общий характер и выполняется для всех квантовых систем.
1.8. Оценить с помощью соотношений неопределенности Гейзенберга “размеры” и энергию основного состояния атома водорода и гелия.
Решение:
Для оценок параметров этой задачи будем считать, что электроны атома движутся внутри сферы радиуса r с импульсом p , связанным соотношением
неопределенности:
r p h. |
(1) |
(Для атомов конечных размеров, p p и r |
r , так как средние значе- |
ния  p
p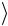 = 0,
= 0, 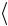 r
r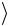 = 0 ). Полная энергия атома водорода (для неподвижного, точечного ядра) равна:
= 0 ). Полная энергия атома водорода (для неподвижного, точечного ядра) равна:
E = E |
k |
+ E |
n |
= |
|
p2 |
|
− |
|
e2 |
(2) |
|||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
2m 4πε0r |
|
|||||||||||
или с учетом (1): |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
h2 |
|
|
|
|
|
|
e2 |
|
|
|
|
|
||
E = |
|
|
|
− |
|
|
|
|
|
. |
|
(3) |
||||||
|
2mr2 |
|
4πε |
0r |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Минимизируя энергию атома по r , находим искомые параметры |
|
|||||||||||||||||
r = a |
|
= 4πε0h |
2 |
= 0,528 A; |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
|
|||
min |
|
0 |
|
|
|
me4 |
|
|
|
|
|
|
|
|
(4) |
|||
E0 = − |
|
|
|
me4 |
|
|
|
|
= −13,6эВ. |
|||||||||
2h2 (4πε0 )2 |
|
|
||||||||||||||||
Следует отметить, что оценки “размеров” и энергии основного состояния атома водорода (4) совпадают с результатом теории Бора и точными квантовомеханическими расчетами, хотя это совпадение следует считать случайным.
Для атома гелия, предполагая, что в среднем электроны располагаются на противоположных концах диаметра, имеем:
E = 2 |
p2 |
− 2 |
2e2 |
+ |
e2 |
= |
p2 |
− |
7 e2 |
|
h2 |
− |
7 e2 |
. (5) |
||
|
|
|
|
|
|
|
|
|
||||||||
2m |
(4πε0 )r |
(4πε0 )2r |
|
2 (4πε0 )r |
2mr 2 |
2 (4πε0 )r |
||||||||||
|
|
|
|
m |
|
|
|
|||||||||
Найдя минимум функции (5), для атома гелия получаем:
|
|
4 4πε |
0 h |
2 |
|
4 a |
|
o |
|
r |
= |
|
= |
|
= 0,30 A |
||||
|
|
|
|
|
|||||
7 me2 |
|
|
|||||||
min |
|
|
|
7 |
0 |
|
|||
E |
= − |
49 |
|
me4 |
|
= −79 |
эВ. |
(6) |
|
|
(4πε |
0 )2 |
|||||
0 |
|
16 h2 |
|
|
|
|||
Уменьшение “размеров” атома гелия по сравнению с атомом водорода объясняется увеличением заряда ядра атома вдвое.
147

Для сравнения приведем экспериментальное значение энергии основного состояния гелия:
Еэксп = −83 эВ.
Таким образом, соотношения неопределенности позволяют сделать оценки атомных параметров с относительно хорошей точностью.
1.9. Ядра атомов состоят из протонов и нейтронов. Почему в ядре не может находиться электрон или другая “легкая” частица?
Решение:
Укажем вначале характерные пространственные и энергетические масштабы ядерной физики, полученные экспериментально.
“Размер” ядра: ro ≈ 10-14 м, удельная энергия связи:
E0 = EAсв 8,6 МэВ ≈1, 4 10−12 Дж.
Качественно на поставленный вопрос можно ответить, сравнивая кинетическую энергию элементарной частицы массы m , движущейся в области r0 , с удельной энергией связи E0 . Критерием устойчивости ядра может слу-
жить неравенство:
Ek ≤ E0 . |
(1) |
Оценим Ek , используя соотношение неопределенности |
|
r p h; E = |
p2 |
|
h2 |
|
|
0,5 10−40 |
(Дж). |
|
2m |
2mr2 |
m |
||||||
|
|
|
|
|||||
|
|
|
0 |
|
|
|
|
|
Для электронов (m = me = 9,11 10−31 кг) |
Еке = 50 10−12 Дж. |
|||||||
Для протонов (m = mp =1,67 10−27 кг) |
|
Екр = 0,03 10−12 Дж. |
||||||
Сравнивая проведенные оценки с критерием (1), мы видим, что в состав ядра могут входить лишь тяжелые частицы типа p, n (нуклоны).
Известно, что в природе существуют частицы – гипероны, массы которых превышают массу нуклонов. Поэтому следует ожидать наличие в природе ядер, содержащих кроме нуклонов также и гипероны (гиперядра). В настоящее время обнаружены экспериментально более двух десятков одиночных и двойных Λ-гиперядер, а также ∑-гиперядра.
1.10. Группа волн имеет эффективную ширину x и перемещается с групповой скоростью vx . Показать, что время прохождения волнового
пакета через некоторую точку пространства t и неопределенность кинетической энергии частицы E связаны соотношением t E h.
148
|
|
2.5. Доказать, что, если |
|
– эрмитовый оператор, |
то операторы |
|||||||
|
|
A |
||||||||||
|
|
|
+ |
|
+ |
|
|
|
|
|
|
|
B = Q AQ |
и C = Q AQ также являются эрмитовыми. |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.6. Операторы A, B и C, удовлетворяющие коммутационному ус- |
||||||||||
ловию |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
[A,B] = C, преобразуются в штрихованные операторы согласно условию |
||||||||||||
|
|
+ |
|
|
|
|
|
+ |
= I$). Доказать, что новые |
|||
A′ = Q AQ |
, где Q – унитарный оператор (QQ |
|||||||||||
операторы удовлетворяют тому же коммутационному условию. |
|
|
||||||||||
|
|
2.7. Доказать, что, |
|
|
|
|
|
|
|
|||
|
|
если операторы F и |
R имеют общие собствен- |
|||||||||
ные функции, то такие операторы между собой коммутируют: |
|
|
||||||||||
[F, R] = 0. |
||||||||||||
|
|
|
|
|
|
|
Решение: |
|
|
|
|
|
|
|
Пусть |
ψ – |
общая |
собственная функция |
операторов |
|
и |
|
|||
|
|
F |
R , т.е. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Fψ = λψ, Rψ = μψ . Тогда |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[F, R]ψ = (F R− R F)ψ = λμψ − μλψ = 0. |
|
|
|
||||
|
|
Такое же равенство имеет место и для произвольной функции φ, если |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
учесть свойство полноты (11.14) и линейность операторов F и R . |
|
|
||||||||||
|
|
2.8. |
|
|
|
|
|
|
|
|
|
то они |
|
|
Доказать, что если операторы F и |
R коммутируют, |
|||||||||
имеют общие собственные функции.
Решение:
Не умаляя общности, ограничимся случаем невырожденных собствен-
|
|
|
=λψ) и |
|
|
ных значений. Пусть ψ – с.ф. оператора F |
(Fψ |
F R = R F , необходи- |
|||
|
|
|
|
|
|
мо доказать, что Rψ = μψ. |
|
|
|
|
|
Рассмотрим цепочку очевидных соотношений: |
|
|
|||
|
|
|
|
|
|
F (Rψ ) = R(Fψ ) = λ(Rψ ). |
|
|
|||
|
|
|
являются с.ф. оператора |
|
|
Отсюда следует, что функции ψ и ϕ = Rψ |
F , |
||||
соответствующие одному и тому же с.з. λ, т.е. они являются физически эквивалентными и могут отличаться лишь на произвольное число μ, т.е.
Rψ = μψ.
150

 отмечена функция, на которую действует оператор дифференцирования
отмечена функция, на которую действует оператор дифференцирования