
с.м.чернов_квантовая механика
.pdfВ нулевом приближении U (r) = 0 , и уравнение Шредингера примет вид:
(Δ+k02)ψ(0) =0, |
(44.3) |
|||||
решение которого известно: ψ(0) =eik0 r |
|
|
|
|
|
|
. |
|
|
|
|
|
|
В первом приближении: |
2m |
|
|
|
||
(Δ+k02)(ψ(0) +ψ(1) ) = |
U(r)(ψ(0) +ψ(1) ) . |
(44.4) |
||||
2 |
||||||
|
|
h |
|
|||
Отбрасывая справа квадратичный член по возмущению |
( u(r) ψ (1) ) и, |
|||||
учитывая уравнение (44.3), для ψ (1) получаем уравнение: |
|
|||||
ψ(1) +k02ψ(1) = |
|
2m |
U(r)ψ(0) . |
(44.5) |
||
|
2 |
|||||
|
|
h |
|
|||
Замечание. Рассмотрим решение уравнения (44.5), которое было получено в электродинамике.
В электродинамике электрическое поле можно описать скалярным потенциалом ϕ(r, t) , который создается электрическими зарядами с плотностью ρ(r, t) . Причем, из уравнения Максвелла получено уравнение,
связывающее ρ с ϕ (волновое уравнение или уравнение Даламбера):
|
|
|
|
ϕ − |
1 ∂2ϕ |
= − |
|
ρ |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
∂t2 |
|
. |
|
|
|
(44.6) |
|||||||||||||
|
|
|
|
c2 |
ε0 |
|
|||||||||||||||||||||
Решением этого уравнения является так называемый запаздывающий |
|||||||||||||||||||||||||||
потенциал: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
ρ(r' ,t − |
) |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
ϕ(r,t) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
dV' . |
|
(44.7) |
|||||||
|
|
|
4πε0 |
∫ |
|
R |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Рассмотрим случай, когда ρ(r, t) |
– гармонически зависит от времени: |
|
|||||||||||||||||||||||||
|
|
|
|
ρ(r, t) = ρ0 (r)e−iωt |
|
|
|
|
(44.8) |
||||||||||||||||||
В этом случае и потенциал |
ϕ(r, t) |
|
|
также |
гармонически зависит |
от t. |
|||||||||||||||||||||
Действительно: |
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
−iω(t− |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ϕ(r, t) = |
1 |
∫ |
ρ0 (r' )e |
|
|
|
|
c |
) |
dV |
' |
= e |
−iωt |
ϕ0 (r) , |
где |
(44.9) |
|||||||||||
4πε0 |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
ϕ0 (r) = |
1 |
|
|
∫ |
|
ρ |
(r' )e−ik0R ) |
|
dV ' ; k0 |
ω |
|
||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
= c . |
(44.10) |
|||||||||||||
|
|
4πε0 |
|
|
|
|
|
|
R |
|
|
||||||||||||||||
Подставляя (44.8) и (44.9) в уравнении Даламбера (44.6), для координатных частей ρ0 (r) и ϕ0 (r) получаем уравнение:
121

|
|
|
|
|
|
|
|
|
2 |
|
ρ0 |
|
|
|||
|
|
|
|
|
ϕ0 |
(r) +k0 ϕ0 (r) = − |
|
|
|
, |
(44.11) |
|||||
|
|
|
|
ε |
0 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
решением которого является функция (44.10). |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||
Однако уравнение (44.11) по форме совпадает со стационарным УШ |
||||||||||||||||
(44.5) путем замены ϕ0 ψ (1) ; |
|
|
|
|
|
|
|
|
|
|
||||||
ρ0 − |
2mε |
0 |
U (r)ψ |
(0) |
= − |
|
2mε0 |
U (r)e |
ik r |
(44.12) |
||||||
h2 |
|
|
|
h2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Следовательно, для линейной поправки ψ (1) имеем: |
|
|
|
|||||||||||||
ψ(1) (r) =− |
m |
∫ |
1 |
U(r' )eik0 r+ik0RdV' , |
|
(44.13) |
||||||||||
2πh2 |
R |
|
||||||||||||||
где интеграл берется по области действия потенциала r' ≤ a . |
|
|||||||||||||||
Найдем асимптотическое поведение функции (44.13) при больших т.е. на расстояниях, много больших размеров области действия сил. Запишем
приближенно выражение |
R = |
|
r −r' |
|
|
. В (44.13) знаменатель заменим на R ≈ r , а |
|||||||
|
|
|
|||||||||||
в показателе экспоненты учтем следующее разложение: |
|||||||||||||
2 |
' 2 |
|
2 |
' |
|
'2 |
2 |
|
r r' |
||||
R = |
(r−r ) |
=r |
|
|
−2r r |
+r |
|
≈r |
(1−2 |
|
) |
||
|
|
|
r2 |
||||||||||
R ≈r(1−rr2r' ) .
Так как рассеянные волны распространяются по радиальным направлениям и волновой вектор k || r . то можно записать:
|
|
|
|
|
|
|
|
|
r |
= k |
|
|
|
|
|
|
|
|
|
|
|
|||
и следовательно |
|
|
|
|
|
|
|
|
r |
|
k |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k r' |
|
|
|
k r' |
|
|
|
|
||||||
|
|
|
|
|
R ≈r − |
|
|
|
= r − |
|
|
|
|
|
|
|
|
|||||||
|
|
|
k |
|
|
k0 |
|
|
|
|
|
(44.14) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(т.к. при упр. рассеянии k = k0 ). Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
(1) |
|
|
|
m |
1 |
|
' |
|
ik r' |
|
ik r −ik r |
' |
|
|
|||||||||
ψ |
|
≈− |
|
|
|
|
∫ |
|
U(r |
)e |
0 |
|
e |
0 |
e |
0 dV |
|
= |
|
|||||
|
2πh2 |
r |
|
|
|
|||||||||||||||||||
|
|
m 1 ik r |
|
|
|
' |
|
i(k |
−k) r' |
|
|
' |
|
. |
(44.15) |
|||||||||
=− |
|
|
|
e 0 |
∫U(r |
)e |
0 |
|
|
|
|
dV |
|
|
|
|
||||||||
2πh2 |
r |
|
|
|
|
|
|
|
|
|||||||||||||||
Для удобства введем, так называемый, вектор столкновения q = k0 −k . |
||||||||||||||||||||||||
Смысл его состоит в следующем: hq = hk0 −hk |
– |
вектор передачи импульса |
||||||||||||||||||||||
при рассеянии. Найдем модуль этого вектора для случая упругого рассеяния
( k = k0 ):
q2 =(k0 −k)2 =k02 +k2 −2k0k cosθ =2k02 (1−cosθ) =4k02 sin2 θ2
122

т.е. |
q =2k0 sin |
θ |
, где θ – угол рассеяния. |
|
|
(44.16) |
|||||||
|
|
2 |
|
|
|
|
|
|
|
eik0r |
|
||
|
|
|
(1) |
|
m |
' |
iq r |
' |
|
|
|||
Тогда: |
ψ |
|
|
=[− |
|
∫U(r )e |
dV |
] |
|
. |
(44.17) |
||
|
|
2πh2 |
r |
||||||||||
Сравнивая (44.17) с необходимой асимптотикой вида (44.8), окончательно для амплитуды рассеяния в первом борновском приближении получаем:
A(θ,ϕ) = − |
m |
∫U(r' )eiq rdV ' . |
(44.18) |
2πh2 |
Рассмотрим важный для практических приложений случай, когда взаимодействие U (r' ) =U (r' ) обладает свойством центральной симметрии. В этом случае, амплитуда рассеяния не зависит от ϕ , а только от угла рассеяния θ , который можно отсчитывать от направления вектора qr'
dV' =2πsinθdϑr'2dr'2
A(θ,ϕ) = − |
m |
∞∫U (r' )r'2 dr ' |
π∫eiqr' cosθ sin θdθ ; |
h2 |
|||
|
|
0 |
0 |
Вычислим внутренний интеграл:
J = π∫eiqr ' cosθ sin θ dθ = {− cos θ ≡ x} = ∫1 |
eiqr 'x dx = |
||||||
|
0 |
|
|
−1 |
|
|
|
= |
1 |
(eiqr ' − e−iqr ' ) = |
1 |
2i sin qr ' = 2 |
sin qr ' |
|
|
iqr ' |
iqr ' |
|
|||||
|
|
|
|
qr ' |
|||
A(θ) =−h22mq ∞∫U(r' )sin qr'r'dr' (символ штрих можно опустить).
0
Таким образом, в первом борновском приближении при рассеянии частицы массы m в центрально-симметричном поле U(r) дифференциальное сечение рассеяния равно:
|
|
|
|
|
|
dσ |
|
|
2 |
∞ |
|
|
|
|
|
|
|
|
|
= |
4m |
| ∫U(r)sin qrrdr |2 |
(44.19) |
||||
|
|
|
|
|
|
dΩ |
4 2 |
||||||
|
|
|
|
|
|
|
h q |
0 |
|
|
|||
где |
q =2k0 sin |
θ |
, |
k02 = |
2mE |
, |
q2 = 8mE2 |
sin2 θ . |
|
||||
2 |
2 |
|
|||||||||||
|
|
|
|
h |
|
|
h |
2 |
|
||||
123
ГЛАВА VII
Релятивистская теория частиц со спином 0 и 12
§45. Элементы специальной теории относительности (СТО)
Воснове СТО (Эйнштейн, 1905) лежат два основных постулата, подтвержденные многочисленными опытными данными:
1)Все физические явления происходят одинаково в любых инерциальных системах отсчета (ИСО). Это означает, что уравнения, описывающие эти явления, должны быть неизменными (инвариантными) при переходе от одной ИСО к любой другой ИСО.
2)В природе существует максимально предельная скорость перемещения материальных объектов, численно равная скорости света в вакууме
с=3 108 мс.
Из указанных постулатов вытекает важный закон, утверждающий, что
пространственные и временные переменные не являются независимыми, но преобразуются друг через друга при переходе от одной ИСО к другой.
z |
z′ |
|
v |
K |
K′ x, x′ |
y |
y′ |
В частности, координаты и время при переходе от неподвижной СО (К) к другой ИСО (К′), которая равномерно перемещается относительно К со ско-
ростью v вдоль направления x , связаны уравнениями:
|
|
x |
−vt |
|
|
|
|
|
|
|
|
|
|
t − |
v |
x |
|
|
||
′ |
|
|
y |
′ |
= y; |
z |
′ |
= z; |
t |
′ |
|
c2 |
|
|||||||
= |
|
|
|
; |
= |
|
|
|
. |
(45.1) |
||||||||||
x |
|
|
v2 |
|
|
|
|
|
|
|||||||||||
|
|
1− |
|
|
|
|
|
|
|
|
|
|
1− |
v2 |
|
|||||
|
|
c2 |
|
|
|
|
|
|
|
|
|
|
c2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Преобразования (45.1) называются преобразованиями Лоренца, и в случае малых скоростей переходят в преобразования Галилея:
′ |
= x − vt; |
y |
′ |
= y; |
z |
′ |
= z; |
t |
′ |
= t. |
(45.2) |
x |
|
|
|
Из преобразований Лоренца следуют парадоксальные (с точки зрения классической физики) результаты:
1) Расстояния между двумя пространственными точками, измеренные в один и тот же момент времени, связаны условием:
124
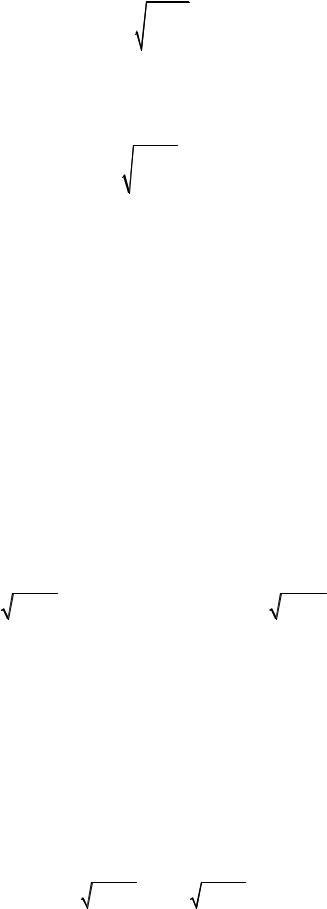
′ |
= |
v2 |
≤ x |
(45.3) |
x |
x 1− c2 |
(Лоренцовое сокращение движущихся масштабов).
2) Промежуток времени между двумя событиями, происходящими в од-
ной точке, связаны условием: |
t |
|
|
|
||
t′ = |
|
≥ |
t, |
(45.4) |
||
|
|
|||||
1 |
− |
v2 |
|
|
||
c2 |
|
|
||||
|
|
|
|
|
||
т.е. движущиеся часы идут медленнее неподвижных.
Существует, однако, определенная комбинация пространственных и временных координат, которая имеет одинаковое значение во всех ИСО, на-
зываемая релятивистским интервалом:
s2 = x2 + y2 + z2 −c2 t2 = x2 + y2 + z2 +(ict )2 = s′2 . |
(45.5) |
Для дальнейшего удобно объединить пространственные и временные координаты в виде 4-х вектора пространства-времени, имеющего компоненты:
x1 = x; x2 = y; x3 = z; x4 = ict. |
(45.6) |
Тогда интервал, будучи квадратом соответствующего 4-х вектора, и, следовательно, релятивистским скаляром, одинаковым во всех ИСО, можно записать как:
|
s2 = x2 + |
x2 + |
x2 |
+ x2 |
= |
r2 − c2 t2 . |
(45.7) |
||||
1 |
|
2 |
3 |
4 |
|
|
|
|
|
||
Из условия (45.1), преобразования Лоренца тогда можно представить в |
|||||||||||
виде (с учетом обозначения β ≡ v ): |
|
|
|
|
|
|
|
||||
|
x1 +iβx4 |
|
c |
|
|
|
|
x1 −iβx4 |
|
|
|
x1′ = |
; |
x2′ = x2 |
; |
x3′ = x3; |
x4′ = |
. |
(45.8) |
||||
|
|
||||||||||
|
1− β2 |
|
|
|
|
|
1− β2 |
|
|||
Обратные преобразования Лоренца (K′→ K ) |
получаются из (45.8) путем |
||||||||||
формальной замены v −v или β −β. |
|
|
|
|
|
|
|||||
Вообще, 4-х вектором |
называется |
набор из 4-х |
параметров |
||||||||
(x1, x2 , x3 , x4 ), который преобразуется |
в соответствии с уравнениями (45.8). |
||||||||||
Тогда, квадрат 4-х вектора, скалярное произведение двух 4-х векторов и т.д. будут являться 4-х мерными скалярами, и следовательно будут инвариантными во всех ИСО.
Полученные преобразования Лоренца позволили построить 4-х мерную динамику, согласно которой, в частности, энергия и импульс свободной частицы имеют вид:
E = |
m c2 |
|
; p = |
m v |
. |
(45.9) |
||
|
0 |
|
0 |
|
||||
1 |
|
|
1− |
β2 |
||||
|
− β2 |
|
|
|||||
|
|
|
125 |
|
|
|
|
|

и 4-х вектор плотности тока (45.17): |
|
|||
|
|
|
k jk = 0 , |
(45.19) |
|
|
∂ |
|
|
где введено обозначение: |
k ≡ |
|
. |
(45.20) |
∂x |
||||
|
|
k |
|
|
Уравнение (45.19) |
полностью эквивалентно уравнениям |
(45.15) и |
||
(45.16), с учетом автоматического суммирования по повторяющимся индексам.
Рассмотрим, наконец, 4-х мерный аналог оператора Лапласа :
|
= |
|
∂ 2 + |
|
∂ 2 + |
∂ 2 = ∑ k2 |
; |
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
|
|
2 |
|
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|||
|
|
|
∂x |
|
|
∂y |
|
|
∂z |
|
k =1 |
|
|
|
|
(45.21) |
||||||||
|
|
|
|
|
∂2 |
|
|
|
∂2 |
|
|
∂2 |
|
|
∂2 |
|
|
1 |
|
∂2 |
||||
|
2 |
= |
|
+ |
|
+ |
+ |
|
= − |
|
≡ . |
|||||||||||||
k |
|
∂x2 |
|
∂x2 |
∂x2 |
|
∂x2 |
c2 |
|
∂t2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
1 |
|
|
2 |
|
|
3 |
|
4 |
|
|
|
|
|
|
||||||
Здесь символом обозначен т.н. оператор Даламбера.
§ 46. Релятивистское уравнение Клейна – Гордона – Фока (КГФ) для бесспиновых микрочастиц
Рассмотрим свободное движение частиц, не обладающих спином. Такие частицы называются скалярными (π-, K- мезоны…).
В нерелятивистском случае связь энергии и импульса имеет вид:
E = |
p2 |
, |
(46.1) |
|
2m |
||||
|
|
|
причем движение частицы описывается волновым УШ:
ih |
∂ψ |
= − |
h2 |
ψ . |
(46.2) |
|
∂t |
2m |
|||||
|
|
|
|
С формальной точки зрения, последнее уравнение можно получить из уравнения (46.1) путем введения операторов:
|
|
|
∂ |
|
|
|
E → E →ih |
; p →p = −ih , |
(46.3) |
||||
|
||||||
|
|
|
∂t |
|
||
и применения их действия к волновой функции ψ . |
|
|||||
Теперь необходимо объединить идеи СТО и квантовой механики. Для |
||||||
этого в основном уравнении (45.14) |
необходимо перейти к операторам: |
|
||||
|
2 |
+ m2c2 = 0 , |
(46.4) |
|||
p |
k |
|||||
|
|
0 |
|
|||
где первые три компоненты оператора импульса определены в (46.3), а четвертая имеет вид:
|
|
|
|
i |
∂ |
|
∂ |
|
∂ |
|
|
||
|
|
E |
|
|
|
. |
(46.5) |
||||||
p4 |
= i |
|
→ |
|
ih |
|
|
= −ih |
|
= −ih |
|
||
c |
|
|
∂(ict ) |
∂x4 |
|||||||||
|
|
|
c |
∂t |
|
|
|
|
|||||
127
|
2 2 |
2 |
1 |
|
∂ |
|
|
|
|
|
|
2 |
|
||
Тогда |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
, и, следовательно, операторное |
|
pk = −h k |
= −h − |
|
|
|
|
|
|
|
= −h |
|
|||||
c |
2 |
|
∂t |
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
уравнение (46.4) примет вид: |
|
|
|
−h2 +m2c2 |
= 0. |
||||||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
Если ввести обозначение: χ |
2 |
= |
m2c2 |
, и применить действие соответст- |
||||||||||
|
|
|
0 |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вующих операторов на волновую функцию ψ , тогда последнее уравнение
можно представить в виде: |
|
) |
|
( |
−χ2 |
(46.6) |
|
|
ψ =0 . |
Уравнение (46.6) является релятивистским волновым уравнением для свободной бесспиновой частицы и называется уравнением Клейна – Гордона – Фока
(КГФ). Это уравнение инвариантно относительно преобразований Лоренца, если ψ – четырехмерная скалярная функция.
Всвязи с уравнением КГФ возникает два вопроса:
1)Так как уравнение КГФ описывает свободное движение частицы, то
всоответствие с постулатом №1, плоская волна де Бройля:
ψ p = Ae |
− |
i |
(Et−p r) |
, |
(46.7) |
|
h |
||||||
|
|
но с релятивистским соотношением (45.10), должна быть решением полученного уравнения.
2) Из уравнения КГФ необходимо получить уравнение непрерывности с положительно определенной плотностью вероятности, с тем, чтобы дать стандартную физическую интерпретацию волновой функции.
Рассмотрим вначале первый вопрос. Для этого подставим выражение (46.7) в уравнение КГФ:
( |
|
2 |
|
|
1 ∂2 |
m2c2 |
− |
i |
(Et−r p) |
|
1 |
|
2 |
|
E2 |
2 |
2 |
|
|
|||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
−χ |
|
)ψ = |
− |
|
|
|
|
|
− |
0 |
2 |
Ae |
|
h |
|
= − |
|
|
p |
|
− |
|
|
+ m0 c |
|
ψ = 0 |
, |
|
|
c |
2 |
|
∂t |
2 |
|
h |
2 |
|
c |
2 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
что является очевидным с учетом условия (45.10).
Получим, наконец, уравнение непрерывности в релятивистском случае. Для этого запишем уравнение КГФ для функций ψ и ψ :
( k2 −χ2)ψ = 0; |
(46.8) |
( k2 −χ2)ψ = 0. |
(46.9) |
Умножив первое уравнение слева на ψ , а второе – на ψ , и, вычитая одно из другого, получим:
ψ 2kψ −ψ 2kψ = k (ψ kψ −ψ kψ )= 0.
128

Для согласования с нерелятивистским случаем, умножим последнее равенст-
во на |
h |
и введя 4-х вектор тока: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
2mi |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
|
= |
|
|
h |
|
ψ ψ −ψ ψ |
) |
, |
k =1,2,3,4, |
(46.10) |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
k |
|
|
2mi ( |
|
|
|
|
k |
|
|
k |
|
|
|
|
|
|
||||||||
получим уравнение непрерывности (45.19): |
|
|
|
|
|
|
(46.11) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k jk |
= 0. |
|
|
|
|
|
|
|
Для плотности тока вероятности (k =1,2,3) получаем такое же уравнение, |
||||||||||||||||||||||||||||||||
как и в нерелятивистском случае: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j = |
h |
|
|
|
ψ ψ −ψ ψ |
) |
. |
(46.12) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2mi |
||||||||||||||||||
|
|
|
|
|
∂ |
|
|
|
1 |
|
|
∂ |
|
|
|
|
|
( |
|
|
|
|
|
|
||||||||
При к = 4 → |
k |
= |
|
= |
|
|
, тогда: |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
∂x |
|
ic ∂t |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
= |
|
h |
|
|
|
1 |
ψ ∂ψ −ψ |
∂ψ |
|
|
= icρ . |
(46.13) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂t |
|
∂t |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
2mi ic |
|
|
|
|
|
|
|
|
|
||||||||||
Отсюда для плотности вероятности получаем: |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ρ = |
|
|
|
ih |
|
|
|
ψ ∂ψ −ψ ∂ψ |
. |
(46.14) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2mc |
|
|
∂t |
|
|
∂t |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Для сравнения с нерелятивистским пределом, воспользуемся заменой: ih∂∂ψt Eψ; −ih∂∂ψt * Eψ .
Тогда, для ρ получаем ρ = mcE 2 ψ ψ , которое при vc n1 и, следовательно,
E ≈ mc2 , приводит к ожидаемому результату: ρ = ψ
 2 .
2 .
Однако, в релятивистском случае выражение (46.14) не является положительно определенной величиной, что противоречит принципиальным положениям квантовой механики.
Другим важным недостатком теории КГФ является невозможность опи-
сания релятивистского электрона с учетом наличия у него спина. Чтобы описать спиновые состояния электрона, его волновая функция должна быть, по крайней мере, двухкомпонентной, в соответствии с теорией Паули (§ 34).
§ 47. Уравнение Дирака
Для решения всех проблем, возникших в теории КГФ, Дирак (1928) предположил, что состояние релятивистского электрона должно описываться линейным дифференциальным уравнением первого порядка, и предложил следующую схему линеаризации уравнения КГФ.
129
Разумеется, будем исходить из уравнения КГФ, так как это уравнение, во-первых, отражает правильную связь между релятивистской энергией и импульсом, во-вторых, является релятивистки инвариантным, в-третьих, допускает правильный предельный переход к нерелятивистскому случаю.
Запишем уравнение КГФ:
|
|
|
|
|
|
|
|
|
|
|
( −χ2)ψ = 0, |
|
|
|
(47.1) |
где |
= |
2 |
= |
2 |
+ |
2 |
+ |
2 |
+ |
2 |
– оператор Даламбера, χ |
2 |
= |
m2c2 |
|
k |
|
2 |
3 |
4 |
|
0 |
. Оператор в ле- |
||||||||
|
|
1 |
|
|
|
|
|
|
h2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
вой части уравнения КГФ запишем в виде:
( |
2 |
$ |
$ |
+χ), |
(47.2) |
−χ ) = (γ k k |
−χ) (γ l l |
||||
где k,l =1,2,3,4; по повторяющимся индексам (которые называются “немы-
ми”) предполагается суммирование; γ$k – некоторые неизвестные операторы,
которые, по предположению, не действуют на пространственно-временные переменны xk . Тогда, в частности, эти операторы коммутируют с операто-
рами k .
Найдем условия, которым должны удовлетворять операторы γ$k . Для
этого обратимся к уравнениям (47.2), которые справедливы, если:
= 2k =γ$k γ$l k l = 12 (γ$k γ$l k l +γ$l γ$k l k )= 12 (γ$k γ$l +γ$l γ$k ) k l .
Здесь мы учли, что операторы дифференцирования k и l коммутируют
между собой, а также с операторами γ$k . Очевидно, последнее условие справедливо, если выполняются коммутационные соотношения вида:
|
γ$k γ$l + γ$l γ$k |
= 2δ kl , |
(47.3) |
||
т.е. эти операторы между собой антикоммутируют: |
|
||||
γ$k |
γ$l + γ$l γ$k |
= 0, |
(k ≠ l ); |
(47.4) |
|
γ$k2 |
= 1, |
(k = l ). |
|||
|
|||||
Заметим, что в последнем равенстве отсутствует суммирование по к. Ранее было показано (§ 34), что полученным коммутационным соотно-
шениям удовлетворяют 2-х рядные матрицы Паули σα (α =1,2,3):
|
|
0 |
1 |
; |
|
|
0 −i |
|
|
|
1 |
0 |
|
|||||
σ1 |
=σ x = |
1 |
0 |
|
σ 2 |
=σ y = |
0 |
|
; |
σ 3 |
=σ z = |
0 |
. |
|||||
|
|
|
|
|
|
|
i |
|
|
|
|
|
−1 |
(47.5) |
||||
Поэтому, естественно предположить, что искомые операторы также являются матрицами, удовлетворяющие соотношениям (47.4). Однако, таких матриц должно быть не 3, а по меньшей мере 4, что непосредственно следует из условий (47.3). Простые соображения показывают, что и размерность этих матриц также должно равняться четырем. Имеется несколько альтернативных
130
