с.м.чернов_квантовая механика

Интересно отметить, что указанная производная определяется не только

свойствами оператора F , но зависит от особенностей силового поля U (r,t ),

входящего в оператор H .

Полученный результат (18.3) позволяет сформулировать общий критерий, когда физическая величина сохраняется во времени (является интегралом

1) ∂F = 0, то есть, оператор явно от времени не зависит.

∂t

F

§ 19. Стационарные состояния. Стационарное уравнение Шредингера

Пусть микрочастица движется в силовом поле, где потенциальная энергия частицы U (r) не зависит от времени. Такие поля называются стационар-

ными. В этом случае оператор H также от времени не зависит. Тем не менее, динамика движения частицы описывается общим УШ:

∂Ψ (r , t ) = Ψ ( ) . (19.1)

ih H r , t

∂t

Сматематической точки зрения, уравнение (19.1) является дифференциальным уравнением в частных производных. В нашем случае его можно решить методом разделения переменных. Для этого представим волновую функцию в виде:

Ψ(r,t )= A(t ) f (r). (19.2)

41

Подставляя решение (19.2) в уравнение (19.1), и разделив полученный результат на функцию ψ (r,t ), получим соотношение:

В последнем уравнении левая часть зависит только от t, а правая лишь от r . Причем, равенство выполняется при всех значениях независимых пере-

менных r и t, но это возможно лишь тогда, когда левые и правые части равны постоянной Е. Тогда мы получаем два независимых уравнения для временной

Отсюда следует, что временная зависимость волновой функции являет-

ся универсальной функцией и не зависит от потенциала U (r). Особенность силового поля определяет лишь координатную часть волновой функции f (r)

в соответствии с уравнением (19.5). Из этого уравнения можно определить также физический смысл постоянной разделения Е. Так как E является собст-

венным значением гамильтониана, то она имеет смысл полной энергии частицы в заданном силовом поле. Уравнение (19.5) является основным уравнением квантовой механики при решении стационарных задач и называется

Не сложно получить решение уравнения (19.4) методом разделения переменных:

где f (r) является решением стационарного УШ (19.5).

Важно заметить, что, хотя волновая функция и зависит явно от t, однако, все

наблюдаемые параметры являются стационарными, например, плотность вероятности и плотность тока вероятности определяются лишь координатной волновой функцией:

ГЛАВА III

Точно решаемые задачи квантовой механики

§ 20. Общие свойства одномерного движения

Пусть частица массы m движется в стационарном одномерном поле

U (x). В.ф. для любого стационарного поля имеет вид:

−i Et

ψ (x,t)= e h ψ (x), (20.1)

где координатная часть ψ (x) является решением стационарного одномерного УШ вида

При этом в.ф. должна удовлетворять “стандартным” условиям:

1)Однозначности.

2)Конечности.

3)Непрерывности ψ .

4) Непрерывности ψ ′ = ddxψ (если потенциальная энергия не испытывает

бесконечных скачков).

Первые три требования непосредственно связаны с физическим смыслом в.ф. ψ (x). Однако, четвертое условие является следствием УШ.

Рассмотрим, например, потенциал, имеющий конечный скачок U0 в точке x = a . УШ (20.2) запишем в виде:

d 2ψ (x) = − 2m E −U (x) ψ (x)≡ f (x). dx2 h2

Интегрируя последнее уравнение в окрестности точки a , и используя

теорему о среднем, получаем:

При конечном f (a′) и c → b имеем: ψ′(c)=ψ′(b).

Однако в случае бесконечного скачка потенциала это равенство нару-

шается и производная ψ′(x) может испытывать скачок.

Укажем некоторые достаточно общие свойства одномерного движения для некоторого класса силовых полей U (x).

Теорема 1. В одномерных задачах все энергетические уровни дискретного спектра не вырождены.

43

Таким образом, при симметричной потенциальной энергии в.ф. стацио-

нарного состояния может быть либо четной, либо нечетной. В частности, для

основного состояния в ф. не имеет узлов и должна быть всегда четной функцией х. Нечетные решения всегда должны иметь узел при х=0,

ψ неч (0 ) = 0 , т.к. ψ (0) = −ψ (0) = 0 .

Теорема 4. Пусть частица движется в одномерном периодическом по-

образом, в любом периодическом поле волновая функция должна удовлетворять условию:

Проверим, что уравнение (20.11) эквивалентно условию (20.10). Действительно:

ψ (x + a)= A(x + a)eik(x+a) = A(x)eikxeika = eikaψ (x).

Волновая функция (20.11) называется в.ф. Блоха (1928).

45

Для свободного пространства в.ф. Блоха совпадает с плоской волной де Бройля ψ (x)= A0eikx , а есть импульс свободной частицы. В периодическом поле, однако, волновое число k определяется неоднозначно, т.к. при замене k → k′+ 2πan мы получаем ту же в.ф., удовлетворяющую условию (20.10).

Действительно: ψ (x +a)= eik′aψ (x)= eikaψ (x)ei2πn = eikaψ (x).

То есть импульсы и p′ = hk′ также является физически эквивалентными. Поэтому p = hk в периодическом поле называют квазиимпульсом.

§ 21. Движение частицы в прямоугольной потенциальной яме

Известно, что в случае бесконечно глубокой потенциальной ямы ширины 2а частица имеет дискретные уровни энергии вида:

En = π2h2 n2 ( n =1, 2…). (21.1)

8ma2

Рассмотрим аналогичную задачу для более реалистичного случая ямы конечной глубины U0 . Пусть частица массы m движется в одномерном ста-

ционарном поле вида:

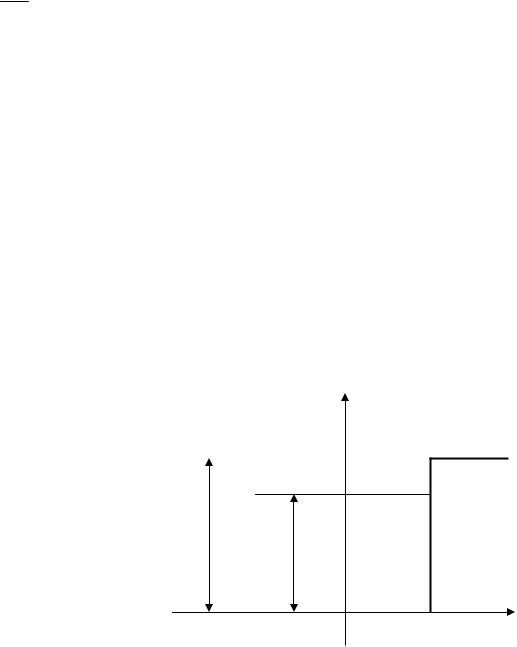
U(x)

Рис. 4. Модель прямоугольной ямы ширины 2а и глубины U0

При этом ограничимся случаем E<U0 .

Так как силовое поле является четной функцией координаты х, то решение УШ должно также обладать определенной четностью.

Движение частицы в таком поле описывает УШ:

46

Частными решениями уравнения (21.3) являются функции e±æx .

Чтобы решения удовлетворяли стандартному условию ограниченности, можно взять решения в виде:

Для нахождения уровней энергии Е, которые входят в k и æ, необходимо обратиться к оставшимся стандартным условиям. Полученные решения ψ1,ψ2 и ψ3 являются конечными, однозначными, непрерывными и имеют не-

прерывные производные везде, кроме граничных точек x = ±a . Поэтому осталось «сшить» решения в этих точках. В силу симметрии поля достаточно рассмотреть эти условия лишь в одной точке x=a:

Полученные уравнения можно исследовать графически. Умножая эти уравнения на а и вводя обозначения для безразмерных величин:

47

уравнения (21.10) и (21.11) принимают вид:

Заметим, что α и β зависят от Е, однако сумма их квадратов от Е не зависит:

α2 + β2 = a2 (k 2 +Q2 ) = 2m U0a2 ,

h2

так что на плоскости (α , β ) это уравнение есть уравнение окружности

1

R = 2mU20a2 2 . (21.14б)

h

Таким образом, нахождение энергии частицы в яме сводится к совместному решению системы уравнений (21.13) и (21.14). Заметим, что все расчеты чувствительны к характерной комбинации U0a2 . Поэтому для иллюстрации

рассмотрим 3 частных случая:

ственный четный уровень. Во втором случае R = R2 = 2 имеется один четный

48

и один нечетный уровень. В третьем случае R = R3 = 4 имеется два четных и

Объединяя четные и нечетные решения, мы получим результат, совпадающий

с решениями (21.1) для n =1,2,3,4,...

Замечание. Модель металлов по Зоммерфельду.

Решенная задача может служить иллюстрацией одномерной модели металла, находящегося при абсолютном нуле температуры. Движение свободных электронов в металлах, выход которых наружу затруднен из-за притяжения ионов кристаллической решетки, можно представить как движение электронов внутри потенциальной ямы глубины U0 , ширина которой совпадает с

размерами металла. В соответствии с принципом минимума энергии и принципом запрета Паули электроны занимают все нижние уровни энергии до мак-

может принимать непрерывный ряд значений из интервала [0,∞]. В теории Планка осциллятор имеет дискретный набор уровней

Рассмотрим свойства осциллятора с точки зрения квантовой механики. Укажем вначале свойства осциллятора, следующие из общей теории (§20):

49

1. Так как движение частицы финитное, то уровни энергии En должны

быть дискретными.

2. Так как задача одномерная, то все дискретные уровни – не вырож-

денные.

3. В.ф. осциллятора, в соответствии с осцилляционной теоремой, должна иметь (n −1)узлов.

4. Так как U (x) – четная функция х, то в.ф. должна обладать опреде-

ленной четностью.

Динамика движения квантового осциллятора описывается одномерным стационарным уравнением Шредингера, которое мы запишем в виде:

Для дальнейшего, введем безразмерные величины:

Математическое решение последнего уравнения приведем в конце данного параграфа. Здесь укажем лишь окончательные результаты. Решения уравнения (22.7), удовлетворяющие стандартным условиям, существуют, если выполняется условие: λ = 2n +1, где n = 0,1,2,… Тогда, с учетом обозначения

(22.6), находим уровни энергии квантового осциллятора:

где нормировочная постоянная Аn равна:

Hn (ρ) – полиномы n -ой степени, которые в математической литературе на-

зываются полиномами Чебышева-Эрмита. Укажем некоторые свойства этих полиномов. В общем случае, любой полином можно представить в виде про-

изводящей функции: